一、问题求解下列每题给出的A、B、C、D、E五个选项中,只有一项是符合试题要求的.
5. 已知a,b,c为正数,若方程ax
2+bx+c=0有两个不等实根,则方程a
2x
2+b
2x+c
2=0______.
- A.有两个不等正根
- B.有两个不等负根
- C.有一个正根一个负根
- D.未必有实根
- E.有一个零根
A B C D E
B
[解析] 由已知条件,有b
2-4ac>0.且a,b,c为正数.所以,有b
4≥16a
2c
2>4a
2c
2.从而,方程a
2x
2+b
2x+c
2=0有两个不等实根x
1,x
2,又
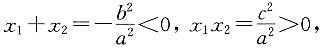
可知x
1,x
2均为方程的负根.
故本题应选B.
13. 甲、乙、丙依次轮流投掷一枚均匀的硬币,若先投出正面者为胜,则甲获胜的概率是______.
A.
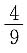
B.
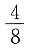
C.
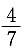
D.
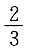
E.
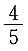
A B C D E
C
[解析] 设A
i=(第i次甲投出正面);B
i={第i次乙投出正面};C
i={第i次丙投出正面}(i=1,2,…).则
P(甲获胜)=
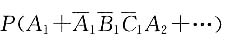
等式右端中,相加的各事件互不相容,每一项中相乘的各事件相互独立,所以

故本题应选C.
14. 把一个木制的正方体加工成尽可能大的球,那么球的体积与正方体体积的比为______.
- A.6:π
- B.8:π
- C.π:8
- D.π:6
- E.π:3
A B C D E
D
[解析] 设正方体的棱长为a,其体积V
1=a
3.
由题意,球的半径r应是正方体棱长的一半,即
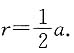
球的体积
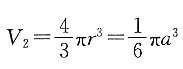
所以,V
2:V
1=π:6.
故本题应选D.
二、条件充分性判断要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论.A、B、C、D、E五个选项为判断结果,请选择一项符合试题要求的判断.
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
6.
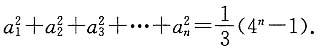
(1)数列{a
n}的通项公式为a
n=2
n (2)在数列{a
n}中,对任意正整数n,有a
1+a
2+a
3+…+a
n=2
n-1
A B C D E
B
[解析] 由条件(1),a
n=2
n,则
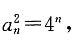
所以
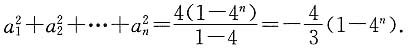
条件(1)不充分.
由条件(2),S
n=2
n-1,而a
n-S
n=S
n-1=2
n-1.
所以,
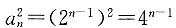
,于是
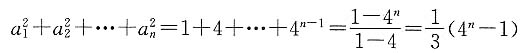
故条件(2)充分.
故本题应选B.
7. 对任意实数x,有ax
2+(a-1)x+n-1<0.
(1)
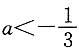
(2)a>1
A B C D E
A
[解析] 设f(x)=ax
2+(a-1)x+a-1.由条件(1),
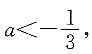
f(x)的图象是开口向下的抛物线,要使得f(x)<0对任意x成立,只需判别式
Δ=(a-1)
2-4a(a-1)<0
即3a
2-2a-1>0,解得
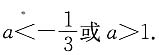
由此可知条件(1)充分.
由条件(2),a>1>0,f(x)的图象是开口向上的抛物线.a>1时,始终有f(x)>0,条件(2)不充分.
故本题应选A.
9. x
3+y
3+3xy=1.
(1)x+y=1
(2)
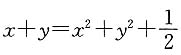
A B C D E
D
[解析] 由条件(1),x+y=1,所以
x
3+y
3+3xy=(x+y)(x
2-xy+y
2)+3xy=x
2+2xy+y
2=(x+y)
2=1
所以,条件(1)充分.
由条件(2),
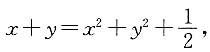
改写为
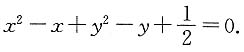
即
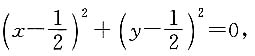
所以
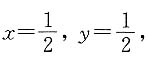
可见
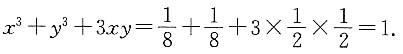
条件(2)也充分.
故本题应选D.
10. 直线x-y=k与圆y
2=-x
2+4没有交点.
(1)k>5
(2)
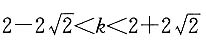
A B C D E
A
[解析] 圆的方程可写成(x-2)
2+y
2=4.圆心C(2,0)到直线x-y-k=0的距离
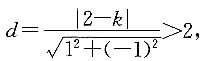
则直线与圆无交点.解不等式
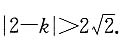
可得
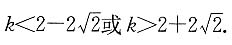
由条件(1),
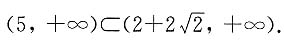
所以条件(1)充分,而条件(2)不充分.
故本题应选A.
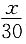 吨,由题意,有
吨,由题意,有
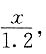 若记女生人数为a,则男生人数为1.8a,则全班测验的总分为2.8a×75,得
若记女生人数为a,则男生人数为1.8a,则全班测验的总分为2.8a×75,得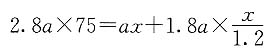
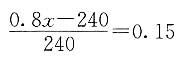
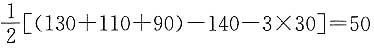
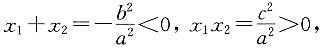 可知x1,x2均为方程的负根.
可知x1,x2均为方程的负根.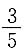 ,则甲、乙两地的公路长为______.
,则甲、乙两地的公路长为______.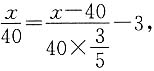 解得x=280(公里).
解得x=280(公里).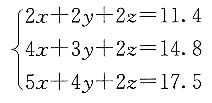
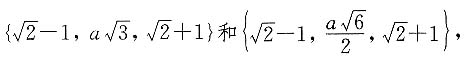 则使前者成为等差数列,后者成为等比数列的实数a的值有______.
则使前者成为等差数列,后者成为等比数列的实数a的值有______.
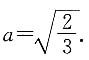
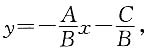 因为AB<0,BC<0.可知直线斜率
因为AB<0,BC<0.可知直线斜率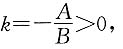 直线在y轴上的截距
直线在y轴上的截距 所以此直线必过Ⅰ、Ⅱ、Ⅲ象限.
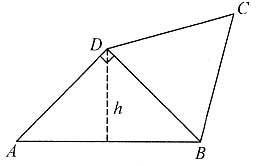
所以此直线必过Ⅰ、Ⅱ、Ⅲ象限.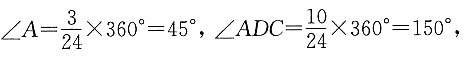 而∠CDB=60°,所以∠ADB=90°,△ADB为等腰直角三角形,又AB=8,所以AB边上的高h=4,△ADB面积=
而∠CDB=60°,所以∠ADB=90°,△ADB为等腰直角三角形,又AB=8,所以AB边上的高h=4,△ADB面积=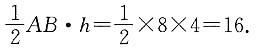
 .
.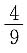
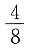
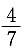
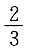
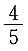
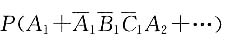

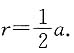 球的体积
球的体积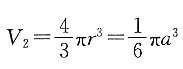
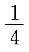

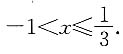
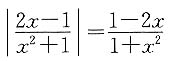
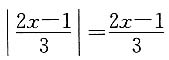
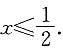 条件(1)不充分.
条件(1)不充分.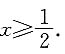 条件(2)不充分.
条件(2)不充分. 也不充分.
也不充分.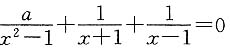 有实根.
有实根.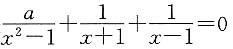 两边同乘x2-1,并化简得2x+a=0,
两边同乘x2-1,并化简得2x+a=0,
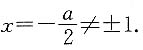 方程有实根.
方程有实根.

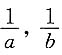 的算术平均值为n
的算术平均值为n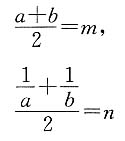
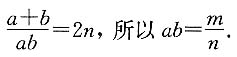
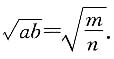 故本题应选C.
故本题应选C.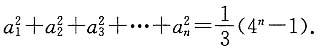
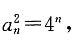 所以
所以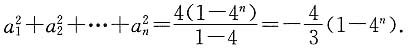 条件(1)不充分.
条件(1)不充分.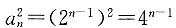 ,于是
,于是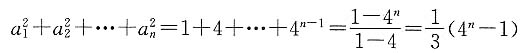
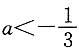
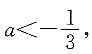 f(x)的图象是开口向下的抛物线,要使得f(x)<0对任意x成立,只需判别式
f(x)的图象是开口向下的抛物线,要使得f(x)<0对任意x成立,只需判别式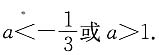 由此可知条件(1)充分.
由此可知条件(1)充分.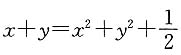
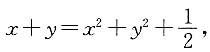 改写为
改写为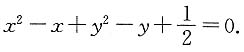 即
即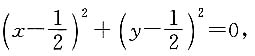 所以
所以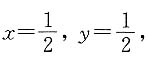 可见
可见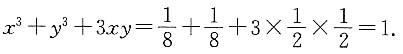 条件(2)也充分.
条件(2)也充分.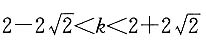
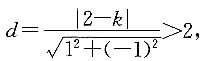 则直线与圆无交点.解不等式
则直线与圆无交点.解不等式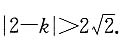 可得
可得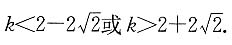
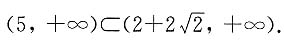 所以条件(1)充分,而条件(2)不充分.
所以条件(1)充分,而条件(2)不充分.