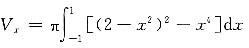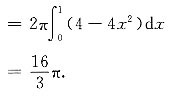银符考试题库B12
现在是：
试卷总分：100.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
高等数学一自考题模拟25
第Ⅰ部分 选择题
一、单项选择题
(在每小题列出的四个备选项中只有一个是符合题目要求的．)
1. 函数
的定义域是______
A.(-2，3]
B.[-3，3]
C.(-2，-1)和(-1，3]
D.(-3，-2)和(-2，3)
A
B
C
D
C
[考点] 本题主要考查的知识点是函数的定义域．
[解析] 根据定义域原则中的分式分母不得为零，偶次根式被开方式大于或等于零，对数的真数大于零等，有
-2＜x＜-1，-1＜x≤3，故其定义域为(-2，-1)和(-1，3]．
2.
______
A.1
B.∞
C.-1
D.0
A
B
C
D
D
[考点] 本题主要考查的知识点是利用等价无穷小量求极限．
[解析]
3. 设f(x)为可导函数，且
，则f
'
(x
0
)=______
A．1
B．0
C．2
D．
A
B
C
D
C
[考点] 本题主要考查的知识点是函数在某一点处的导数的定义．
[解析] 由导数定义可知
而
所以
4. 曲线y=xe
-x
的拐点是______
A.(1，e
-1
)
B.(2，2e
-2
)
C.(3，3e
-3
)
D.(4，4e
-4
)
A
B
C
D
B
[考点] 本题主要考查的知识点事函数的拐点．
[解析] 因为y=xe
-x
，所以y
'
=e
-x
-xe
-x
．y
"
=-e
-x
-(e
-x
-xe
-x
)=(-1-1+x)e
-x
=(x-2)e
-x
．
令y
"
=(x-2)e
-x
=0解得x=2．
又因为当x＞2时，y
"
＞0，曲线是凹的，当x＜2时，y
"
＜0．曲线是凸的，则曲线y=xe
-x
的拐点是(2，2e
-2
)．
5. 设某商品的市场需求函数为
，p为商品价格，则需求弹性函数为______
A．
B．
C．
D．
A
B
C
D
C
[考点] 本题主要考查的知识点是需求弹性．
[解析] 因为需求弹性函数为
，又因为
则所求为
6. 微分方程(xlnx)y
'
=y的通解是______
A．y=Clnx
B．
C．y=Cln(x+1)
D．
A
B
C
D
A
[考点] 本题主要考查的知识点是可分离变量微分方程的通解．
[解析] 该方程可变形为
两边积分得lny=ln(lnx)+C
1
，所以y=Clnx．
7. 定积分
的值是______
A．
B．
C．
D．3
A
B
C
D
C
8.
______
A．2
B．3
C．
D．
A
B
C
D
D
9. 设z=e
-sin
2
xy
2
，则
______
A.-2xysin(2xy
2
)e
-sin
2
xy
2
B.2xysin(2xy
2
)e
-sin
2
xy
2
C.2xy
2
sin(2xy
2
)e
-sin
2
xy
2
D.-2xy
2
sin(2xy
2
)e
-sin
2
xy
2
A
B
C
D
A
[考点] 本题主要考查的知识点是偏导数．
[解析]
=-2e
-sin
2
xy
2
·sinxy
2
·(sinxy
2
)
y
'
=-2e
-sin
2
xy
2
·sinxy
2
·cosxy
2
·(xy
2
)
y
'
=-sin(2xy
2
)e
-sin
2
xy
2
·2xy
=-2xysin(2xy
2
)e
-sin
2
xy
2
．
10. 设积分区域D是2≤x
2
+y
2
≤4，则
______
A．8π
B．4π
C．2π
D．
A
B
C
D
C
[考点] 本题主要考查的知识点是二重积分的性质．
[解析] 当被积函数是1时，二重积分的值是被积区域的面积，即
第Ⅱ部分 非选择题
二、简单计算题
(每小题4分，共20分)
1. 求极限
解：
2. 设
当a取什么值时，函数f(x)在其定义域内连续?
解：f(x)在x≠3时是连续函数，因此f(x)只要在x=3处连续，就在其定义域内连续．因为
，f(3)=a，所以只要a=6，f(x)就在其定义域内连续．
3. 设
，求
．
解：方程两边对x求导得
4. 计算定积分
解：
当x=-1，1时，u=3，1．
5. 设
，且f可微，求dz．
解：
所以
三、计算题
(每小题5分，共25分)
1. 求函数
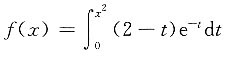
的最大值与最小值．
解：f(x)是偶函数，只考虑在区间[0，+∞)上的情况即可．
f
'
(x)=2x(2-x
2
)e
-x
2
，令f
'
(x)=0，得
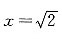
∈(0，+∞)．由于
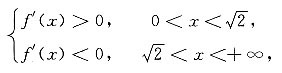
所以
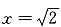
是f(x)在(0，+∞)内的唯一极大值点，而
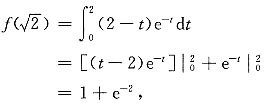
又
，即
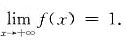
．而且f(0)=0，所以
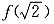
是f(x)在[0，+∞]上的最大值，f(0)是f(x)在[0，+∞)上的最小值．
由于f(x)是偶函数，所以f(x)在(-∞，+∞)内的最大值为1+e
-2
，最小值为0．
2. 求函数f(x)，使
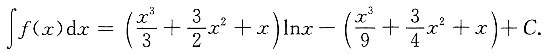
解：因为
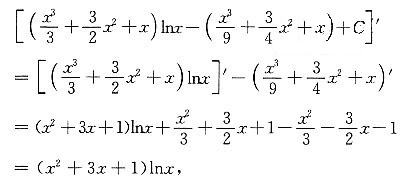
所以f(x)=∫(x)dx=(x
2
+3x+1)lnx．
3. 求不定积分
的值．
解：
4. 求方程
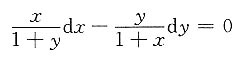
满足初始条件y|
x=0
=1的特解．
解：由
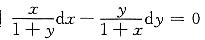
得
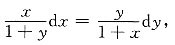
(1+y)ydy=(1+x)xdx，
方程两边积分得
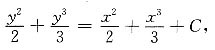
将x=0，y=1代入，得
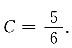
所以，所求特解为3y
2
+2y
3
=3x
2
+2x
3
+5．
5. 求
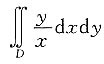
，其中D是由双曲线xy=1及直线y=x，x=2所围成的区域．
解：
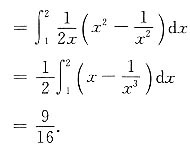
四、综合题
(前三个题，每题6分，第四个题7分，共25分)
1. 要做一个容积为V的圆柱形容器(有盖)，问此圆柱形的底面半径r和高h分别为多少时，所用材料最省?
解：因为πr
2
h=V，所以
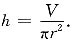
设所用材料为S，则
令S
'
=0得唯一驻点
故当
时所用材料最省．
已知某商品的需求函数是x=125-5p(其中x为产量，p为价格)，总成本函数是C=100+x+x
2
，且生产的商品能全部出售，求：
2. 使利润最大时的产量；
解：收益函数为R=xp=
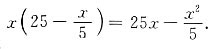
利润函数为
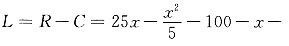
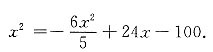
令L
'
=0，即
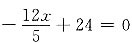
，得x=10．
又
，故当x=10时，L取极大值，由极大值的唯一性知当x=10时，L取最大值，故使利润最大的产量为10．
3. 当利润最大时，商品的需求弹性及商品的售价．
解：当x=10时，商品价格p
商品的需求弹性
已知曲线y=x
2
，求
4. 曲线上当x=1时的切线方程．
解：y=x
2
在x=1处的切点为(1，1)．
切线斜率为
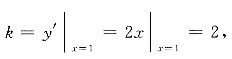
切线方程为y-1=2(x-1)，
即y=2x-1．
5. 求曲线y=x
2
与此切线及x轴所围成的平面图形的面积．
解：所求面积
设由抛物线y=x
2
与y=2-x
2
所围成的平面图形，试求：
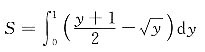
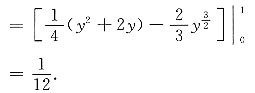
6. 此平面图形的面积．
解：先求两抛物线的交点，得(1，1)，(-1，1)．
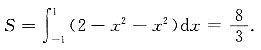
7. 此平面图形绕x轴旋转而成的旋转体的体积．
解：
第Ⅰ部分 选择题
一、单项选择题
1
2
3
4
5
6
7
8
9
10
第Ⅱ部分 非选择题
二、简单计算题
1
2
3
4
5
三、计算题
1
2
3
4
5
四、综合题
1
2
3
4
5
6
7
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
的定义域是______
-2＜x＜-1，-1＜x≤3，故其定义域为(-2，-1)和(-1，3]．
______
，则f'(x0)=______
而
所以
，p为商品价格，则需求弹性函数为______
，又因为
则所求为
两边积分得lny=ln(lnx)+C1，所以y=Clnx．
的值是______
______
______
______
当a取什么值时，函数f(x)在其定义域内连续?
，f(3)=a，所以只要a=6，f(x)就在其定义域内连续．
，求
．
，且f可微，求dz．
的最大值与最小值．
∈(0，+∞)．由于
是f(x)在(0，+∞)内的唯一极大值点，而
，即
．而且f(0)=0，所以
是f(x)在[0，+∞]上的最大值，f(0)是f(x)在[0，+∞)上的最小值．
的值．
满足初始条件y|x=0=1的特解．
得
，其中D是由双曲线xy=1及直线y=x，x=2所围成的区域．
时所用材料最省．
，得x=10．
，故当x=10时，L取极大值，由极大值的唯一性知当x=10时，L取最大值，故使利润最大的产量为10．
深色：已答题 浅色：未答题