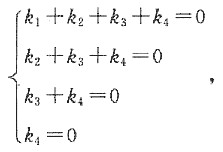一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的.)1. 设向量组α
1,α
2,α
3线性无关,若b
1=3α
1-α
2+α
3,b
2=2α
1+α
2-α
3,b
3=α
1+tα
2+2α
3线性相关,则t应满足的条件是______
A B C D
C
[考点] 本题主要考查的知识点为向量组线性相关的条件.
[解析] 向量组b
1,b
2,b
3线性相关,则

=5(t+2)=0,故t=-2.
3. 设矩阵
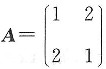
,则在实数域上与A合同的矩阵为______
A.
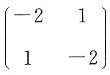
B.
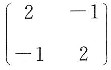
C.
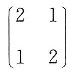
D.
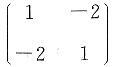
A B C D
D
[考点] 本题主要考查的知识点为合同矩阵的判定.
[解析] 矩阵A是实对称矩阵,特征值为-1、3,故A合同于对角矩阵
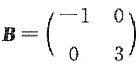
,而选项中各个对称矩阵与对角矩阵B合同的只有选项D.
二、填空题1. 已知二阶方阵A的特征值为λ
1=2,λ
2=-3,则det(A
2)=______.
36
[考点] 本题主要考查的知识点为矩阵特征值的性质.
[解析] 由特征值的性质知A2的全部特征值为4,9,故det(A2)=4×9=36.
2. 设
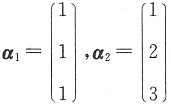
是三元线性方程组Ax=b(b≠0)的解,且r(A)=2,则Ax=b的通解为______.
[考点] 本题主要考查的知识点为非齐次线性方程组解的结构.
[解析] 因为r(A)=2,其基础解系所含解向量的个数是1,而ξ=α2-α1是它的导出组Ax=0的解,且α1,α2都可以作为特解,故本题中非齐次线性方程组的通解可以是α1+k(α2-α1)或者是α2+k(α2-α1).
3. 已知行列式
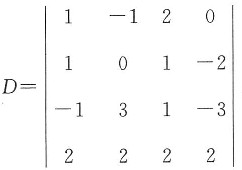
,则 A
11+A
12+A
13+A
14=______.
0
[考点] 本题主要考查的知识点为行列式按某行(列)展开的性质.
[解析] A
11+A
12+A
13+A
14=1×A
11+1×A
12+1×A
13+1×A
14=

4. 设矩阵A
4×3≠0,但AB=0,其中

,则矩阵A的秩r(A)=______.
1
[考点] 本题主要考查的知识点为齐次线性方程组解的结构.
[解析] 因AB=0,所以B的两个列向量都是齐次线性方程组Ax=0的解,而B的两个列向量是线性无关的,故Ax=0的基础解系中至少含2个向量,而基础解系中所含向量的个数为n-r(A)=3-r(A),所以3-r(A)≥2,即r(A)≤1,另外A
4×3≠0
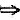
r(A)≥1,故r(A)=1.
5. 设
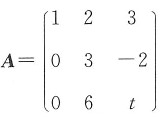
,当t=______时,r(A)=2.
-4
[考点] 本题主要考查的知识点为矩阵的秩.
[解析]
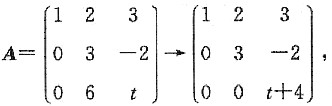
故当t=-4时,r(A)=2.
6. 已知矩阵

,则r(A)=______.
2
[考点] 本题主要考查的知识点为矩阵的秩.
[解析]
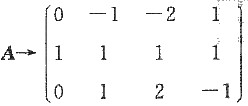
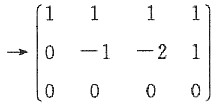
,故r(A)=2.
7. 设n阶实对称矩阵A的特征值分别为1,2,…,n,则当t______时,tE-A是正定的.
t>n
[考点] 本题主要考查的知识点为矩阵正定的条件.
[解析] tE-A的特征值为t-1,t-2,…,t-n,若tE-A是正定的,则t-1>0,t-2>0,…,t-n>0,所以当t>n时,tE-A是正定的.
8. A、B为三阶矩阵,|A|=-1,|B|=2,则|2(A
TB
-1)
2|=______.
2
[考点] 本题主要考查的知识点为矩阵的运算性质与行列式的性质.
[解析] |2(ATB-1)2|=23|(ATB-1)2|=23|ATB-1ATB-1|=23|ATB-1||ATB-1|=23|A|2·(|B-1|)2=23(|B|)-2=2.
9. 若n阶实矩阵A是正交矩阵,即A
TA=E,则|A|=______.
1或-1
[考点] 本题主要考查的知识点为正交矩阵的定义.
[解析] A
TA=E

|A
TA|=|A
T||A|=|A|
2=1
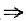
|A|=1或-1.
10. 已知
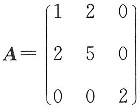
,则A
-1=______.
[考点] 本题主要考查的知识点为分块矩阵的逆矩阵.
[解析]
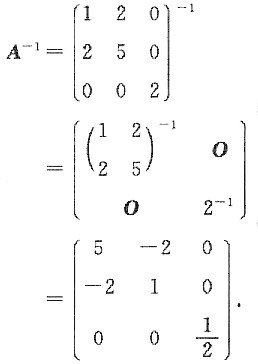
三、计算题(每小题9分,共63分)1. 已知二次型
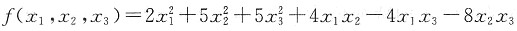
,用正交变换化f(x
1,x
2,x
3)为标准形,并求出其正交变换矩阵Q.

4x
1x
2-4x
1x
3-8x
2x
3,
f的矩阵
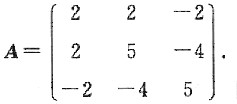
A的特征多项式φ(λ)=(λ-1)
2(λ-10),
于是得到A的特征值为λ
1=λ
2=1,λ
3=10.
对于特征值λ
1=λ
2=1,由方程组(E-A)x=0,
得到属于特征值λ
1=λ
2=1的两个正交的特征向量为
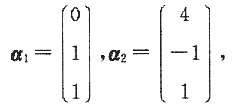
单位化得
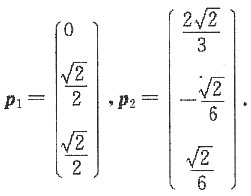
对于特征值λ
3=10,由方程组(10E-A)x=0,得到属于特征值λ
3=10的特征向量为
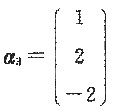
,单位化得
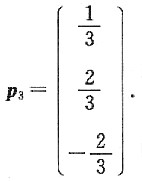
令
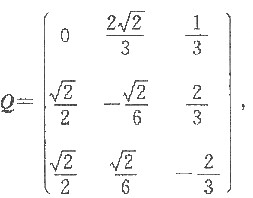
则Q为正交矩阵,且
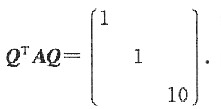
于是作正交变换x=Qy,则有
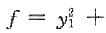
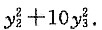
[考点] 本题主要考查的知识点为用正交变换化二次型为标准形.
2. 计算行列式
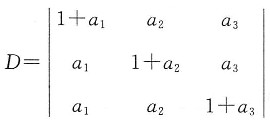
D=
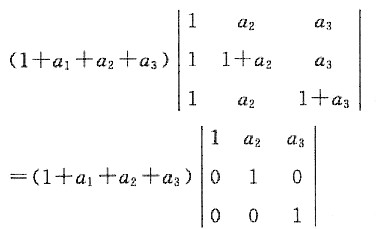
=1+a
1+a
2+a
3.
[考点] 本题主要考查的知识点为行列式的性质.
3. 设A,B满足ABA=2BA-E,其中
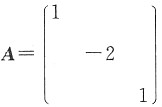
,求B.
将ABA=2BA-E两端右乘A
-1得AB=2B-A
-1,所以(A-2E)B=-A
-1.
即有B=-(A-2E)
-1A
-1
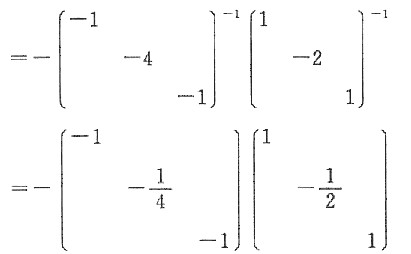
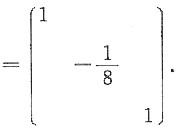
[考点] 本题主要考查的知识点为求解矩阵等式.
4. 已知
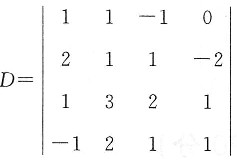
,求A
21+A
22+A
23+A
24.
A
21+A
22+A
23+A
24=
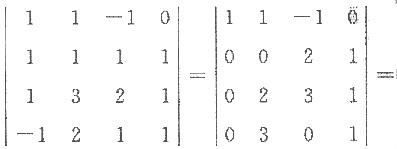
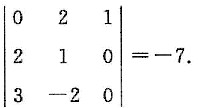
[考点] 本题主要考查的知识点为行列式按一行(或一列)展开的定理.
5. λ为何值时,线性方程组
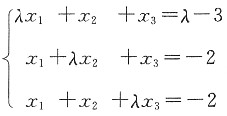
,有唯一解,无解和有无穷多解?当方程组有无穷多解时求其通解.
线性方程组的增广矩阵
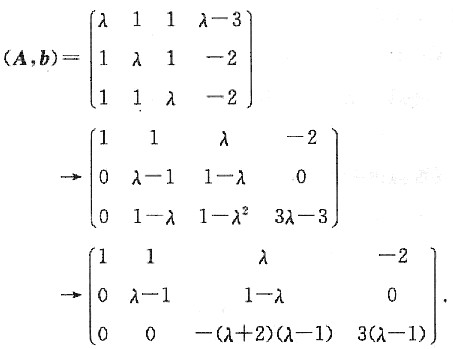
所以,当λ≠1且λ≠-2时,r(A)=r(A,b)=3,
方程组有唯一解;
当λ=-2时,r(A)=2,r(A,b)=3,方程组无解;
当λ=1时,r(A)=r(A,b)=1,方程组有无穷多组解.
当方程组有无穷多解时,同解方程组为
x
1=-x
2-x
3-2,
令x
2=x
3=0,得x
1=-2,从而得到方程组的一个特解
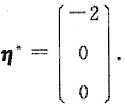
原方程组的导出组的同解方程组为
x
1=-x
2-x
3,
设自由未知量分别取值
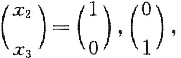
得导出组的基础解系为
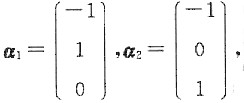
所以原方程组的通解为
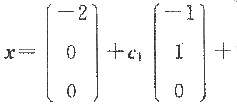
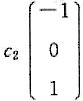
(c
1,c
2为任意常数).
[考点] 本题主要考查的知识点为非齐次线性方程组解的判定.
6. 求矩阵

的秩和列向量组的极大无关组,并用其表示向量组中其余向量.
设A=(α
1,α
2,α
3,α
4),
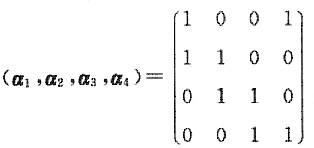
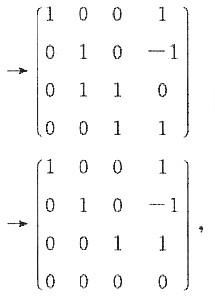
所以r(A)=3,α
1,α
2,α
3为向量组的一个极大无关组,且α
4=α
1-α
2+α
3.
[考点] 本题主要考查的知识点为矩阵的秩与向量组的极大无关组.
7. 设
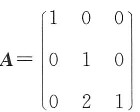
,求A的特征值及其对应的特征向量.
矩阵A的特征多项式为
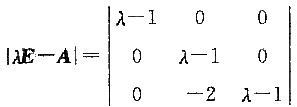
=(λ-1)
3=0,
得特征值λ
1=λ
2=λ
3=1.
对于特征值λ
1=λ
2=λ
3=1,解齐次线性方程组(E-A)x=0.即
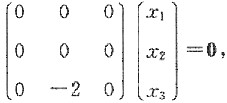
求得基础解系
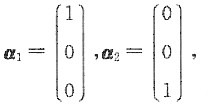
所以矩阵A属于特征值1的全部特征向量为
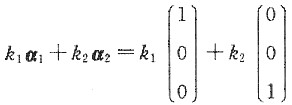
,其中k
1,k
2是不全为零的任意常数.
[考点] 本题主要考查的知识点为矩阵的特征值与特征向量.
四、证明题(本题7分)1. 设β
1=α
1,β
2=α
1+α
2,β
3=α
1+α
2+α
3,β
4=α
1+α
2+α
3+α
4,且向量组α1,α2,α3,α4线性无关,证明:向量组β
1,β
2,β
3,β
4也线性无关.
设存在一组数k
1,k
2,k
3,k
4,使k
1β
1+k
2β
2+k
3β
3+k
4β
4=0,
则k
1α
1+k
2(α
1+α
2)+k
3(α
1+α
2+α
3)+k
4(α
1+α
2+α
3+α
4)=0,
即(k
1+k
2+k
3+k
4)α
1+(k
2+k
3+k
4)α
2+(k
3+k
4)α
3+k
4α
4=0,
又因为α
1,α
2,α
3,α
4线性无关,故
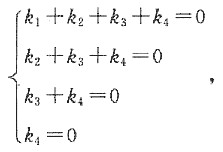
从而得,k
1=k
2=k
3=k
4=0,所以向量组β
1,β
2,β
3,β
4也线性无关.
[考点] 本题主要考查的知识点为向量组线性无关的判断.
 =5(t+2)=0,故t=-2.
=5(t+2)=0,故t=-2.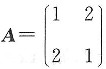 ,则在实数域上与A合同的矩阵为______
,则在实数域上与A合同的矩阵为______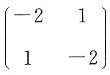
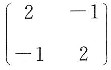
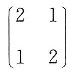
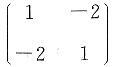
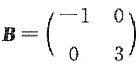 ,而选项中各个对称矩阵与对角矩阵B合同的只有选项D.
,而选项中各个对称矩阵与对角矩阵B合同的只有选项D.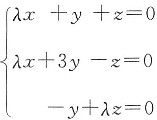 仅有零解,则______
仅有零解,则______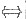
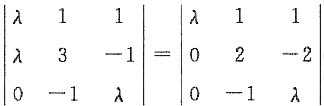 =2λ(λ-1)≠0,即λ≠0且λ≠1.
=2λ(λ-1)≠0,即λ≠0且λ≠1.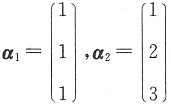 是三元线性方程组Ax=b(b≠0)的解,且r(A)=2,则Ax=b的通解为______.
是三元线性方程组Ax=b(b≠0)的解,且r(A)=2,则Ax=b的通解为______.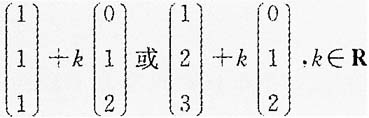
 ,则 A11+A12+A13+A14=______.
,则 A11+A12+A13+A14=______.
 ,则矩阵A的秩r(A)=______.
,则矩阵A的秩r(A)=______.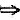 r(A)≥1,故r(A)=1.
r(A)≥1,故r(A)=1.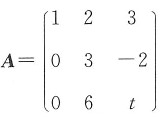 ,当t=______时,r(A)=2.
,当t=______时,r(A)=2.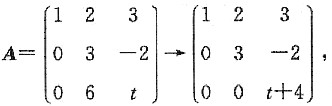
 ,则r(A)=______.
,则r(A)=______.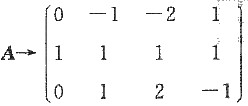
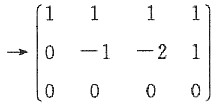 ,故r(A)=2.
,故r(A)=2. |ATA|=|AT||A|=|A|2=1
|ATA|=|AT||A|=|A|2=1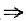 |A|=1或-1.
|A|=1或-1.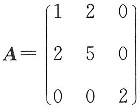 ,则A-1=______.
,则A-1=______.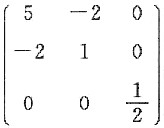
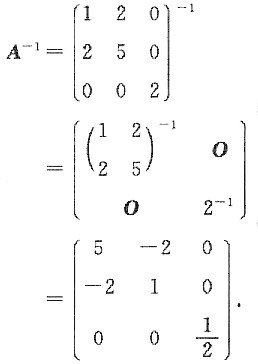
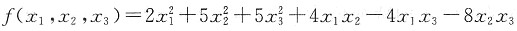 ,用正交变换化f(x1,x2,x3)为标准形,并求出其正交变换矩阵Q.
,用正交变换化f(x1,x2,x3)为标准形,并求出其正交变换矩阵Q. 4x1x2-4x1x3-8x2x3,
4x1x2-4x1x3-8x2x3,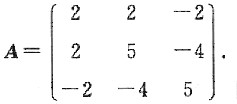
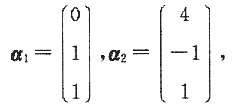

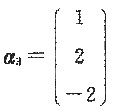 ,单位化得
,单位化得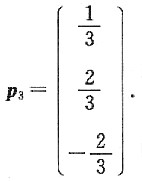
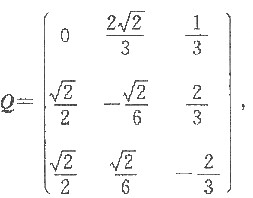
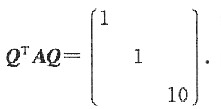
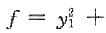
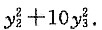
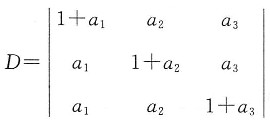
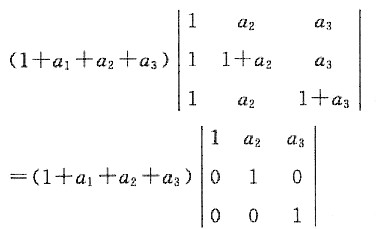
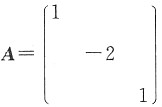 ,求B.
,求B.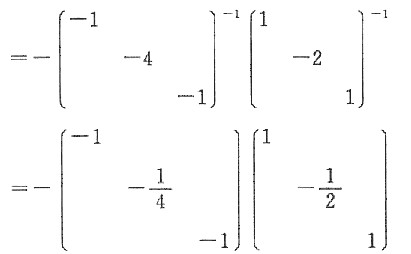

 ,求A21+A22+A23+A24.
,求A21+A22+A23+A24.
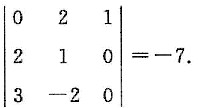
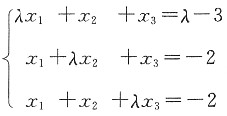 ,有唯一解,无解和有无穷多解?当方程组有无穷多解时求其通解.
,有唯一解,无解和有无穷多解?当方程组有无穷多解时求其通解.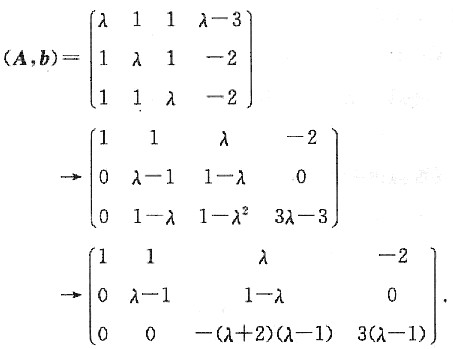

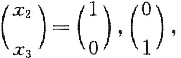
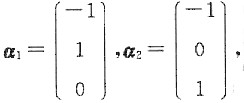
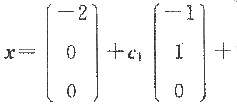
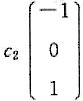 (c1,c2为任意常数).
(c1,c2为任意常数). 的秩和列向量组的极大无关组,并用其表示向量组中其余向量.
的秩和列向量组的极大无关组,并用其表示向量组中其余向量.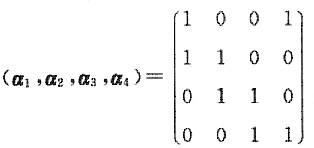

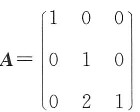 ,求A的特征值及其对应的特征向量.
,求A的特征值及其对应的特征向量.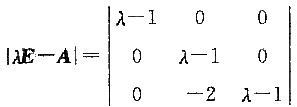
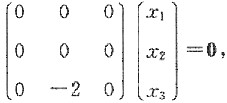

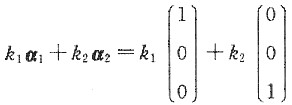 ,其中k1,k2是不全为零的任意常数.
,其中k1,k2是不全为零的任意常数.