二、填空题1.
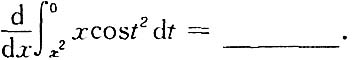
2.
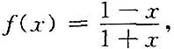
则f
(n)(x)=______.
3.
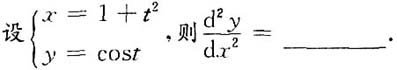
4. 设函数y=y(x)由方程e
x+y+cos(xy)=0确定,则

5. 已知f(-x)=-f(x)且f'(-x
0)=k,则f'(x
0)=______.
6. 设f(x)可导,则
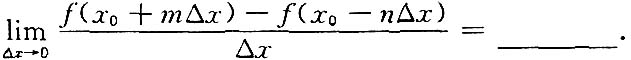
7. 设
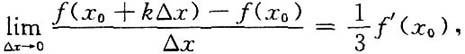
则k=______.
8.
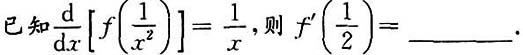
9. 设f为可导函数,y=sin{f[sinf(x)]},则

f'(x)cosf(x)f'[sinf(x)]·cos{f[sinf(x)]}.
10. 设函数y=f(x)由方程e
2x+y-cos(xy)=e-1所确定,则曲线y=f(x)在点(0,1)处的法线方程为______.
三、解答题设f'(x0)存在,求下列各极限.1.
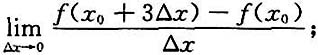
[解]
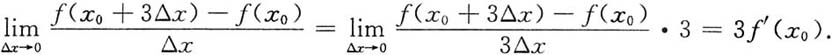
2.
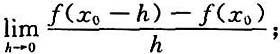
[解]
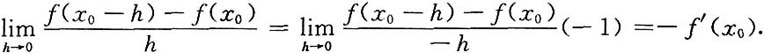
3.
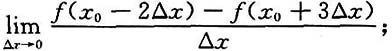
[解]
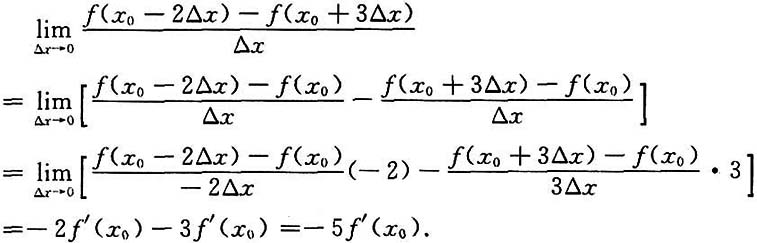
4.
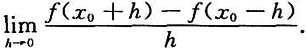
[解]
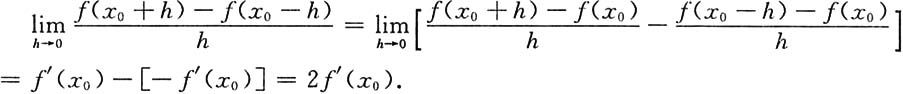
5. 设f(x)在x=1处连续,且
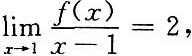
求f'(1).
[解]
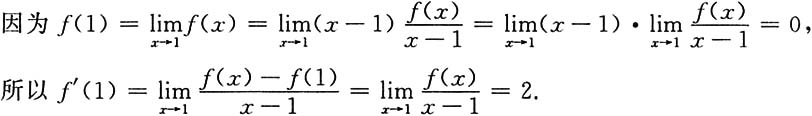
6. 设f(x)在(-∞,+∞)内有定义,对任意x,恒有f(x+1)=2f(x).当0≤x≤1时,f(x)=x(1-x
2),试判断在x=0处,f'(x)是否存在.
[解]当-1≤x<0时,0≤x+1<1,于是
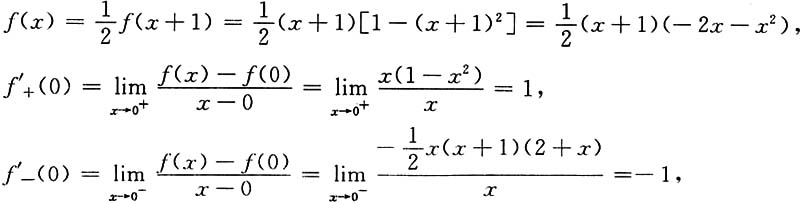
因为f'
+(0)≠f'
-(0),所以f(x)在x=0处不可导.
7. 求抛物线
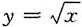
在点M(1,1)处的曲率圆方程.
[解]由题设可知:
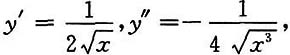
则
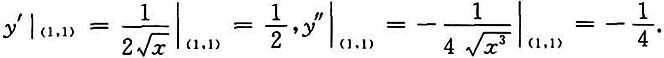
设
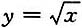
在点(1,1)处的曲率圆方程为
(x-α)
2+(y-β)
2=R
2,
其中
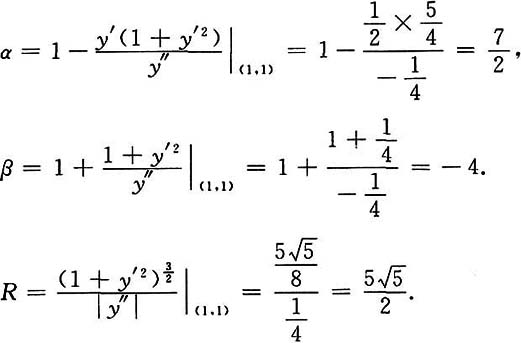
故
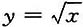
在点(1,1)处的曲率圆方程为
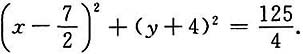
8.
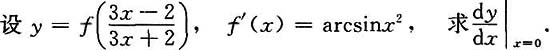
[解]
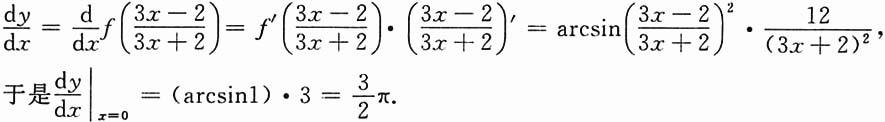
9. y=x[cos(lnx)+sin(lnx)];
[解]
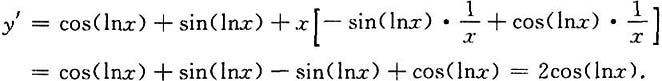
10. y=f
n[φ
n(sinx
n)];
[解]y'=nfn-1[φn(sinxn)]·f'[φn(sinxn)]·nφn-1(sinxn)·φ'(sinxn)·cosxn·nxn-1
=n3·xn-1cosxn·fn-1[φn(sinxn)]·φn-1(sinxn)·f'[φn(sinxn)]·φ'(sinxn).
11. y=x
aa+a
xa+a
ax(a>0).
[解]y'=aaxaa-1+axa·lna·axa-1+aaxlna·axlna
=aaxaa-1+alnaxa-1axa+ln2a·axaax.
12. 设
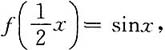
求f'[f(x)],{f[f(x)]}',{f[f(x)]}".
[解]令
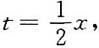
则f(t)=sin2t,f'(t)=2cos2t,f"(t)=-4sin2t.
于是f'[f(x)]=2cos2[f(x)]=2cos(2sin2x);
{f[f(x)]}'=f'[f(x)]·f'(x)=2cos(2sin2x)·2cos2x
=4cos(2sin2x)·cos2x;
{f[f(x)]}"={f'[f(x)]·f'(x)}'=f"[f(x)][f'(x)]
2+f'[f(x)]f"(x)
=-4sin(2sin2x)·(2cos2x)
2+2cos(2sin2x)·(-4sin2x)
=-16sin(2sin2x)cos
22x-8cos(2sin2x)(sin2x).
13. 作变换u=tany,x=e
t,试将方程

化为u关于t的方程.
[解]由于y=arctanu,t=lnx,故有
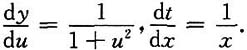
又
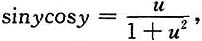
于是
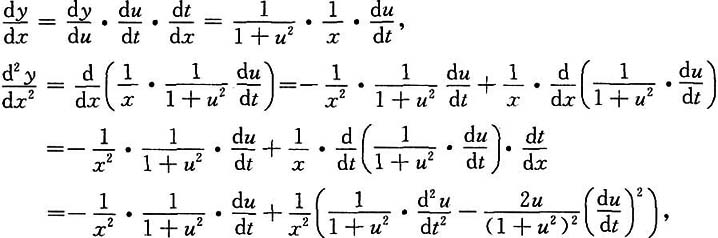
代入原方程得
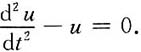
15. 设
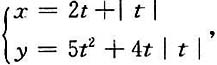
求当t=0时的导数

16. 设
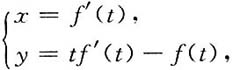
其中f(t)的三阶导数存在,且f"(t)≠0,
求
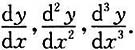
[解]
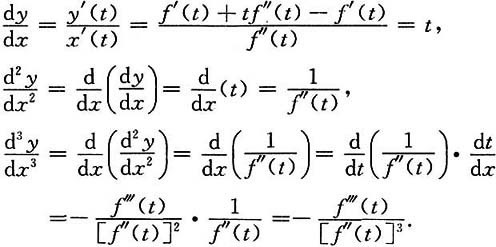
17. 设方程xy
2+e
y=cos(x+y
2),求y'.
[解法一]y
2+2xyy'+e
yy'=-sin(x+y
2)·(1+2yy'),
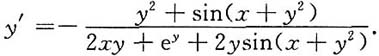
[解法二]令F(x,y)=xy
2+e
y-cos(x+y
2).
因为F'
x=y
2+sin(x+y
2),F'
y=2xy+e
y+2ysin(x+y
2),
所以
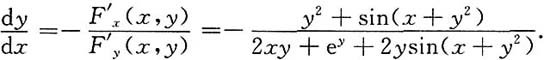
[解法三]d(xy
2+e
y)=d[cos(x+y
2)],
y
2dx+2xydy+e
ydy=-sin(x+y
2)(dx+2ydy),
[2xy+e
y+2ysin(x+y
2)]dy=-[y
2+sin(x+y
2)]dx,
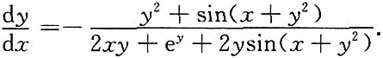
18. 设有方程
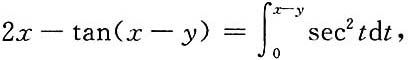
求
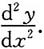
[解]方程两边对x求导,可得
2-sec
2(x-y)·(1-y')=sec
2(x-y)·(1-y')
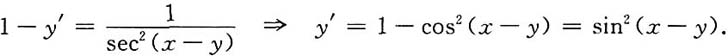
y"=2sin(x-y)cos(x-y)·(1-y')=2sin(x-y)cos(x-y)cos
2(x-y)
=2sin(x-y)cos
3(x-y).
19. 设由方程x
y=y
x确定y是x的函数,求
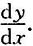
[解]e
ylnx=e
xlny,两边同时对x求导,得
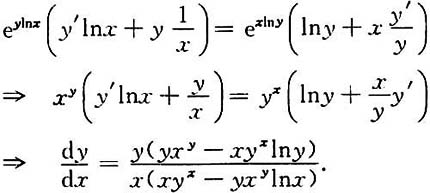
20. 设
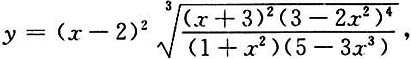
求y'.
[解]先将表达式写成分式指数幂的形式.

上式两边对x求导,得
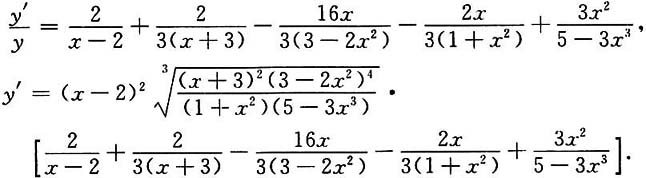
21. 设
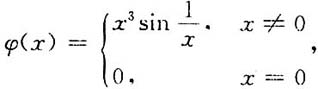
又函数f(x)可导,求F(x)=f[φ(x)]的导数.
[解]
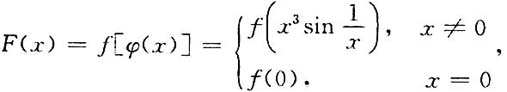
当x≠0时,
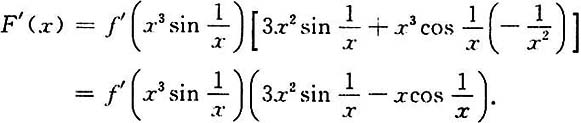
因为分界点x=0的两侧f(x)的表达式用同一形式表示,所以分界点处的导数只用一种形式求即可.
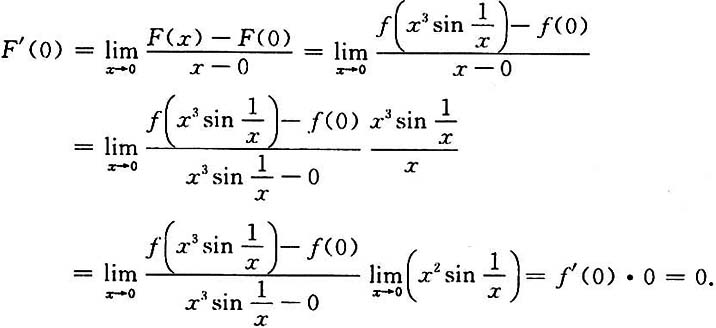
故
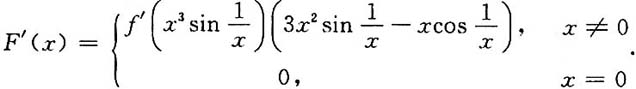
22. 设y=e
xcosx,求y
(n).
[解]
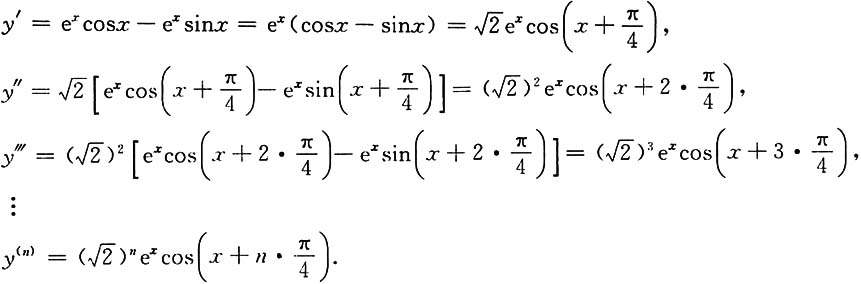
23. 设f(x)任意阶可导,且f'(x)=e
-f(x),f(0)=1.求f
(n)(0).
[解]f"(x)=-e
-f(x)f'(x)=-e
-2f(x),
f'''(x)=2e
-2f(x)f'(x)=2e
-3f(x),
f
(4)(x)=-3·2e
-3f(x)·f'(x)=-3·2e
-4f(x),

f
(n)(x)=(-1)
n-1(n-1)!e
-nf(x),
所以,f
(n)(0)=(-1)
n-1(n-1)!e
-nf(0)=(-1)
n-1(n-1)!e
-n.
24. 设
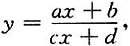
求y
(n).
[解]若c≠0,用多项式除法,可得
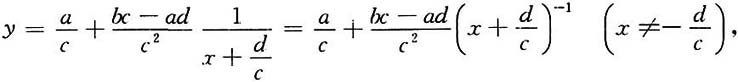
故
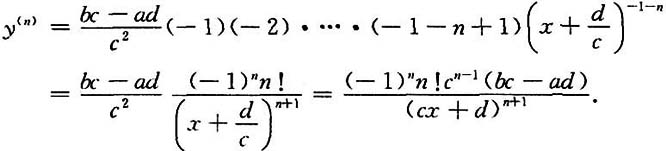
25. 设
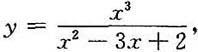
求y
(n)(n≥2).
[解]
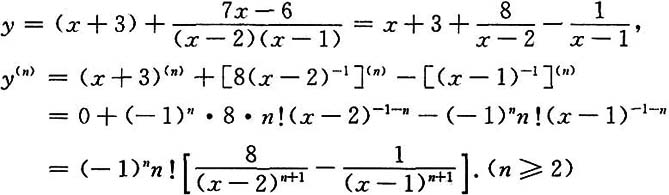
26. 设y=sinxsin2xsin3x,求y
(n).
[解]
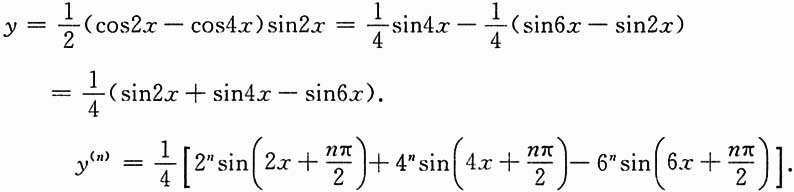
27. 设y=sin
6x+cos
6x,求y
(n).
[解]
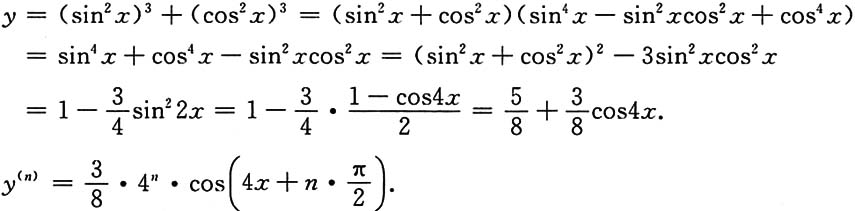
28. 设y=arcsinx,求y
(n)(0).
[解]因为
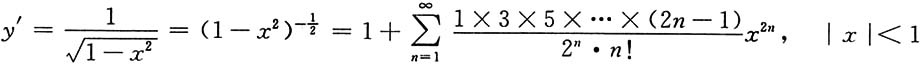
所以
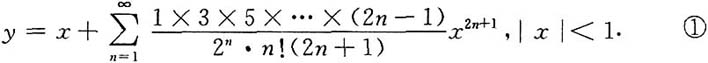
但由麦克劳林级数知
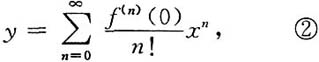
对比①与②中x
n的系数,得
y
(2k)(0)=f
(2k)(0)=0,y'(0)=1,
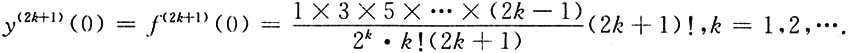
29. 设f(x)=arctanx,求f
(n)(0).
[解]因为
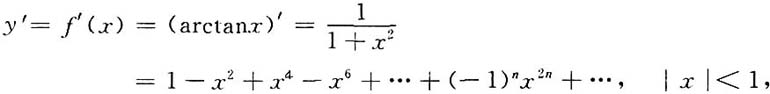
所以
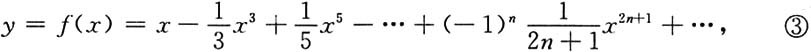
其中|x|<1,
又f(x)在x=0处的麦克劳林级数展开式为
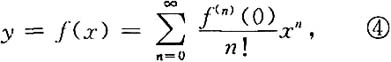
对比③,④中x
n的系数,得
f
(2k)(0)=0,
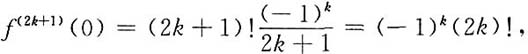
其中,k=0,1,2,….
30. 设
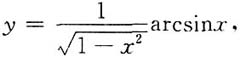
求y
(n)(0).
[解]
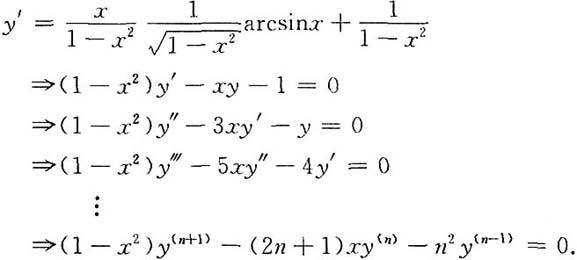
显然,当x=0时,y'=1,y"=0,y'''=4,…
故y
(2n)(0)=0,y
(2n+1)(0)=4
n(n!)
2.
31. 设f(x)=x
2ln(1+x),求f
(n)(0).
[解]
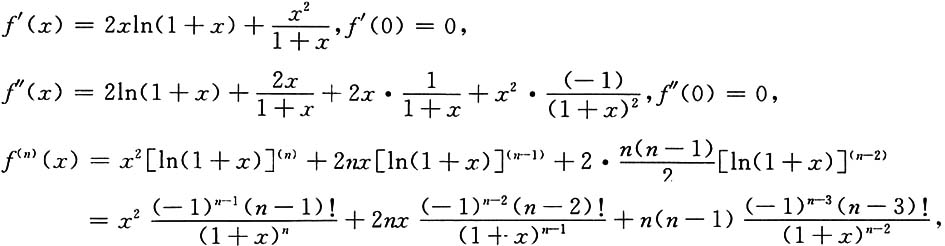
所以f
(n)(0)=(-1)
n-3(n-1)(n-3)!(n≥3).
32. 设f(x)在[a,b]上可导,f'
+(a)·f'
-(b)<0,证明:存在一点ξ∈(a,b),使f'(ξ)=0.
[证]不妨设f'
+(a)>0,f'
-(b)<0,于是
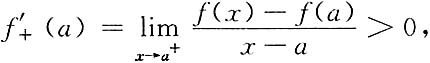
由极限保号性知,存在一个δ
1>0,当x∈(a,a+δ
1)时,恒有
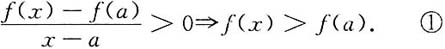
同理,
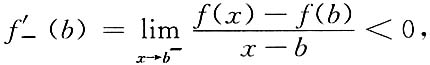
由极限保号性知,存在一个δ
2>0,当x∈(b-δ
2,b)时,恒有
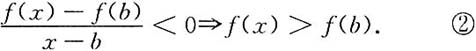
由f(x)在[a,b]上可导知,f(x)在[a,b]上连续,所以f(x)在[a,b]上必存在最大值,由①②知,最大值只能在(a,b)内取得.
令ξ∈(a,b),
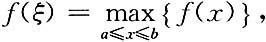
又f(x)在x=ξ处可导,故由费尔马定理知,f'(ξ)=0.
33. 已知f(x)是周期为5的连续函数,它在x=0的某邻域内满足关系式f(1+sinx)-3f(1-sinx)=8x+α(x),其中,α(x)是当x→0时比x高阶的无穷小,且f(x)在x=1处可导,求曲线y=f(x)在点(6,f(6))处的切线方程.
[解]由连续性,有
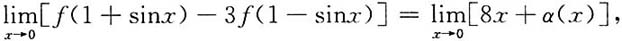
即f(1)-3f(1)=0,故f(1)=0.
因此,
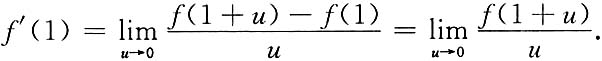
又
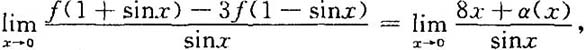
即
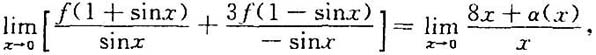
也即f'(1)+3f'(1)=8,故f'(1)=2.
由周期性
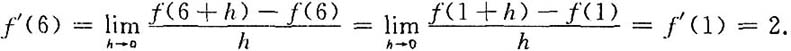
所以,要求的切线方程为y=2(x-6).
[解析] 曲线y=f(x)在点[6,f(6)]处的切线方程为y-f(6)=f'(6)(x-6).由周期性,f(6)=f(1),f'(6)=f'(1),故只需求f(1)与f'(1).又已知只给出f(x)在x=1处可导,所以利用导数定义求f'(1).
34. 设ρ=ρ(x)是抛物线
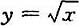
上任一点M(x,y)(x≥1)处的曲率半径,s=s(x)是该抛物线上介于点A(1,1)与M之间的弧长,求
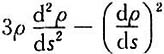
的值.
35. 设
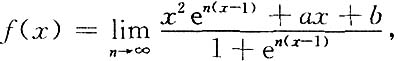
求f(x)并讨论f(x)的连续性与可导性.
[解]
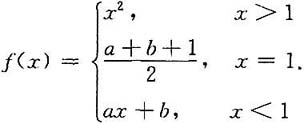
仅当f
-(1)=f
+(1)=f(1)时,f(x)在x=1处连续,
即
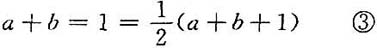
因此,当a+b=1时,f(x)在x=1处连续,显然f(x)在x≠1处连续,故当a+b=1时,f(x)在(-∞,+∞)上连续.
当f'
-(1)=f'
+(1)时,f(x)在x=1处可微.又注意到可微必连续,于是
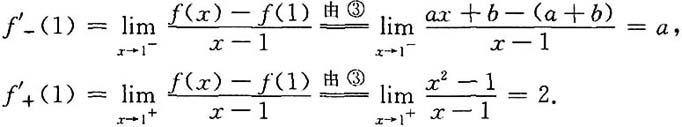
故仅当a=2,b=-1时,f'
-(1)=f'
+(1),即f(x)在x=1处可导,显然在x≠1处,f(x)也可导.
综上所述,当a=2,b=-1时,f(x)在(-∞,+∞)上可导.
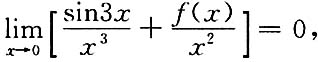
求:36. f(0),f'(0)和f"(0)的值;
[解]由题设知f(x)在点x=0的充分小邻域内有

(f(x)在点x=0的二阶泰勒公式),
所以,
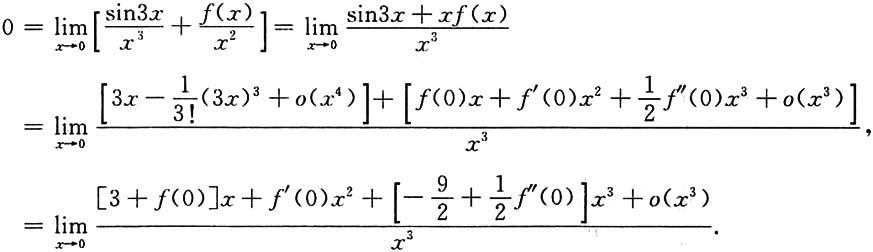
于是有
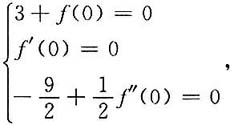
即f(0)=-3,f'(0)=0,f"(0)=9.
37.
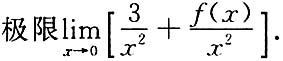
[解]由上小题知在点x=0的充分小邻域内有
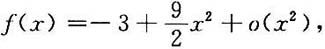
所以,
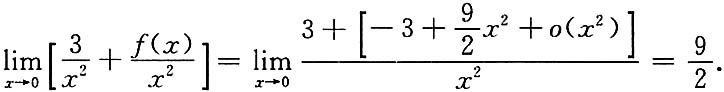
[解析] (1)由题设知,

(f(x)在点x=0的二阶泰勒公式).于是可由
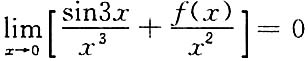
计算f(0),f'(0)和f"(0)的值.
(2)由上述f(x)的泰勒公式计算所给的极限.
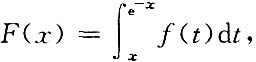 则F'(x)等于
则F'(x)等于 等于
等于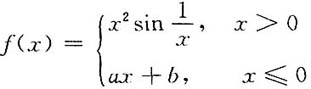 在x=0处可导,则
在x=0处可导,则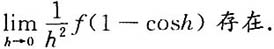
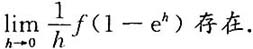
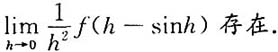
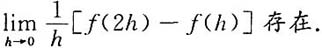
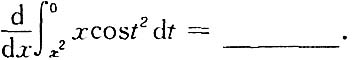
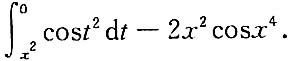
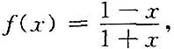 则f(n)(x)=______.
则f(n)(x)=______.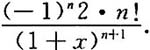
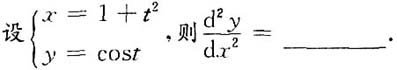
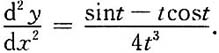

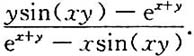
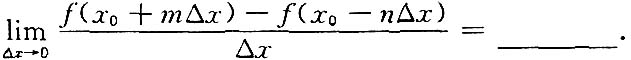
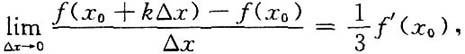 则k=______.
则k=______.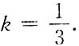
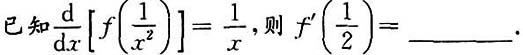


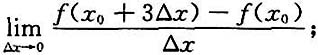
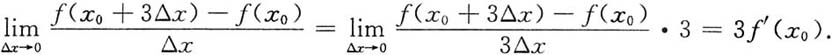
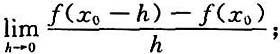
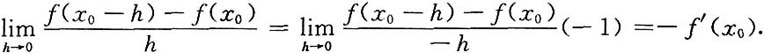
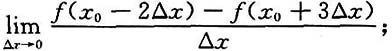
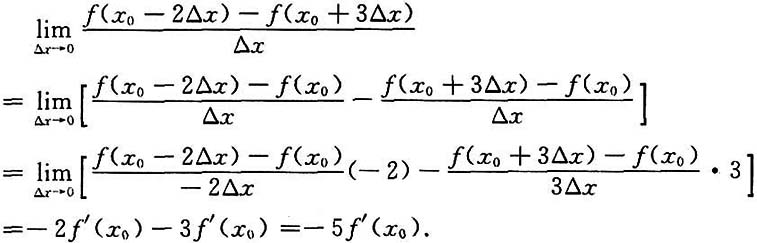
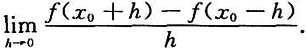
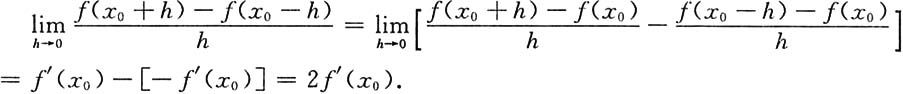
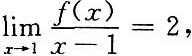 求f'(1).
求f'(1).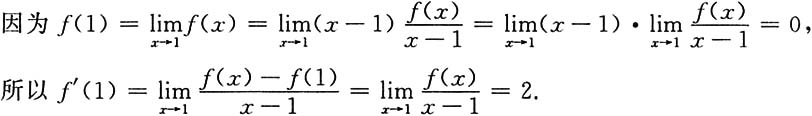
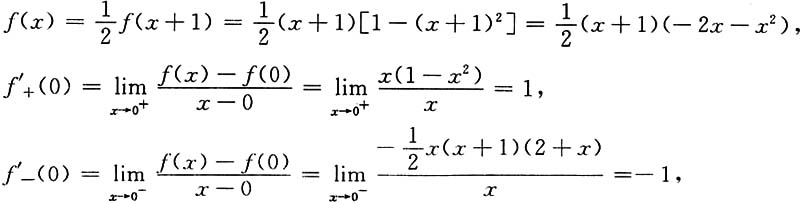
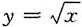 在点M(1,1)处的曲率圆方程.
在点M(1,1)处的曲率圆方程.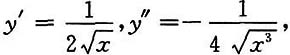
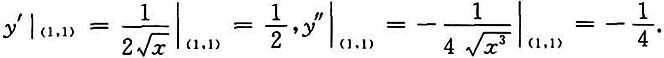
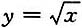 在点(1,1)处的曲率圆方程为
在点(1,1)处的曲率圆方程为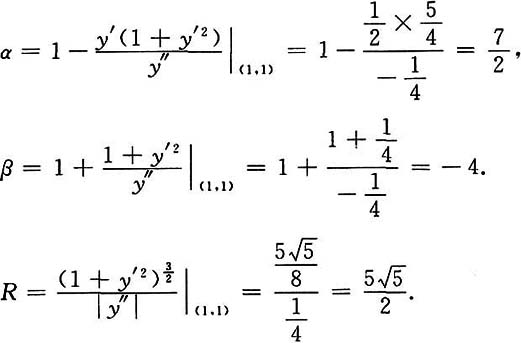
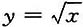 在点(1,1)处的曲率圆方程为
在点(1,1)处的曲率圆方程为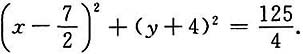
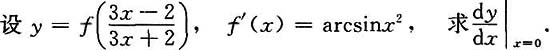
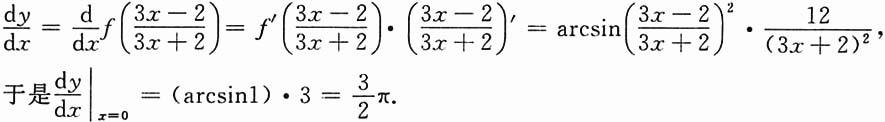
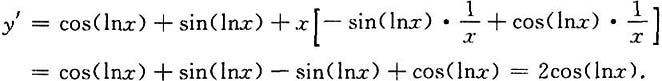
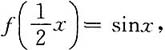 求f'[f(x)],{f[f(x)]}',{f[f(x)]}".
求f'[f(x)],{f[f(x)]}',{f[f(x)]}".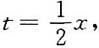 则f(t)=sin2t,f'(t)=2cos2t,f"(t)=-4sin2t.
则f(t)=sin2t,f'(t)=2cos2t,f"(t)=-4sin2t.
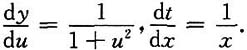 又
又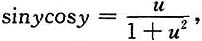
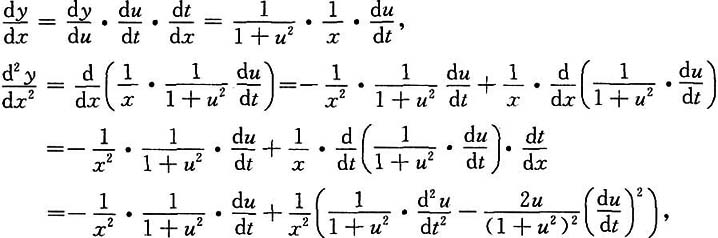
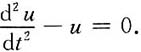
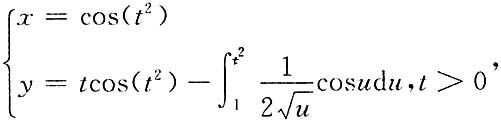 求
求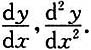
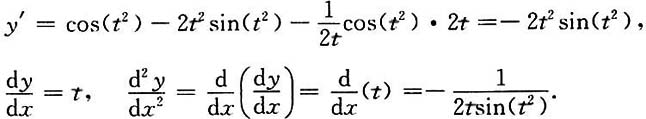
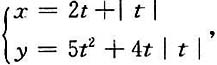 求当t=0时的导数
求当t=0时的导数
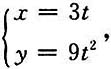 当t<0时,
当t<0时,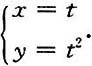
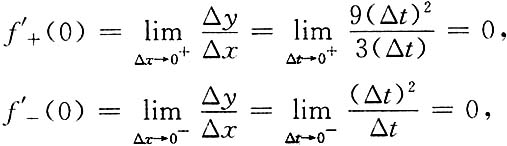
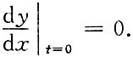
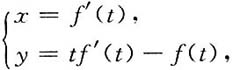 其中f(t)的三阶导数存在,且f"(t)≠0,
其中f(t)的三阶导数存在,且f"(t)≠0,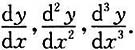
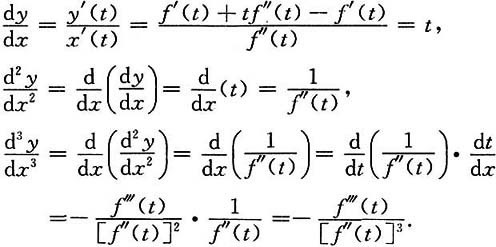
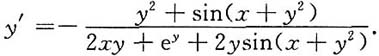
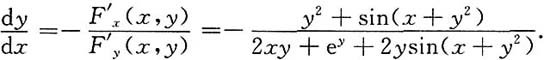
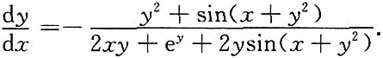
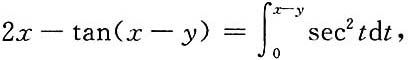 求
求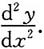
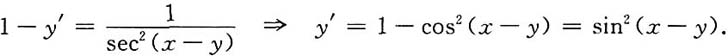
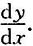
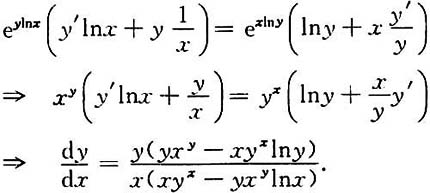
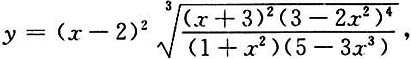 求y'.
求y'.
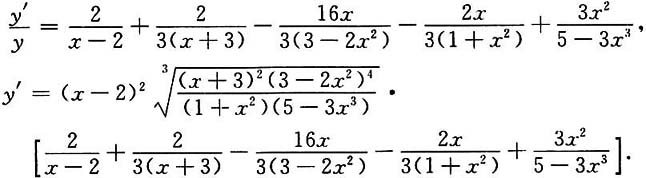
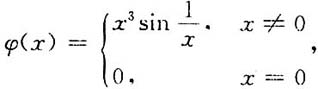 又函数f(x)可导,求F(x)=f[φ(x)]的导数.
又函数f(x)可导,求F(x)=f[φ(x)]的导数.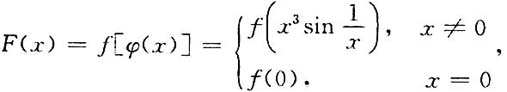
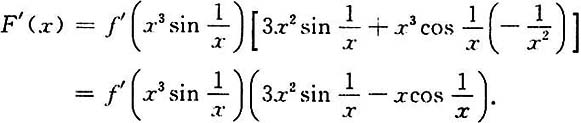
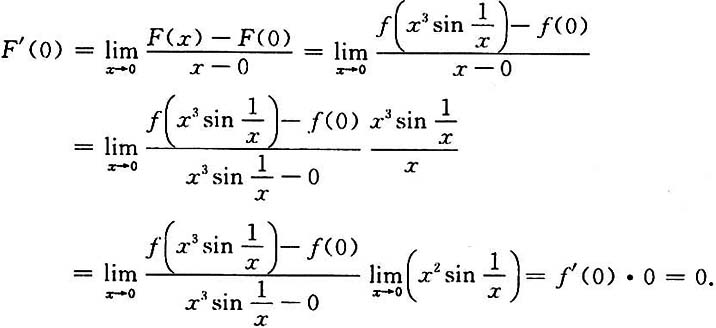
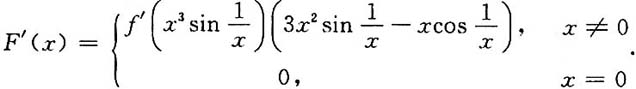
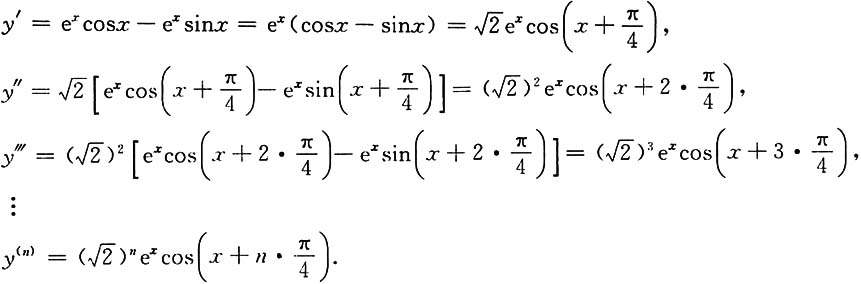

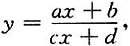 求y(n).
求y(n).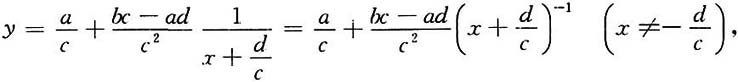
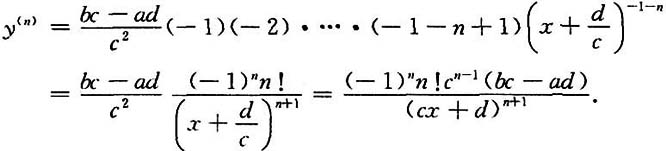
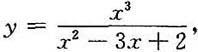 求y(n)(n≥2).
求y(n)(n≥2).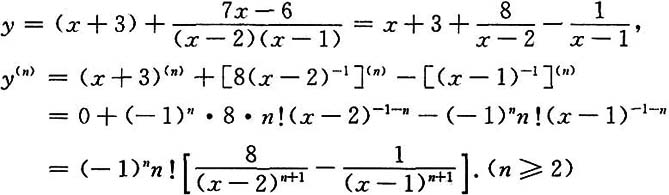
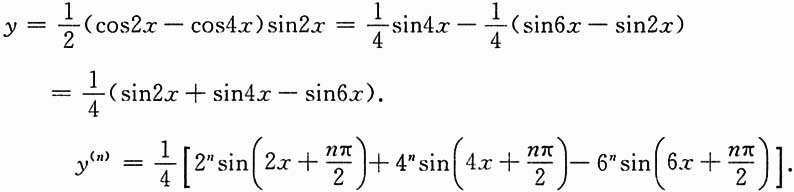
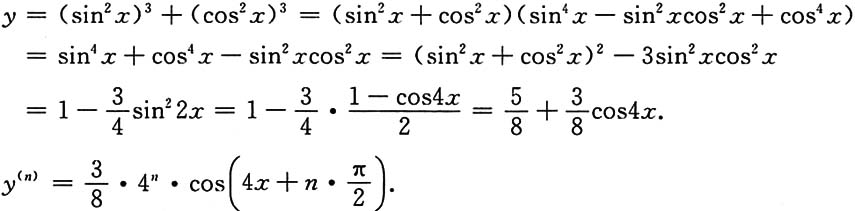
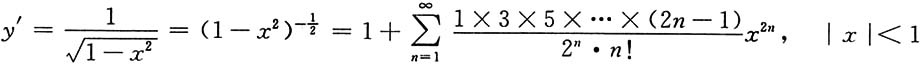
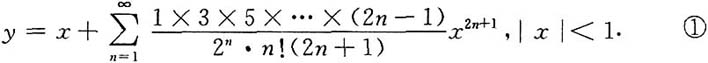
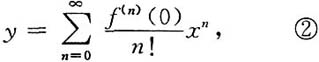
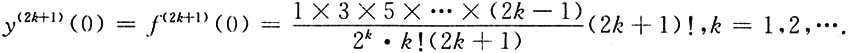
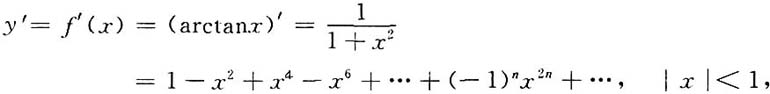
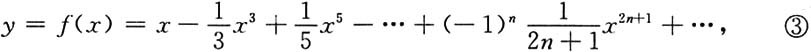
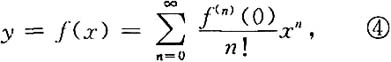
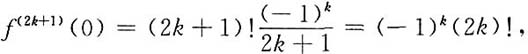 其中,k=0,1,2,….
其中,k=0,1,2,….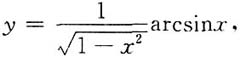 求y(n)(0).
求y(n)(0).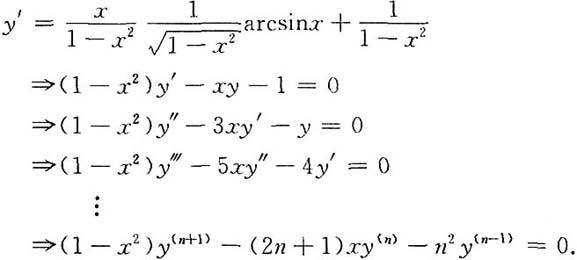
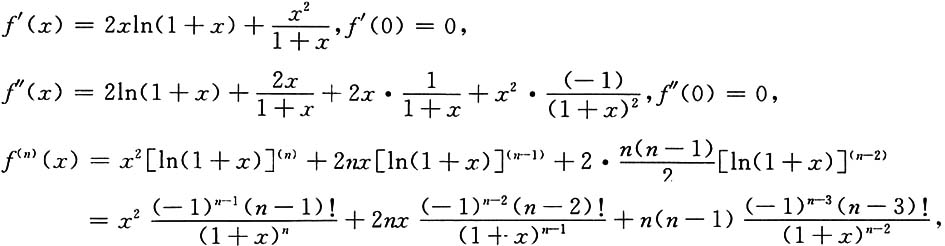
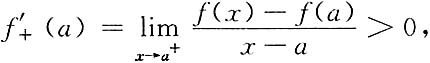
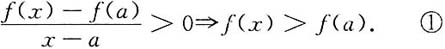
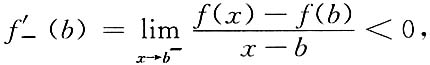
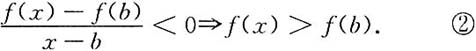
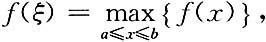 又f(x)在x=ξ处可导,故由费尔马定理知,f'(ξ)=0.
又f(x)在x=ξ处可导,故由费尔马定理知,f'(ξ)=0.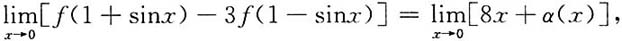
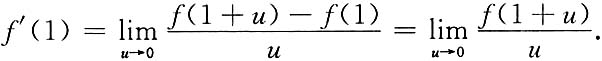 又
又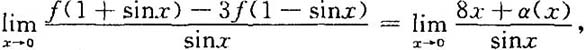
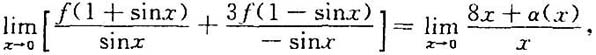
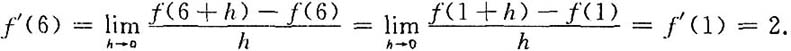
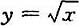 上任一点M(x,y)(x≥1)处的曲率半径,s=s(x)是该抛物线上介于点A(1,1)与M之间的弧长,求
上任一点M(x,y)(x≥1)处的曲率半径,s=s(x)是该抛物线上介于点A(1,1)与M之间的弧长,求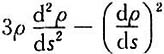 的值.
的值.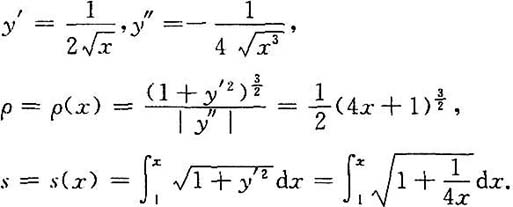
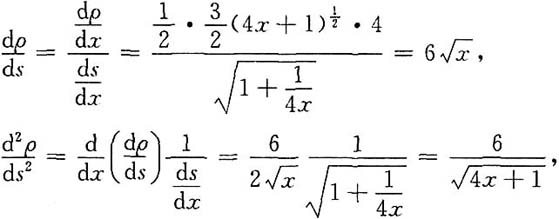
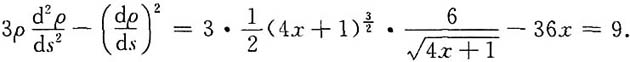
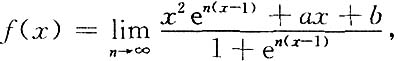 求f(x)并讨论f(x)的连续性与可导性.
求f(x)并讨论f(x)的连续性与可导性.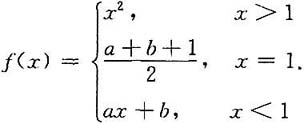
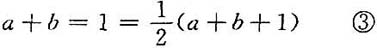
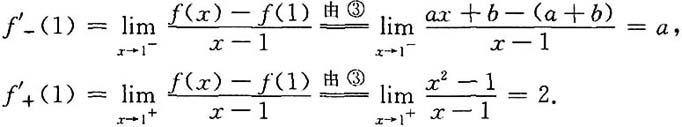
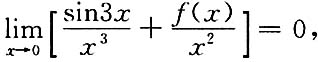
 (f(x)在点x=0的二阶泰勒公式),
(f(x)在点x=0的二阶泰勒公式),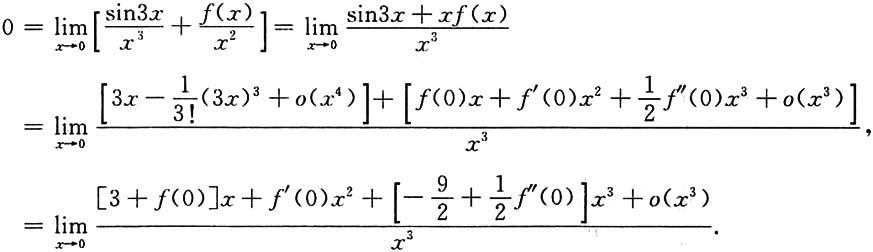
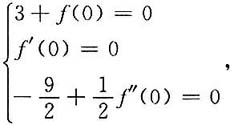
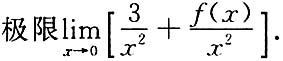
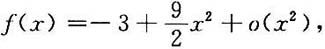
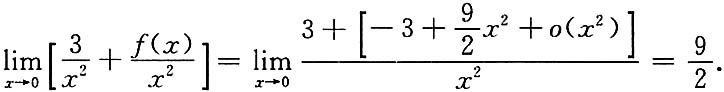
 (f(x)在点x=0的二阶泰勒公式).于是可由
(f(x)在点x=0的二阶泰勒公式).于是可由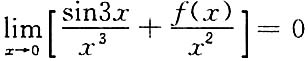 计算f(0),f'(0)和f"(0)的值.
计算f(0),f'(0)和f"(0)的值.