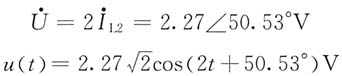二、填空题1. 当流过一个线圈中的电流发生变化时,在线圈本身所引起的电磁感应现象称为______现象;若本线圈电流的变化在相邻线圈中引起感应电压,则称为______现象。
2. 互感电压的正极性端与施感电流的入端构成______。
3. 两个耦合线圈,顺接串联时互感起______作用,反接串联时互感起______作用。
4. 两个互感线圈顺接串联时的等效电感为L
Z,反接串联时等效电感为L
F,则互感M=______。
5. 如题图所示电路,等效电感L
eq=______H。
6. 如题图所示电路,发生串联谐振的谐振角频率ω
0=______。
7. 电路如题图所示,已知
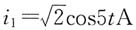
,i
2=0,
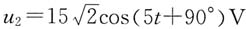
,则互感M=______。
8. 题图所示为一个耦合因数k=0.8的耦合电感的二端电路,其a、b两端的输入阻抗为______。
三、解答题1. 含耦合线圈的电路如下图所示,试列写耦合线圈的伏安关系式,并按顺时针方向列写线圈2回路的KVL方程。
解 此耦合电感电路中两施感电流i
1、i
2从异名端流入,磁通“削弱”,线圈自感电压与互感电压方向相反。
线圈1端电压u
1与i
1为关联参考方向,其上自感电压
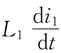
方向向下,而互感电压的正极性端与i
2的入端是同名端,因此互感电压
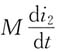
的方向向上。同理,线圈2自感电压
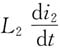
方向向下,互感电压
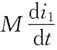
方向向上。综上,两线圈的伏安关系为

按照顺时针方向,线圈2回路的KVL方程为
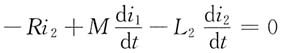
2. 下图(a)所示为含有耦合电感的一端口电路,角频率ω=2rad/s。(1)试求一端口电路的输入阻抗Z
ab;(2)判断一端口电路的性质;(3)画出串联等效电路。
解 对题图(a)中的耦合电感同名端为共同端的T形连接进行去耦等效,如题图(b)所示。
在角频率ω=2rad/s的电源作用下,其相量模型如题图(c)所示。
(1)输入阻抗
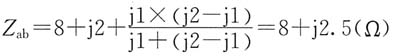
(2)输入阻抗的虚部大于0,该一端口电路呈感性。
(3)串联等效电路如图(d)所示。其中R
eq=8Ω,
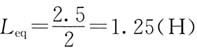
3. 正弦稳态电路图(a)所示,已知
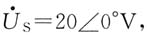
R
1=R
2=10Ω,ωL
1=10Ω,ωL
2=20Ω,ωM=12Ω,
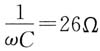
。(1)求两线圈的耦合因数k;(2)求开关S断开时的电流

和电压
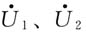
;(3)求开关S闭合时的电流

。
(1)耦合因数
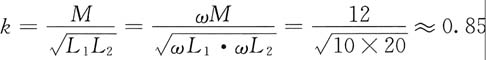
(2)开关S打开,两耦合线圈为反接串联。
解法一:根据耦合情况直接列方程
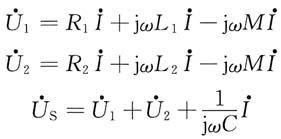
代入数据,方程组为
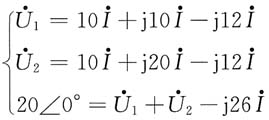
解得
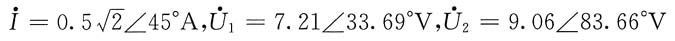
解法二:去耦等效电路如图(b)所示。两线圈的等效阻抗和电路的输入阻抗分别为
Z
1=R
1+jω(L
1-M)=10-j2(Ω)
Z
2=R
2+jω(L
2-M)=10+j8(Ω)
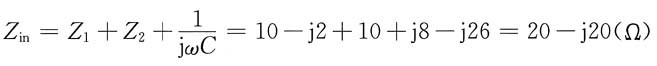
则
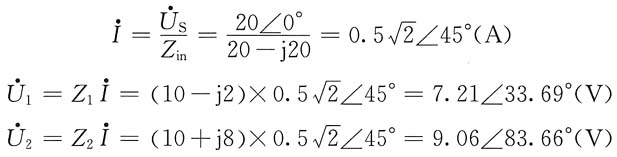
(3)开关S闭合。
解法一:设流过线圈2的电流为
,方向如图(c)所示。列方程

代入数据,方程组为
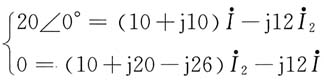
解得
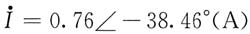
解法二:T形去耦等效电路如图(d)所示,列回路电流法方程
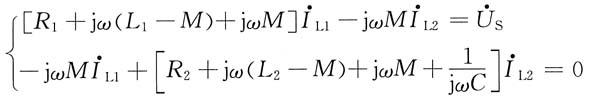
代入数据并整理,方程组为
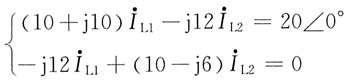
解得
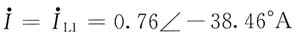
解法三:T形去耦等效电路如图(d)所示。电路输入阻抗
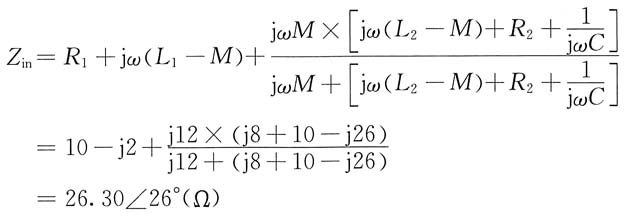
则
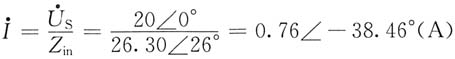
4. 正弦稳态电路如下图(a)所示,已知
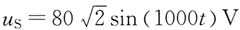
,L
2=0.12H,M=0.02H,C
1=C
2=50μF,R=80Ω。试求负载Z
L为何值时可获得最大功率,并求此最大功率。
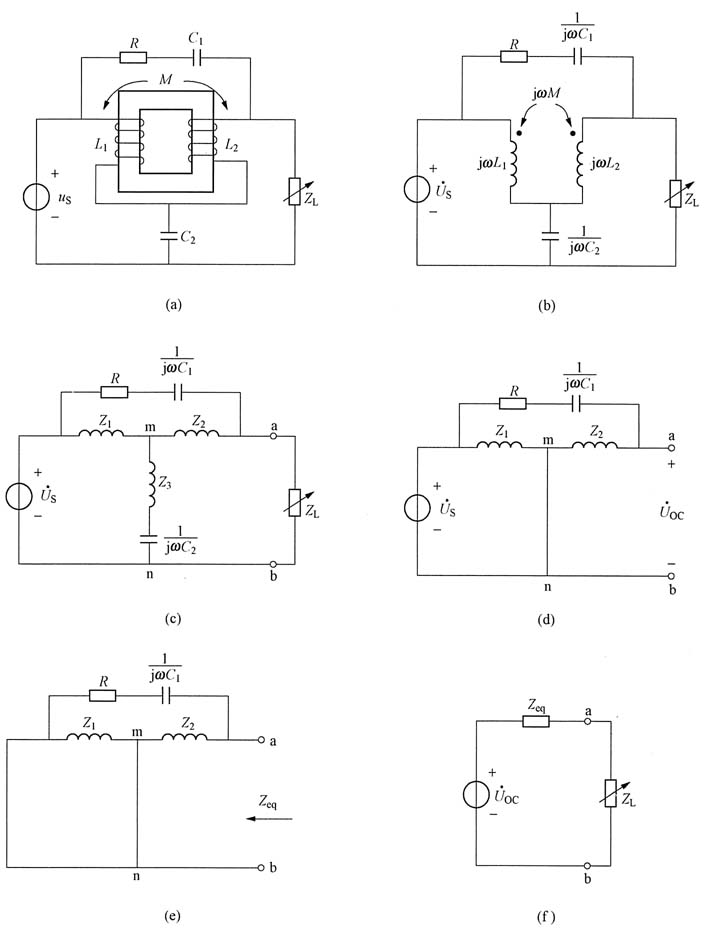
解 第一步:对图(a)根据耦合线圈绕向判断其同名端,画出电路相量模型如图(b)所示。其中:jωL
2=j120Ω,jωM=j20Ω,
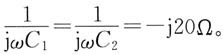
设
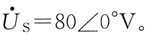
第二步:对图(b)中耦合电感T形连接去耦等效,电路如图(c)所示。其中:Z
1=jω(L
1-M)=j(1000L
1-20)Ω,Z
2=jω(L
2-M)=j100Ω,Z
3=jωM=j20Ω。
第三步:将图(c)中ab左右两部分断开,求ab以左含源网络的戴维南等效电路。
(1)求开路电压
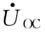
,电路如图(d)所示。
图(d)中
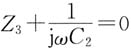
,所以Z
3与
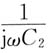
发生串联谐振,m、n两点可以用一条短路线代替。则

(2)求等效阻抗Z
eq,独立源

置零,电路如图(e)所示,其中Z
1被短路。
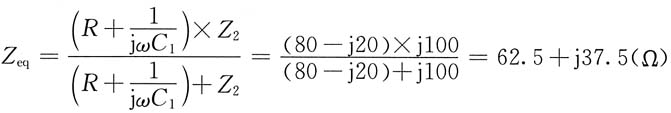
(3)画出ab以左含源网络的戴维南等效电路,加入Z
L得到电路如图(f)所示。
第四步:应用最大功率传输定理。
由共轭匹配条件可知,当
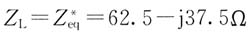
时,Z
L,可获得最大功率,且最大功率为
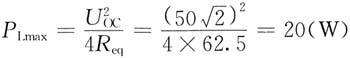
5. 正弦稳态电路如图(a)所示,已知
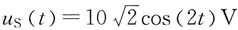
,求电压u(t)。
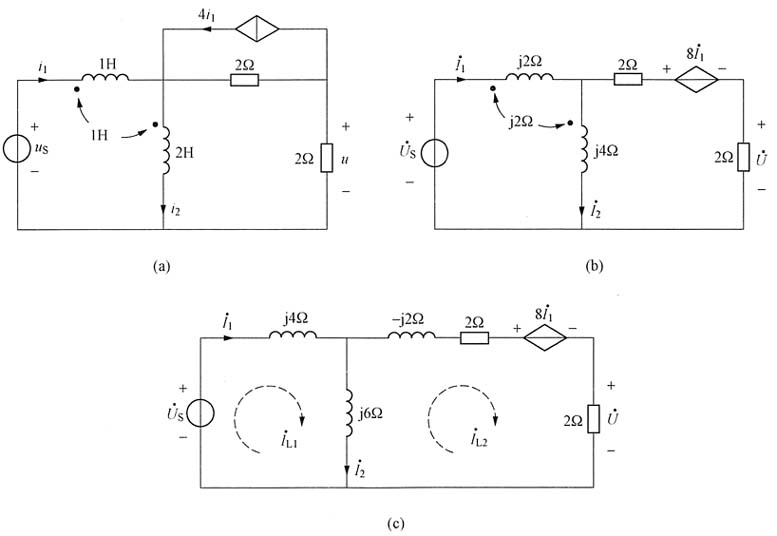
解
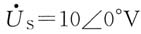
。电阻与受控电流源的并联可以等效为电阻与受控电压源的串联。画出图(a)所对应电路相量模型如图(b)所示。
解法一:直接列方程。列回路KVL方程
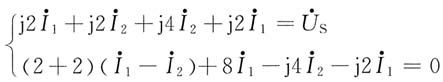
整理方程组,有
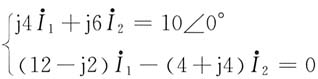
解得
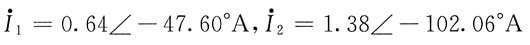
所以
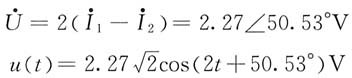
解法二:去耦等效法。对图(b)中耦合电感T形去耦,得到图(c)所示电路。应用回路电流法列方程
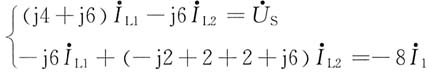
附加方程
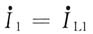
整理方程组,有
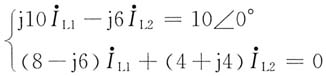
解得
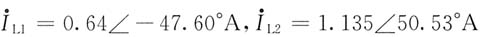
所以