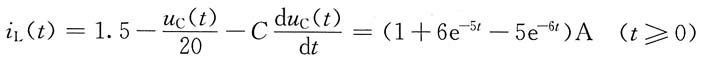一、选择题7. 题图所示电感元件的电压、电流关系的运算形式是______。
A．U
L(s)=sLI
L(s)-Li
L(0
-)
B．U
L(s)=sLI
L(s)+Li
L(0
-)
C．
D．
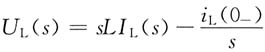
A B C D
二、填空题1. 已知某一阶电路电压响应的象原函数为
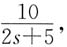
则该电路的时间常数为______。
2. 函数f(t)=te
-2t的拉普拉斯变换F(s)=______。
3. 象函数
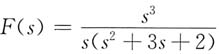
的拉普拉斯反变换f(t)=______。
4. 函数f(t)=t[ε(t)-ε(t-1)]的拉普拉斯变换F(s)=______。
5. 象函数
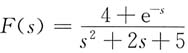
的拉普拉斯反变换f(t)=______。
2e-tsin(2t)ε(t)+0.5e-(t-1)sin2(t-1)ε(t-1)
6. 某无源二端网络的等效复频域导纳Y(s)=0.1+s，则该网络的等效复频域阻抗Z(s)=______。
7. 题图所示电感元件的电压、电流关系的运算形式是______。
8. 将题图(a)所示的运算电路化为图(b)所示的戴维南等效电路，则U
OC(s)=______，Z
eq(s)=______。
9. 题图所示电路的运算阻抗Z(s)是______。
10. 题图所示电路的运算导纳Y(s)是______。
三、解答题试求下列函数的象函数：1. f(t)=t+2+3δ(t)；
解
3. f(t)=2ε(t)-2ε(t-1)+3δ(t-3)。
4. 已知f(t)如图所示，求其拉普拉斯变换的象函数。
解 由图得函数的时域表达式为
f(t)=tε(t)-tε(t-1)+ε(t-1)-ε(t-2)
=tε(t)-(t-1)ε(t-1)-ε(t-2)
其象函数为
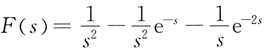
5. 求图(a)所示三角脉冲电流的象函数。
解 对电流i(t)求导，波形如图(b)所示，则
i'(t)=I
m[ε(t)-ε(t-1)]-I
m[ε(t-1)-ε(t-2)]
=I
mε(t)-2I
mε(t-1)+I
mε(t-2)
于是得到
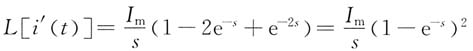
根据拉普拉斯的微分性质L[i'(t)]=sI(s)-i(0
-)，即得
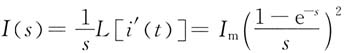
6.
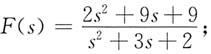
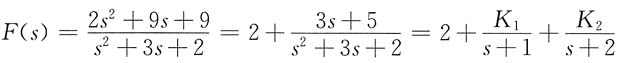
其中
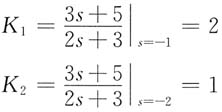
则 f(t)=2δ(t)+2e
-t+e
-2t
7.
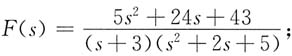
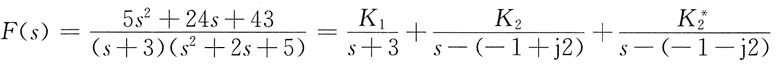
其中
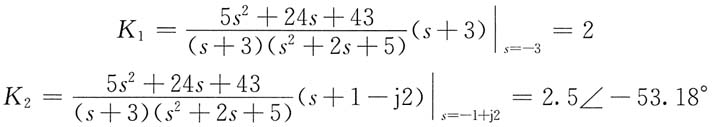
则
f(t)=2e
-3t+5e
-tcos(2t-53.18°)
8.
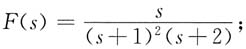
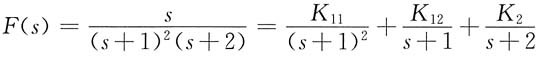
其中
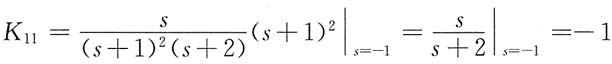
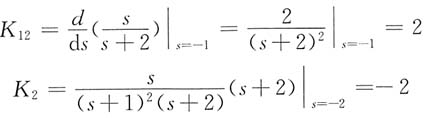
则
f(t)=-te
-t+2e
-t-2e
-2t
9.
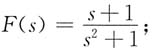
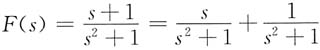
则
f(t)=cost+sint
10.
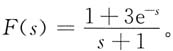
则
f(t)=e
-tε(t)+3e
-(t-1)ε(t-1)
11. 如图(a)所示电路原已处于稳态，开关S在t=0时闭合。试画出换路后电路的复频域模型(运算电路)。
解 由于开关S闭合前电路已达稳态，则
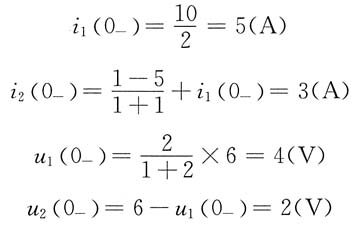
则换路后电路的复频域模型如图(b)所示。
12. 电路如图(a)所示，已知R
1=20Ω，R
2=40Ω，L=0.5H，C=50μF，U
S=40V。若原来电路已达稳态，t=0时闭合开关S，试画出换路后电路的复频域模型。
解 t=0-时刻电路处于直流稳态，则
iR1(0)=iL(0-)
(20+40)iL(0-)=40+20iL(0-)
解得
iL(0-)=1A
则
uC(0-)=40iL(0-)-20iL(0-)=40-20=20V
电路的复频域模型如图(b)所示。
13. 下图(a)所示电路原处于稳态，t=0时开关S闭合，试求换路后电流i
L(t)。
解 由于开关S闭合前电路已达稳态，电感电流i
L(0
-)=0，电容电压u
C(0
-)=1V。换路后电路的复频域模型如图(b)所示。
列写回路电流法方程
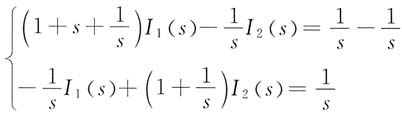
解得
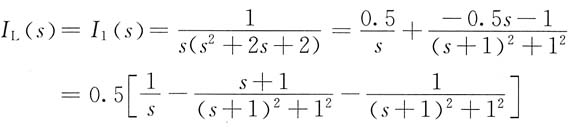
取拉普拉斯反变换得
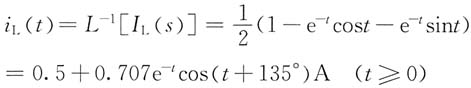
14. 图(a)所示电路，在开关S闭合前已处于稳态，t=0时开关S闭合，试用运算法求u
L(t)。
解 换路前电路处于直流稳态，电感短路，电容开路，所以
画出电路的复频域模型如图(b)所示。可得
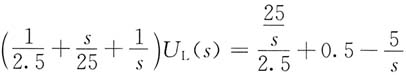
整理得
(s
2+10s+25)U
L(s)=12.5s+125
所以
取拉普拉斯反变换得
u
L(t)=(62.5t+12.5)e
-5t=12.5(5t+1)e
-5tV (t＞0)
15. 下图(a)所示电路，在开关S闭合前已处于稳态，t=0时开关S闭合，试用拉普拉斯变换法求u
C(t)。
解 换路前电路处于直流稳态所以
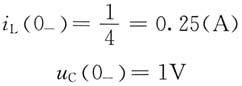
电路的复频域模型如图(b)所示。列写节点电压方程
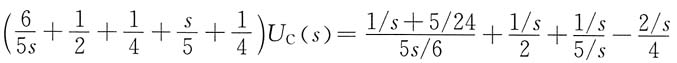
求得
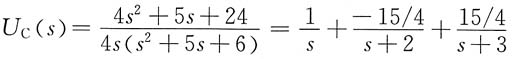
进行拉普拉斯反变换得
u
C(t)=1+3.75(-e
-2t+e
-3t)V t≥0
16. 如图(a)所示电路中，开关S在闭合前电路已经处于稳态，u
C1(0
-)=0，t=0时开关S闭合，求u
C2(t)。
解 由于开关S闭合前电路已达稳态，则
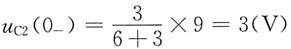
换路后的电路复频域电路模型如图(b)所示。列写节点电压方程
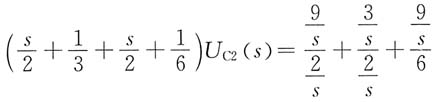
解得
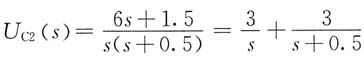
取拉普拉斯反变换得
u
C2(t)=L
-1[U
C2(s)]=(3+3e
-0.5t)V (t＞0)
17. 下图(a)所示电路，开关S在“1”处电路已达稳态，在t=0时开关S由1合向2，试求换路后电容电压u
C(t)和电感电流i
L(t)。
解 由于换路前电路已达稳态，则
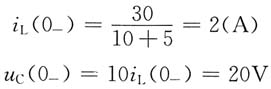
换路后的电路复频域模型如图(b)所示。
列写节点电压方程
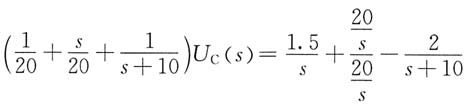
解得
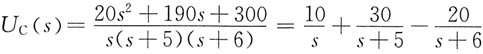
取拉普拉斯反变换得
u
C(t)=(10+30e
-5t-20e
-6t)V (t≥0)
i
L(t)=(1+6e
-5t-5e
-6t)A (t≥0)
另法求i
L(t)，根据换路后电路的时域模型，由KCL得
其所对应的原函数f(t)为______。
的拉普拉斯反变换式是______。
，则此元件是______。
深色：已答题 浅色：未答题