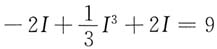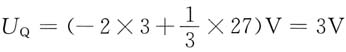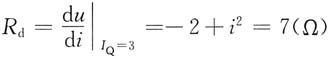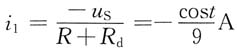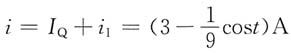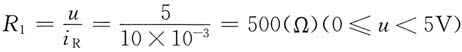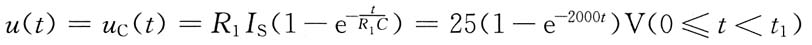二、填空题1. 叠加定理______用于分析非线性电路,特勒根定理______用于分析非线性电路。
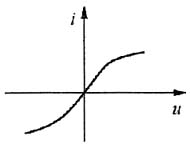
2. 电流控制型电阻是指电阻上的______是______的单调函数。
3. 电压控制型电阻是指电阻上的______是______的单调函数。
4. 电荷控制型电容是指电容上的______是______的单调函数。
5. 电压控制型电容是指电容上的______是______的单调函数。
6. 磁链控制型电感是指电感上的______是______的单调函数。
7. 电流控制型电感是指电感上的______是______的单调函数。
8. 当电阻上的电压是电流的______函数时,称为是流控的。
9. 当电感上的磁链是电流的______函数时,称为是流控的。
10. 当电容上的电荷是电压的______函数时,称为是压控的。
11. 设非线性电阻的伏安特性为u=f(i),则当i=I
0时的静态电阻R=______,而动态电阻R
d=______。
12. 设非线性电感的韦安特性为ψ=f(i),则当i=I
0时的静态电感L=______,而动态电感L
d=______。
13. 单向型电阻是指其特性与所加的端电压的______有关,例如______属于单向型电阻。
14. 在电阻伏安特性的下降段,其动态电阻为______零。(填“大于”或“小于”或“等于”)
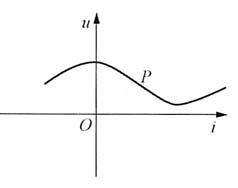
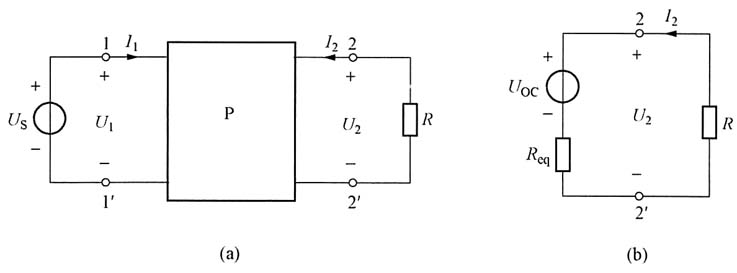
三、解答题1. 下图所示无源双口网络P的传输参数A=2.5,B=6Ω,C=0.5S,D=1.6。(1)求R为何值时,R吸收最大功率;(2)若U
S=9V,求R所吸收的最大功率P
max及此时U
S输出功率P。
解 由题目所给条件可得出无源双口网络P的传输方程为
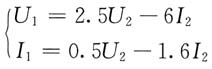
将U
1=U
S代入得

(1)由传输方程得
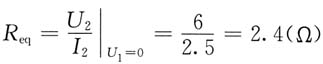
其中R
eq为2-2'端口以左部分的戴维南等效电阻,故知当R=R
eq=2.4Ω时,R吸收最大功率。
(2)当U
S=9V时,由传输参数第一个方程可得2-2'端口的开路电压
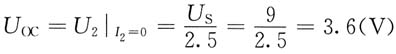
此时R吸收的最大功率为
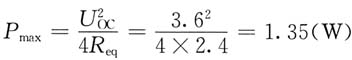
由题图(b)所示的等效电路可求出当R获得最大功率时,2-2'端口的电压、电流分别为
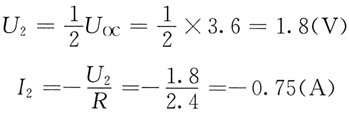
将U
2、I
2代入传输参数方程,得
I
1=0.5U
2-1.6I
2=0.5×1.8-1.6×(-0.75)=2.1(A)
所以,当R获得最大功率时,U
S输出的功率为
P=U
SI
1=9×2.1=18.9(W)
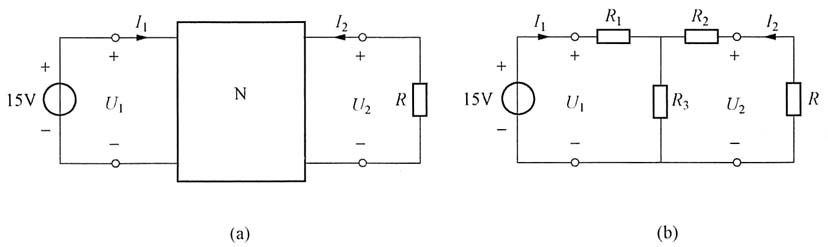
2. 下图(a)所示电阻性二端口网络,已知:R=∞时,U
2=7.5V;R=0时,I
1=3A,I
2=-1A。试求:(1)二端口网络的Z参数;(2)当R=2.5Ω时,I
1、I
2的值。
解 解法一:(1)将已知条件代入Z参数方程,得
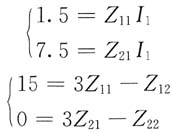
因为N为电阻性网络,所以有
Z
12=Z
21 解上述方程得
Z
11=6Ω,Z
12=Z
21=3Ω,Z
22=9Ω
(2)当R=2.5Ω时,有
U
1=6I
1+3I
2 U
2=3I
1+9I
2 U
1=15
U
2=-2.5I
2 解上述方程得
I
1=2.875A,I
2=-0.75A
解法二:设题图(b)中R
1、R
2、R
3组成的T形电路为图(a)中二端口N的等效电路,根据已知条件得

解上述方程得
R
1=R
3=3Ω,R
2=6Ω
(1)二端口网络的Z参数为
Z
11=R
1+R
3=6Ω,Z
12=Z
21=R
3=3Ω,Z
22=R
2+R
3=9Ω
(2)当R=2.5Ω时,由图(b)可求出

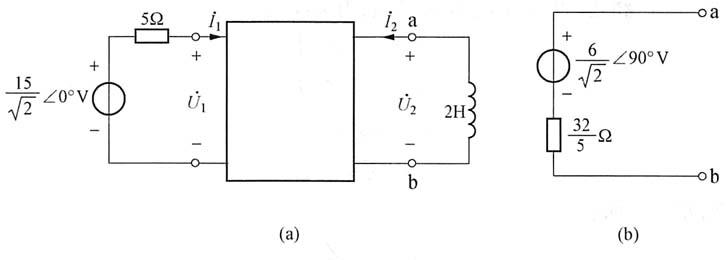
3. 下图(a)所示电路,在ω=2rad/s时,Z
11=10Ω,Z
12=Z
21=j6Ω,Z
22=4Ω,求a、b端的戴维南等效电路。
解 由题给条件得
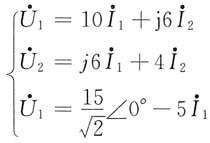
解法一:将上述方程中的第三式代入第一式,得
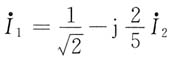
代入上述方程中的第二个式子,整理得
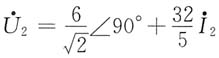
由此得出a、b端的戴维南等效电路[见题图(b)]。
解法二:令
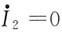
,可由上述方程求出此时的

,即为a、b端的开路电压
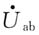
。将
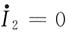
代入上述方程组可得

解方程得

再将输入端电压源置零,得方程如下:

解方程得

即
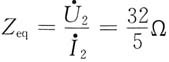
由求得的

及Z
eq,可得出a、b端戴维南等效电路,如题图(b)所示。
4. 下图所示电路中,二端口网络N不含独立源,其Y参数矩阵为

,t=0时闭合S,求换路后零状态响应i
L。
解 由已知条件可知,该二端口网络的Y参数方程为

当t<0时,开关未闭合,二端口网络N不含独立源,因此电感电流初始值为0,即
i
L(0
+)=i
L(0
-)=0
当t→∞时,电感元件在直流电源作用下可以视为短路,即U
2(∞)=0,此时U
1=1V。
i
L(∞)=I
2(∞)=5U
1=5A
从电感两端看进去的等效电阻

因此时间常数

将初始值、稳态值和时间常数代入三要素公式,可得电感电流
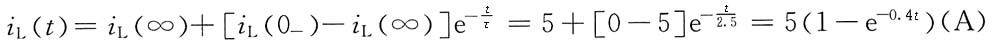
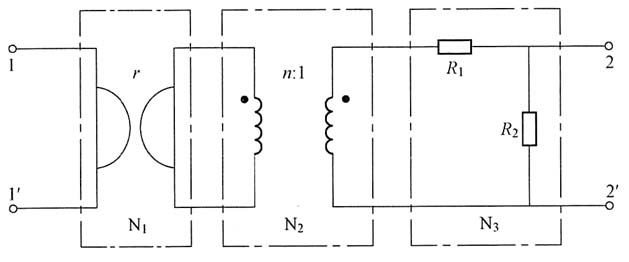
5. 如下图所示,已知r=10Ω,n=20,R
1=6Ω。求以1—1'和2—2'为端口的T参数矩阵。
解 将题图所示二端口网络分解为二端口网络N
1、N
2、N
3的级联,对每一个双口网络可容易地求出其传输参数矩阵。
网络N
1的传输参数矩阵为
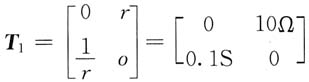
网络N
2的传输参数矩阵为

网络N
3的传输参数矩阵为

由级联时传输参数矩阵的关系可求得图示双口网络的传输参数矩阵为

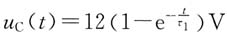 ;在图(b)所示电路中,当iS(t)=ε(t)A,C=400μF时,电容电压
;在图(b)所示电路中,当iS(t)=ε(t)A,C=400μF时,电容电压 。
。
6. 求此对称二端口的传输参数;
设对称二端口N的传输参数方程为

计算题图(a)所示电路的稳态解,可得
U
1=18V,I
2=0,U
2=12V
代入参数方程求得
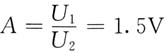
计算图(b)所示电路的稳态解,可得
I
1=1A,I
2=0,U
2=6V
代入参数方程求得
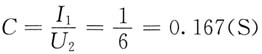
由AD-BC=1可得

故对称二端口的传输参数矩阵为

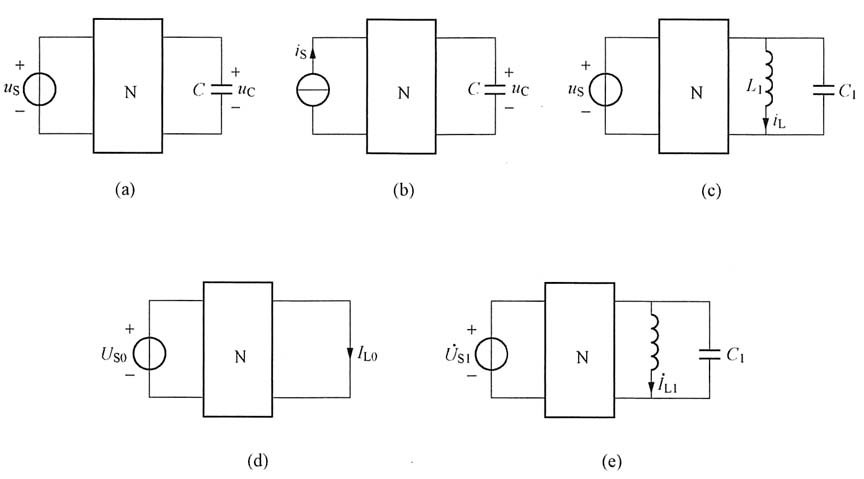
7. 若将此二端口网络等效为图(c)所示电路,其中
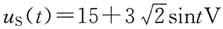
,L
1=2H,C
1=0.5F。求此电路的稳态响应i
L,并计算i
L的有效值。
题图(c)所示电路中电源为非正弦电源,用叠加法计算。
直流电压源U
S0=15V作用时,L
1短路,C
1开路,等效电路如图(d)所示。由参数方程及端口条件U
1=15V和U
2=0,可求得
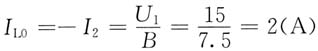
正弦电压源作用时,L
1、C
1发生并联谐振,

(开路),等效电路如图(e)所示。(采用相量法)
由参数方程及端口条件

可求得
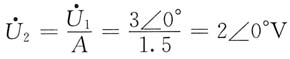
则

所以
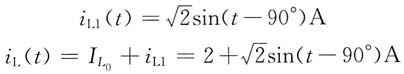
其有效值为
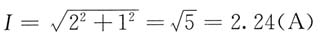
8. 已知图(a)所示电路中,二端口网络N的传输参数矩阵为
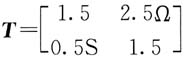
,t=0时闭合开关S。求零状态响应i
C(t)。
解 二端口网络N的传输参数方程为
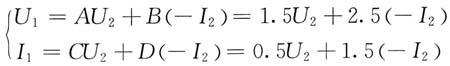
由其传输参数可以看出,该二端口为对称二端口(AD-BC=1,且A=D),将二端口网络用对称T形等效电路代替[见题图(b)],其传输参数为
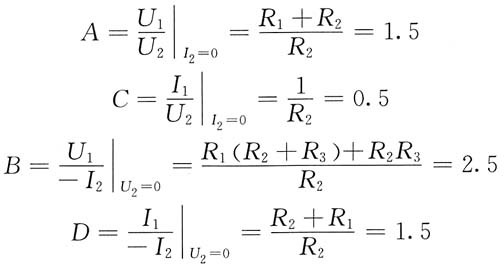
可解得
R
1=1Ω,R
2=2Ω
所以原电路可用图(c)所示电路等效。至此,本题变为一阶电路的零状态响应的求解问题,采用三要素法求电容电压。
初始值为
u
C(0
+)=u
C(0
-)=0
稳态值为
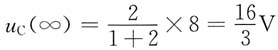
时间常数为

代入三要素公式,得
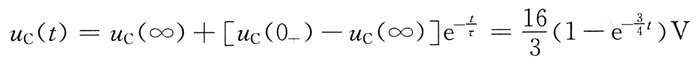
利用电容的VCR,得出电容电流的零状态响应为

9. 写出下图所示电路的节点电压方程。设电路中各非线性电阻的伏安特性为
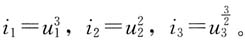
解 列节点①、②的KCL方程
i1+i
2=12
i
2+4=i
3 代入非线性电阻的伏安特性,可得
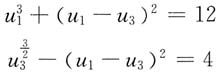
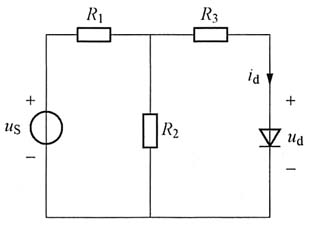
10. 下图所示电路,设二极管的伏安特性为i
d=10
-6(e
40ud-1)A,式中u
d为二极管的电压。已知R
1=R
2=0.5Ω,R
3=0.75Ω,u
S=2V。试用图解法求出静态工作点。
解 将二极管以左的线性电路用戴维南等效电路代替,如下图1所示,其中开路电压u
OC为
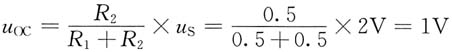
等效电阻R
eq为
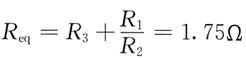
作二极管的伏安特性曲线与线性电路的伏安特性曲线,如图2所示。可求出其交点,即静态工作点:
u
d=0.34V,i
d=0.66A

图1
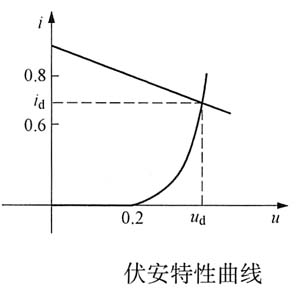
图2
11. 如下图所示非线性电阻电路中,非线性电阻的伏安特性为u=2i+i
3,现已知当u
S(t)=0时回路中的电流为1A。如果u
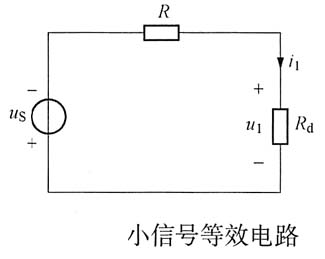
S(t)=cosωtV时,试用小信号分析法求回路中的电流i。
解 由题意可知,此电路的静态工作点在I
0=1A处,工作点处的动态电阻为
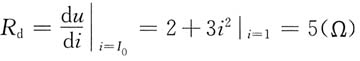
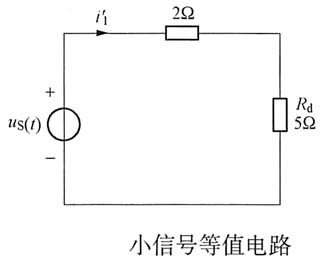
作出小信号等值电路(见下图),则
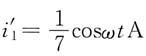
故总电流为
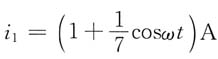
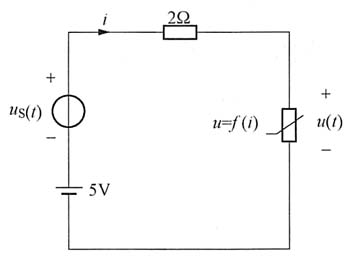
12. 如下图所示电路中R=2Ω,直流电压源U
S=9V,非线性电阻的伏安特性

若u
S(t)=cosωtV,试求电流i。
解 求电路的静态工作点。令u
S(t)=0V,则
U
S=RI+U
把非线性电阻的伏安特性

代入上式,可得
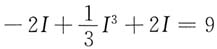
求解方程可得静态工作点
I
Q=3A,
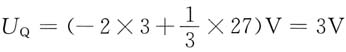
所以工作点处的动态电阻为
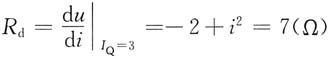
作小信号等效电路,如下图所示,则
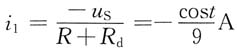
解得
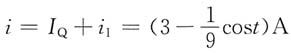
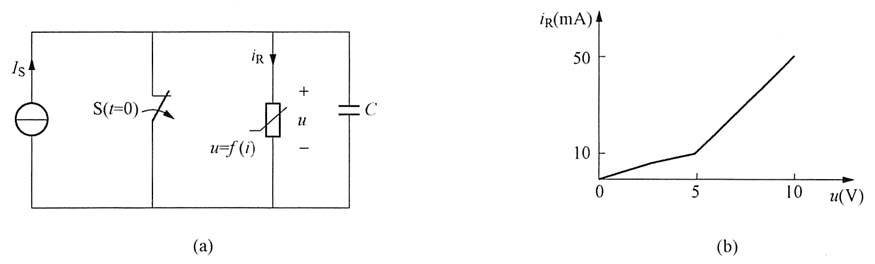
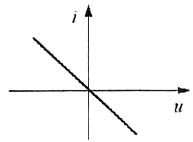
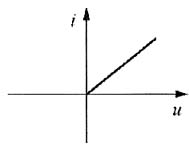
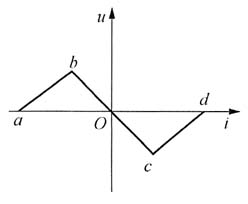
13. 在下图(a)所示电路中,开关S原为闭合,电路已达稳态。t=0时S打开,求u(t)。已知I
S=50mA,C=1μF,非线性电阻的伏安特性曲线如图(b)所示。
解 设电容电压充到u(t)=5V的时刻为t
1。
当0≤t<t
1时,由于u
C(0
+)=u
C(0
-)=0,S打开后,电容开始充电,u
C开始上升,非线性电阻上的电压u=u
C也开始上升。从图(b)可知,这段的非线性电阻可用一线性电阻R
1表示
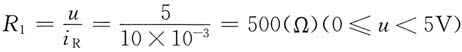
作出等效电路如图所示,则零输入响应为
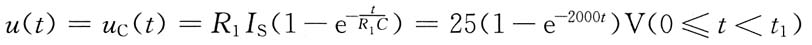
因u(t)=5V的时间为t
1,即
25(1-e
-2000t1)=5
可求得t
1=0.1116ms。
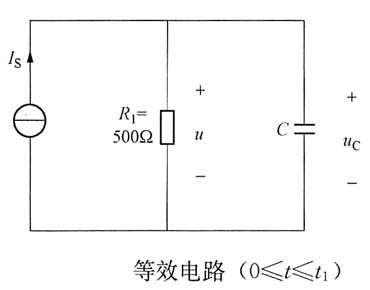
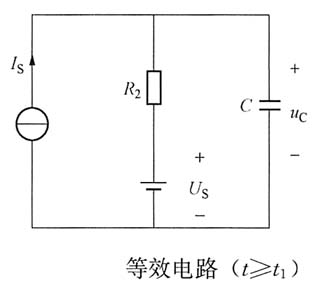
当t≥t
1时,这段非线性电阻的伏安特性可表示为
u=3.75+125i
R 作出等效电路,如下图所示,其中U
S=3.75V,R
2=125Ω。
用三要素法求解全响应
u
C(t
1+)=5V,u
C(∞)=R
2I
S+U
S=10V,τ
2=R
2C=125×10
-6S 所以全响应为
u(t)=u
C(t)=[10-5e
-8000(t-111.6×10
-6]V
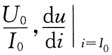
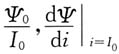
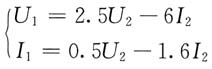

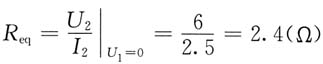
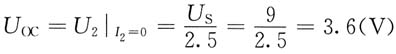
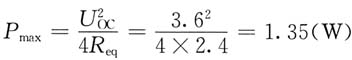
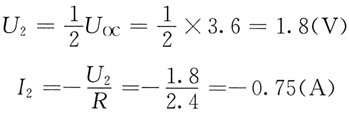
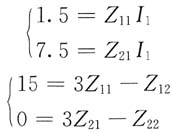


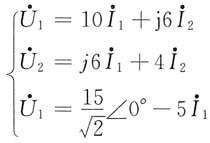
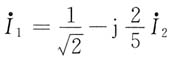
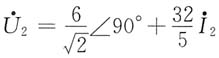
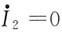 ,可由上述方程求出此时的
,可由上述方程求出此时的 ,即为a、b端的开路电压
,即为a、b端的开路电压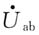 。将
。将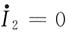 代入上述方程组可得
代入上述方程组可得



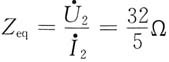
 及Zeq,可得出a、b端戴维南等效电路,如题图(b)所示。
及Zeq,可得出a、b端戴维南等效电路,如题图(b)所示。 ,t=0时闭合S,求换路后零状态响应iL。
,t=0时闭合S,求换路后零状态响应iL。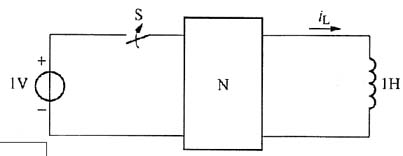



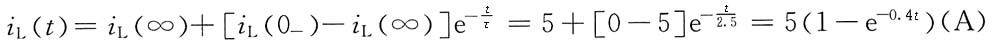
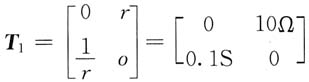



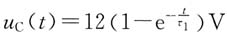 ;在图(b)所示电路中,当iS(t)=ε(t)A,C=400μF时,电容电压
;在图(b)所示电路中,当iS(t)=ε(t)A,C=400μF时,电容电压 。
。

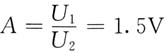
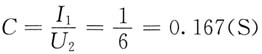


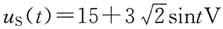 ,L1=2H,C1=0.5F。求此电路的稳态响应iL,并计算iL的有效值。
,L1=2H,C1=0.5F。求此电路的稳态响应iL,并计算iL的有效值。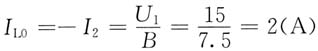
 (开路),等效电路如图(e)所示。(采用相量法)
(开路),等效电路如图(e)所示。(采用相量法)
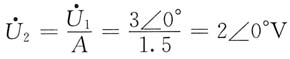

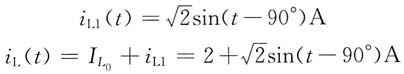
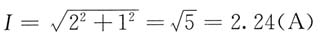
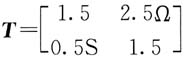 ,t=0时闭合开关S。求零状态响应iC(t)。
,t=0时闭合开关S。求零状态响应iC(t)。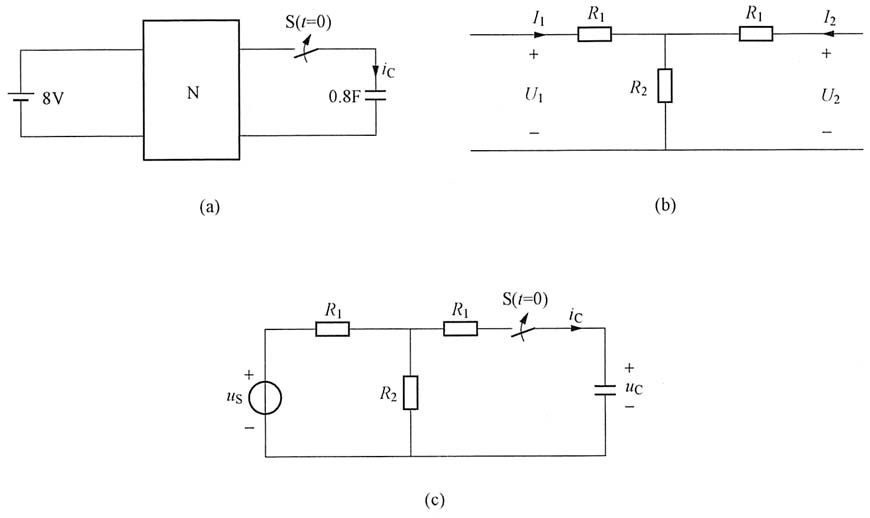
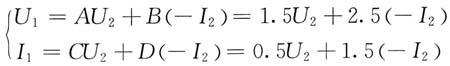
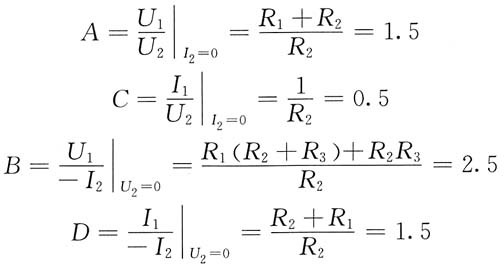
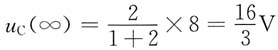

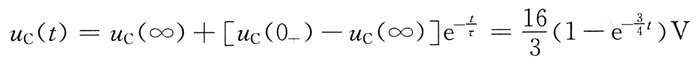

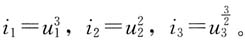

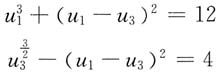
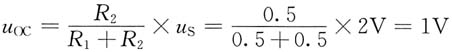
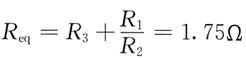


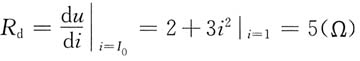
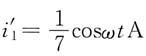
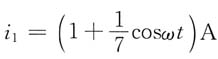
 若uS(t)=cosωtV,试求电流i。
若uS(t)=cosωtV,试求电流i。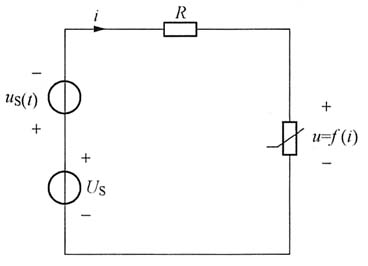
 代入上式,可得
代入上式,可得