一、单项选择题(在每小题的四个备选答案中选出一个正确答案)
5.

______
A.

B.

C.0
D.

A B C D
A
[解析]

故应选A.
6. 若

则f(x)=______
A.x+1 B.x+5
C.

D.

A B C D
C
[解析] 由题可知,
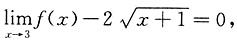
故f(3)=4,因此排除B、D选项,再将A、C代入原极限等式,可知C正确.
7. 设

要使f(x)在(-∞,+∞)上连续,则a=______
A.0
B.1
C.

D.3
A B C D
C
[解析]

根据连续的定义可知

10. 由参数方程

确定函数y(x)的二阶导数

______
A.

B.

C.

D.

A B C D
B
[解析] 因为
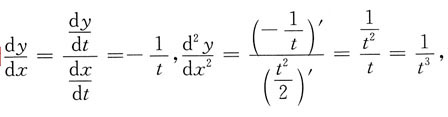
故应选B.
11. 设f
(2013)(x)=x
2+lnx,则f
(2016)(x)=______
A.

B.

C.

D.

A B C D
A
[解析]

故应选A.
13. 方程x
4-x-1=0至少有一个根的区间是______
A.

B.

C.(2,3)
D.(1,2)
A B C D
D
[解析] 令f(x)=x4-x-1,则f(1)=1-1-1=-1<0,f(2)=24-2-1=13>0,由零点定理可知至少存在一个ξ∈(1,2),使f(ξ)=0,故应选D.
14. 函数

的凹区间为______
- A.(1,e2)
- B.(0,1)
- C.(0,e2)
- D.(e2,+∞)
A B C D
A
[解析]

令y"=0,得x=e
2,当y">0时,1<x<e
2,故凹区间为(1,e
2),故应选A.
15. 导数

______
A.arcsinx
B.0
C.arcsinb-arcsina
D.

A B C D
B
[解析] 因为定积分

的值为常数,常数的导数等于0,所以

故应选B.
17. sin2x的一个原函数是______
A.2cos2x
B.

C.-cos
2x
D.

A B C D
C
[解析] 验证四个答案中哪个函数的导数是sin2x,(-cos2x)'=-2cosx·(cosx)'=2cosxsinx-sin2x.故应选C.
18. 设区域D由直线x=a,x=b(b>a),曲线y=f(x),y=g(x)围成,则区域D的面积为______
A.

B.

C.

D.

A B C D
D
[解析] 由定积分的几何意义可知,区域D的面积

故应选D.
19.

______
A.

B.

C.

D.

A B C D
B
[解析]

故应选B.
21. 微分方程xy"=y'的通解是______
A.y=C
1x+C
2 B.y=x
2+C
C.y=C
1x
2+C
2 D.

A B C D
C
[解析] 根据通解的概念首先排除B与D,现在对A、C进行验证后A不正确,故应选C.
24. 设
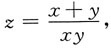
则dz=______
A.
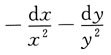
B.
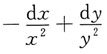
C.
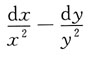
D.
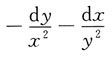
A B C D
A
[解析] 因为

所以

故应选A.
29. 正项级数

收敛的充分必要条件是______
A.

B.

C.

D.部分和数列有界
A B C D
D
[解析] 由正项级数收敛的基本准则知,正项级数收敛的充要条件是部分和数列有界,故应选D.
二、填空题1. 设

则f(0)=______.
2
[解析] 由f(x)的表达式可知,当x=0时,f(0)=2.
2.

[解析]

4. 设
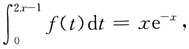
则f(x)=______.
[解析] 对

两边求导得
2f(2x-1)=e
-x-xe
-x=(1-x)e
-x,即

设t=2x-1则

代入得

所以

5.

x2ex-2xex+2ex+C
[解析]

6. 如果函数f(x)在区间[-2,2]上连续,且平均值为3,则

-12
[解析] 设f(x)的平均值为f(ξ),则

因此
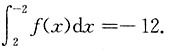
7. 设f(x+y,xy)=x
2+3xy+y
2+5,则f(x,y)=______.
x2+y+5
[解析] f(x+y,xy)=x2+3xy+y2+5=(x+y)2+xy+5,
所以f(x,y)=x2+y+5.
8. 方程

在空间直角坐标下表示的二次曲面是______.
椭球面
[解析]

空间直角坐标系下表示的曲面是椭球面.
9. 方程(y")
3-xy'+cosy=x
2+1是______阶微分方程.
二
[解析] 由微分方程的基本概念可知(y")3-xy'+cosy=x2+1是二阶微分方程.
10. 已知数项级数

收敛,则其和

三、计算题(每小题5分,共50分)
1. 求极限
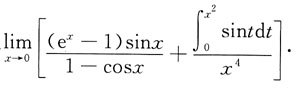
3.

4. 求定积分

5. 求过点(2,0,-3)且与直线
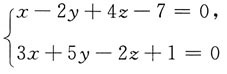
垂直的平面方程.
根据题意,所求平面的法向量可取已知直线的方向向量,即

故所求平面的方程为
-16(x-2)+14(y-0)+11(z+3)=0,
即16x-14y-11z-65=0.
6. 求函数f(x,y)=e
2x(x+y
2+2y)的极值.
解方程组

求得驻点为

f
xx=e
2x(4x+4y
2+8y+4),f
xy=e
2x(4y+4),f
yy=2e
2x,

由于B
2-AC=-4e
2<0,且A>0,
所以

为极小值点,函数的极小值为
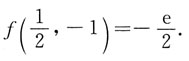
7. 在曲面z=xy上求一点,使这点处的法线垂直于平面x+3y+z+9=0,并写出法线方程.
设所求点为M(x
0,y
0,z
0),曲面在该点处的法向量为n={y
0,x
0,-1},平面的法向量为{1,3,1},
按题意,有

求得x
0=-3,y
0=-1,
z
0=x
0y
0=3,所以所求点为(-3,-1,3),
法线方程为

8. 设函数f(x)可微,且

求f(x).

两边分别对x求导,得
2f(x)-x=f'(x)且有f(0)=1,
即y'-2y=-x,y(0)=1,

将y(0)=1代入得

所以所求函数为

即
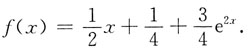
9. 求幂级数

的收敛半径与收敛域.
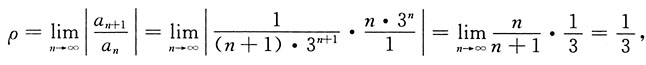
则收敛半径
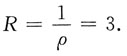
因此|x-1|<3,即-2<x<4,当x=-2时,幂级数化为

收敛,当x=4时,级数化为

发散,所以幂级数

的收敛域为[-2,4).
10. 求幂级数

的和函数.
五、证明题(6分)
1. 设f(x)在区间[a,b]上连续,在(a,b)上可导,且f(a)=f(b)=0.
证明:至少一点ξ∈(a,b)使f'(ξ)+2ξf(ξ)=0.
[证明] 设F(x)=f(x)ex2,则F(x)在[a,b]上连续,在(a,b)内可导,且
F(a)=f(a)ea2=0,F(b)=f(b)eb2=0,即F(a)=F(b),
所以至少存在一点ξ∈(a,b),使F'(ξ)=0,
即F'(ξ)=f'(ξ)eξ2+f(ξ)eξ2·2ξ=0,
又eξ2≠0,故f'(ξ)+2ξf(ξ)=0.
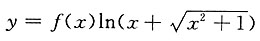 是______
是______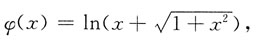
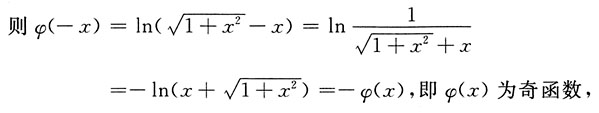
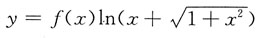 是偶函数,应选A.
是偶函数,应选A.
 ______
______


 故应选A.
故应选A. 则f(x)=______
则f(x)=______

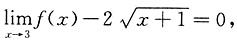 故f(3)=4,因此排除B、D选项,再将A、C代入原极限等式,可知C正确.
故f(3)=4,因此排除B、D选项,再将A、C代入原极限等式,可知C正确. 要使f(x)在(-∞,+∞)上连续,则a=______
要使f(x)在(-∞,+∞)上连续,则a=______
 根据连续的定义可知
根据连续的定义可知
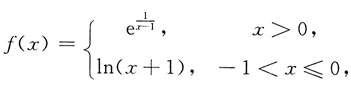 则x=0是f(x)______
则x=0是f(x)______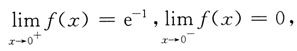 因此函数在x=0处左右极限存在但不相等,故x=0为跳跃间断点,故选C.
因此函数在x=0处左右极限存在但不相等,故x=0为跳跃间断点,故选C. 确定函数y(x)的二阶导数
确定函数y(x)的二阶导数 ______
______



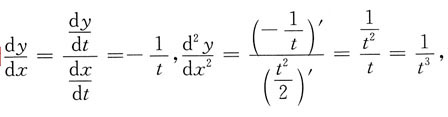 故应选B.
故应选B.



 故应选A.
故应选A.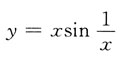 ______
______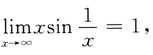 所以y=1为水平渐近线,
所以y=1为水平渐近线,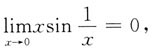 无垂直渐近线,故应选C.
无垂直渐近线,故应选C.

 的凹区间为______
的凹区间为______ 令y"=0,得x=e2,当y">0时,1<x<e2,故凹区间为(1,e2),故应选A.
令y"=0,得x=e2,当y">0时,1<x<e2,故凹区间为(1,e2),故应选A. ______
______
 的值为常数,常数的导数等于0,所以
的值为常数,常数的导数等于0,所以 故应选B.
故应选B.





 故应选D.
故应选D. ______
______




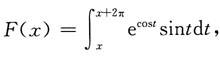 则F(x)______
则F(x)______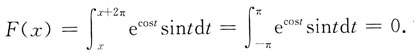 故应选C.
故应选C.
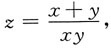 则dz=______
则dz=______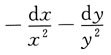
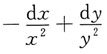
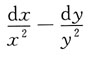
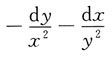

 故应选A.
故应选A.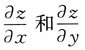 存在,则它在点(x0,y0)处______
存在,则它在点(x0,y0)处______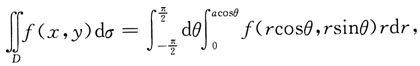 则区域D可表示为______
则区域D可表示为______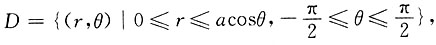 其积分区域的边界方程为r=acosθ,即x2+y2=ax,a>0,故应选D.
其积分区域的边界方程为r=acosθ,即x2+y2=ax,a>0,故应选D.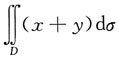 (其中D:|x|≤1,|y|≤1)=______
(其中D:|x|≤1,|y|≤1)=______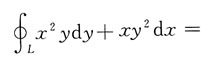 ______
______ 所以此曲线积分与路径无关,闭曲线积分为0,故应选D.
所以此曲线积分与路径无关,闭曲线积分为0,故应选D. 收敛的充分必要条件是______
收敛的充分必要条件是______


 在x=-1处收敛,则此级数在x=2处______
在x=-1处收敛,则此级数在x=2处______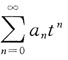 在t=-2处收敛,判断t=1处是否收敛的问题.根据阿贝尔定理可知,级数在t=1处绝对收敛,故应选B.
在t=-2处收敛,判断t=1处是否收敛的问题.根据阿贝尔定理可知,级数在t=1处绝对收敛,故应选B. 则f(0)=______.
则f(0)=______.
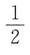

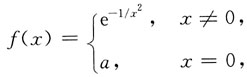 则
则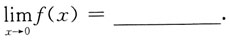
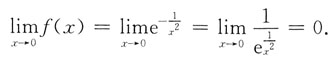
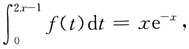 则f(x)=______.
则f(x)=______.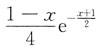
 两边求导得
两边求导得
 代入得
代入得




 因此
因此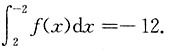
 在空间直角坐标下表示的二次曲面是______.
在空间直角坐标下表示的二次曲面是______. 空间直角坐标系下表示的曲面是椭球面.
空间直角坐标系下表示的曲面是椭球面. 收敛,则其和
收敛,则其和
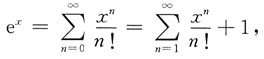
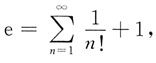 所以
所以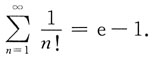
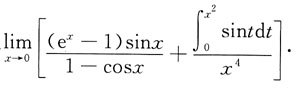
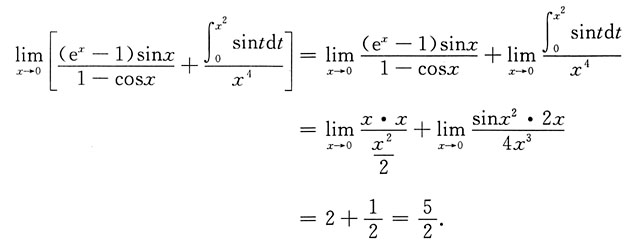
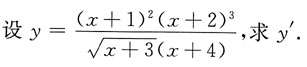
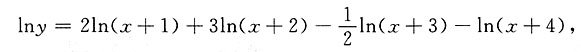
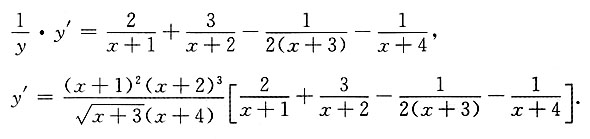



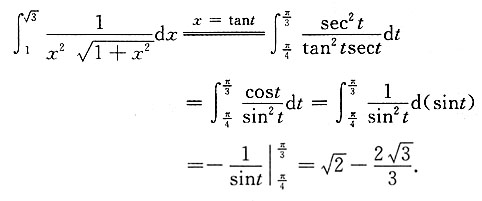
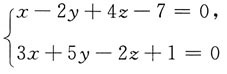 垂直的平面方程.
垂直的平面方程.



 为极小值点,函数的极小值为
为极小值点,函数的极小值为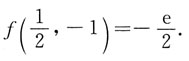
 求得x0=-3,y0=-1,
求得x0=-3,y0=-1,
 求f(x).
求f(x). 两边分别对x求导,得
两边分别对x求导,得


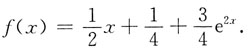
 的收敛半径与收敛域.
的收敛半径与收敛域.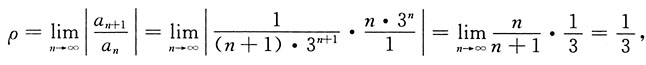 则收敛半径
则收敛半径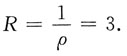
 收敛,当x=4时,级数化为
收敛,当x=4时,级数化为 发散,所以幂级数
发散,所以幂级数 的收敛域为[-2,4).
的收敛域为[-2,4). 的和函数.
的和函数.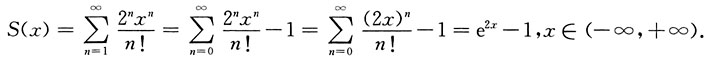
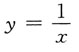 和直线y=x,x=2及x轴围成.求:
和直线y=x,x=2及x轴围成.求: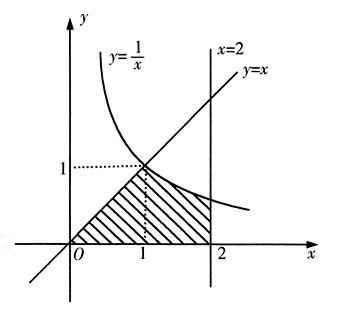
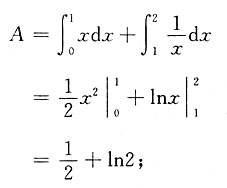
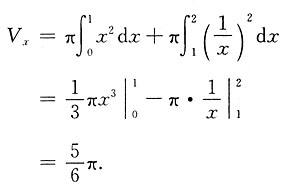
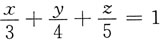 和柱面x2+y2=1的交线上与xOy平面距离最短的点.
和柱面x2+y2=1的交线上与xOy平面距离最短的点.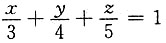 和x2+y2=1下的最小值问题:
和x2+y2=1下的最小值问题: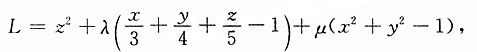
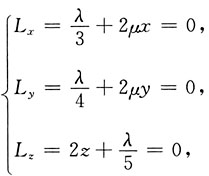 又由约束条件,有
又由约束条件,有
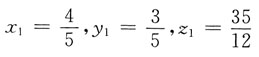 和
和 要使z2最小,显然应取
要使z2最小,显然应取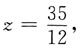 因此
因此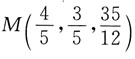 就是所求的点.
就是所求的点.