第Ⅰ部分 选择题
一、单项选择题(在每小题列出的四个选项中只有一个是符合题目要求的.)3. 交换积分顺序,则
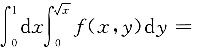
______
A.
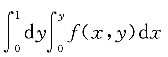
B.
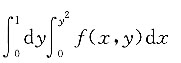
C.
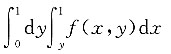
D.
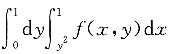
A B C D
D
[考点] 本题主要考查的知识点为交换积分顺序.
[解析] 由二重积分
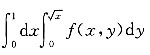
可知,积分区域D:0<x<1,
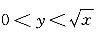
,如下图所示,故原积分
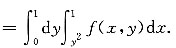
7. 设函数z=e
xy(x
2+y-1),则
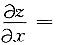
______
- A.exy(x2y+2x+y2)
- B.exy(x2y+2x+y2+y)
- C.exy(x2y+2x+y2-y)
- D.x2y-2x+y2-y
A B C D
C
[考点] 本题主要考查的知识点为函数的一阶偏导数.
[解析] 函数z=e
xy(x
2+y-1),则
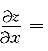
ye
xy(x
2+y-1)+e
xy(2x)=e
xy(X
2y+y
2-y)+2xe
xy=e
xy(x
2y+2x y
2-y).
8. 设∑为平面x+y+z=1,第一卦限中的部分,则对面积的曲面积分
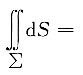
______
A.
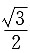
B.
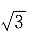
C.
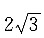
D.3
A B C D
A
[考点] 本题主要考查的知识点为面积的曲面积分.
[解析]
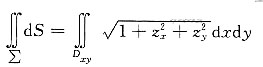
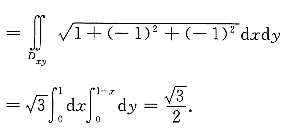
9. 已知y
1=e
x,y
2=x
2是微分方程y
'+P(x)y=Q(x)的两个特解,则Q(x)=______
A.
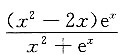
B.
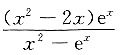
C.
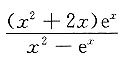
D.
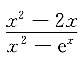
A B C D
B
[考点] 本题主要考查的知识点为微分方程的特解.
[解析] 将y
1=e
x,y
2=x
2代入微分方程y
'+P(-x)y=Q(x)得
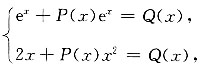
解方程组得
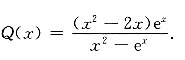
10. 无穷级数
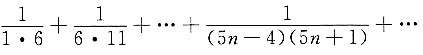
的和为______
A.1
B.
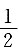
C.
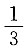
D.
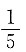
A B C D
D
[考点] 本题主要考查的知识点为无穷级数的和.
[解析]
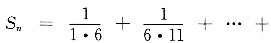
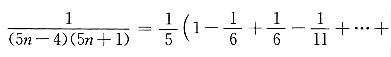
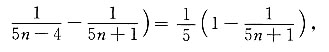

故所求无穷级数的和为
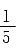
.
第Ⅱ部分 非选择题
二、计算题(每小题6分,共60分)1. 设函数z=f(e
xy,x+y),其中f是可微函数,求
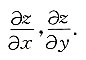
解:
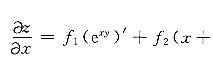
y)
'=ye
xyf
1+f
2,
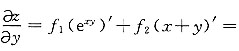
xe
xyf
1+f
2.
[考点] 本题主要考查的知识点为复合函数一阶求导.
2. 设函数f(x,y,z)=x
2+2y
2+2xyz,求f(x,y,z)在点P(-1,1,2)处的梯度.
解:
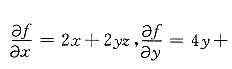
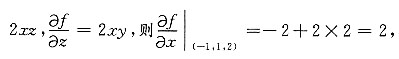
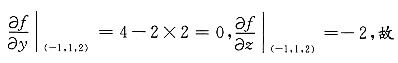
gardf(-1,1,2)={2,0,-2}.
[考点] 本题主要考查的知识点为函数的梯度.
3. 设函数z=ycosx,求
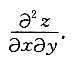
解:

[考点] 本题主要考查的知识点为函数的高阶偏导数.
4. 求曲面z=2x
2+y
2在点(1,1,3)处的切平面方程.
解:令F(x,y,z)=2x
2+
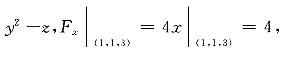
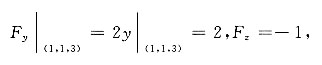
故所求切平面方程为4(x-1)+2(y-1)-(z-3)=0.
[考点] 本题主要考查的知识点为曲面的切平面方程.
5. 计算二重积分
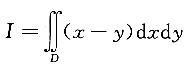
,其中D是由x+y=-1,x=0,y=0所围成的区域.
解:积分区域D,如下图所示,于是
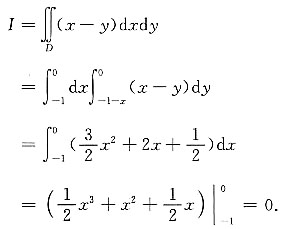
[考点] 本题主要考查的知识点为二重积分的计算.
6. 设Ω是由旋转抛物面z=x
2+y
2,平面z=0及平面z=1所围成的区域,求三重积分
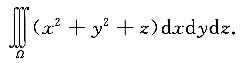
解:积分区域Ω,如下图所示.Ω在Oxy坐标面上的投影域为D
xy:x
2+y
2≤1,
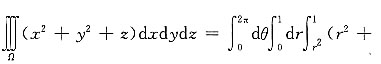
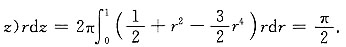
[考点] 本题主要考查的知识点为柱坐标下三重积分的计算.
7. 计算对弧长的曲线积分∫
L(x
2+y
2+z
2)ds,其中L为螺旋线x=cost,y=sint,z=2t(0≤t≤π)的一段.
解:∫
L(x
2+y
2+z
2)ds
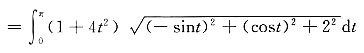
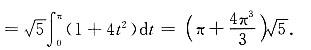
[考点] 本题主要考查的知识点为对弧长的曲线积分.
8. 求微分方程y
'=e
x-y满足初始条件y(0)=1的特解.
解:y'=ex-y,
即eydy=exdx
两边同时积分得ey=ex+C,
将初始条件y(0)=1代入得C=e-1,
故微分方程的特解为ey-ex-e=-1.
[考点] 本题主要考查的知识点为可分离变量微分方程求特解.
9. 判定级数
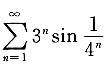
的收敛性.
解:由于当x>0时,sinx<x,所以

令
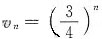
,又因为
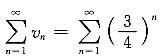
是等比级数,其中
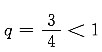
,故
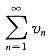
为收敛级数.
由比较判别法可知
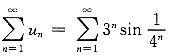
收敛.
[考点] 本题主要考查的知识点为无穷级数的敛散性(比较判别法).
10. 设函数f(x)=x
2(0≤x≤π)展开成为余弦级数为
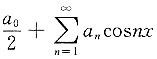
,求系数a
2.
解:
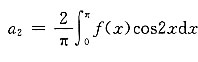
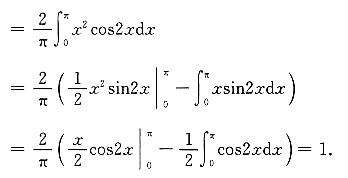
[考点] 本题主要考查的知识点为傅里叶系数.
三、综合题(每小题5分,共10分)1. 设矩形的周长为4,如何选取矩形的长和宽,能使得矩形的面积最大.
设矩形的长为x,宽为y,面积为S,则S=xy,x+y=2,
构造拉格朗日函数F(x,y,λ)=xy+λ(x+y-2),
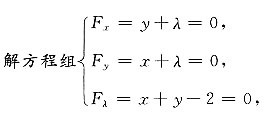
可得驻点x=1,y=1,λ=-1.
由于驻点唯一,且实际问题存在最大值,故(1,1)
是问题的最大值点,最大值为S=1.
[考点] 本题主要考查的知识点为条件极值.
2. 求平面2x+2y+z=4在第一卦限部分的面积.
设所求曲面∑的面积为S,∑在Oxy面上投影区域为D:x+y≤2,则有
∑:z=4-2x-2y,(x,y)∈D,故
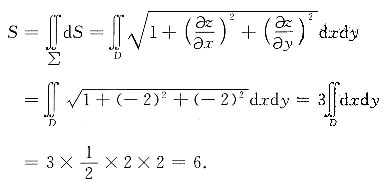
[考点] 本题主要考查的知识点为重积分的应用.