第Ⅰ部分 选择题
一、单项选择题(在每小题列出的四个选项中只有一个是符合题目要求的.)3. 设f(x)是连续函数,区域D:x
2+y
2≤4,则二重积分
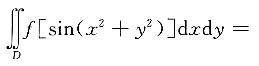
______
A.
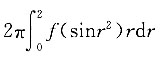
B.
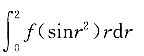
C.
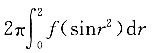
D.
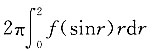
A B C D
A
[考点] 本题主要考查的知识点为二重积分的极坐标表示.
[解析]
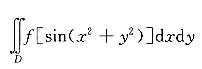
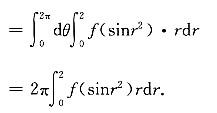
5. 下列无穷级数中,收敛的无穷级数是______
A.

B.
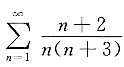
C.
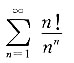
D.
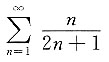
A B C D
C
[考点] 本题主要考查的知识点为判断级数的敛散性.
[解析] 对于选项
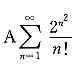
,由于
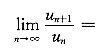
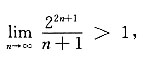
故此级数发散;对于选项B
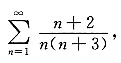
由于
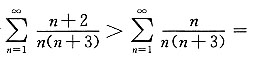
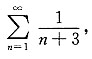
而
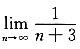
发散,故

也发散;对于选项D
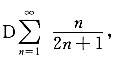
由于
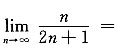
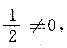
故选项D也发散;选项
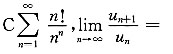
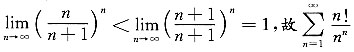
收敛.
6. 在空间直角坐标系中,Oxy平面上的曲线
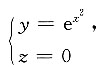
绕y轴旋转的旋转曲面方程为______
- A.y=ex2+z2
- B.y=ex2+y2
- C.y=(x2+z2)ex2+z2
- D.y=x2ex2+z2
A B C D
A
[考点] 本题主要考查的知识点为旋转曲面.
[解析] 曲线绕y轴旋转,则y不变,将x换成
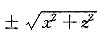
,从而得旋转曲面的方程为y=e
x2+z2.
此类旋转,可简记为绕谁旋转,谁就不变.
8. 设二次积分
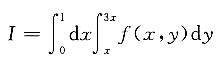
,则交换积分次序得I=______
A.
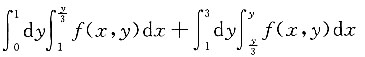
B.
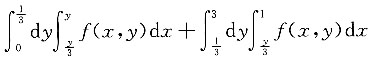
C.
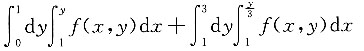
D.
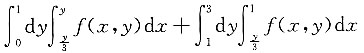
A B C D
D
[考点] 本题主要考查的知识点为二重积分交换积分次序.
[解析] 将区域D分成两个小区域D
1与D
2,如下图所示.
即D=D
1+D
2 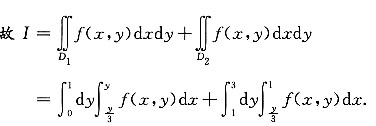
10. 设f(x)=xln(1+x)展成x幂级数为

,则系数a
2=______
A.
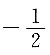
B.-1
C.0
D.

A B C D
A
[考点] 本题主要考查的知识点为幂级数的展开式.
[解析] 由
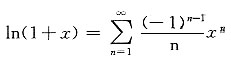
得
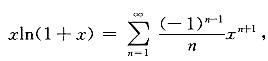
则
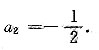
第Ⅱ部分 非选择题
二、计算题(每小题6分,共60分)1. 已知原点在平面π上的投影点P的坐标为(2,9,-6),求此平面方程.
解:由题意可知OP⊥平面π,向量
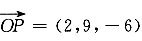
,即所求平面π过点(2,9,-6)且平面π的法向量n={2,9,-6},故所要求的平面π的方程为2(x-2)+9(y-9)-6(z+6)=0,即2x+9y-6z-121=0.
[考点] 本题主要考查的知识点为平面方程的求法.
2. 已知函数z=ysinx,求全微分dz.
解:zx=ycosx,zy=sinx,则所求的全微分dz=ycosxdx+sinxdy.
[考点] 本题主要考查的知识点为全微分.
3. 求函数f(x,y,z)=x
2yz+yz在点(-1,2,1)处的梯度.
4. 求空间曲线x=t
3,y=2t,z=t
2-t在点(1,2,0)处的法平面方程.
解:由题意知t=1,则
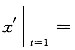
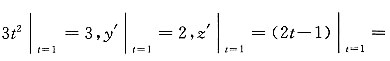
1,故所求的法平面方程为3(x-1)+2(y-2)+z=0.
[考点] 本题主要考查的知识点为空间曲线的法平面方程.
5. 设D是由x
2+y
2=π
2与x
2+y
2=4π
2所围成的区域,求二重积分
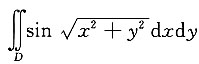
.
解:令x=rcosθ,y=rsinθ且0≤θ≤2π,π≤r≤2π,所以
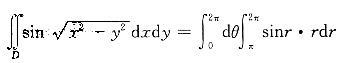
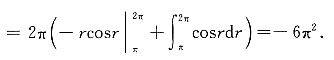
[考点] 本题主要考查的知识点为用极坐标计算二重积分.
6. 计算三重积分
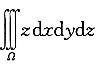
,其中Ω:0≤x≤1,
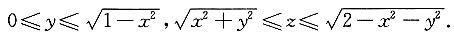
解:

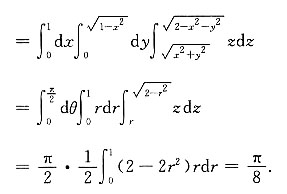
[考点] 本题主要考查的知识点为用柱面坐标计算三重积分.
7. 计算对坐标的曲线积分
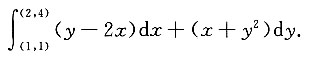
解:令P(x,y)=y-2x,Q(x,y)=x+y
2,则
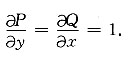
于是选择积分曲线对折线ABC,如下图所示.
在AB段,y=1,dy=0,在BC段,x=2,dx=0,
则
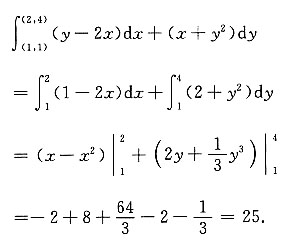
[考点] 本题主要考查的知识点为平面曲线积分与路径无关的条件.
8. 求微分方程
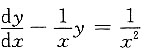
的通解.
解:由一阶线性微分方程的通解公式有
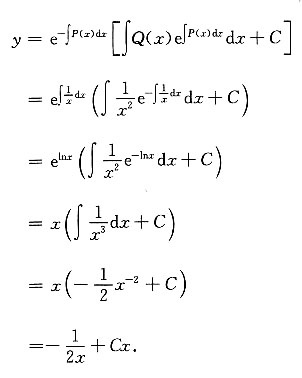
注意公式中对P(x)积分的正负号,且此题
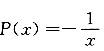
而非
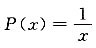
.另此题还可以用常数变易法.
[考点] 本题主要考查的知点为一阶线性微分方程解.
9. 求无穷级数
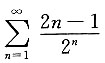
的和.
10. 求幂级数1+2x+3x
2+…+nx
n-1+…的和函数.
解:令a
n=n,由
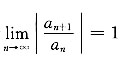
得级数的收敛半径R=1,又x=±1时原级数均发散,则原级数的收敛域为(-1,1),设S(x)=
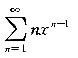
x∈(-1,1),逐项求积得

[考点] 本题主要考查的知识点为幂级数的和函数.
三、综合题(每小题5分,共10分)1. 验证在整个Oxy平面内(x
2+2xy+y
2)dx+(x
2+2xy-y
2)dy是某个二元函数u(x,y)的全微分,并求这样的一个u(x,y).
令P(x,y)=x
2+2xy+y
2,Q(x,y)=x
2+2xy-y
2,
由于
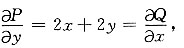
在Oxy平面内处处成立,所以(x
2+2xy+y
2)dx+(x
2+2xy-y
2)dy是某个二元函数u(x,y)的全微分.
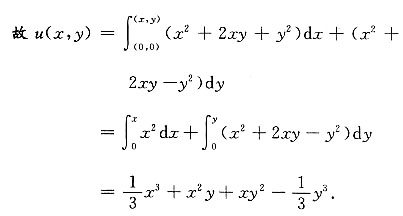
[考点] 本题主要考查的知识点为二元函数的全微分求积.
2. 设f(x)是以2π为周期函数,它在(-π,π)上的表达式为
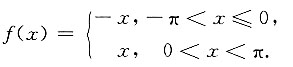
求f(x)的傅里叶级数展开式.
[考点] 本题主要考查的知识点为傅里叶级数展开式.