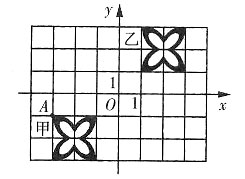
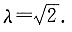一、单项选择题3. 已知点P(a+1,2a-3)关于x轴的对称称点在第一象限,则a的取值范围是______
A.a<-1
B.
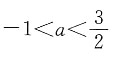
C.
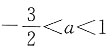
D.

A B C D
B
[解析] 点P(a+1,2a-3)关于x轴的对称点的坐标为(a+1,-2a+3).∵这个对称点在第一象限,
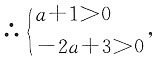
解这个不等式组,得
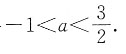
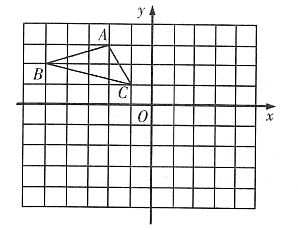
5. 如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),△ABC向右平移4个单位得到△A
1B
1C
1,再作△A
1B
1C
1关于x轴的对称图形△A
2B
2C
2,则顶点A
2的坐标是______
- A.(-3,2)
- B.(2,-3)
- C.(1,-2)
- D.(3,-1)
A B C D
B
[解析] 把△ABC向右平移4个单位长度,则点A的横坐标为-2+4=2,纵坐标不变,即A1(2,3);作△A1B1C1关于x轴的对称图形,则点A1的横坐标不变,纵坐标为3×(-1)=-3,即A2(2,-3).
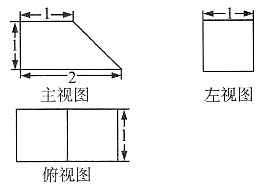
10. 将一个棱长为a的正方体,切成27个全等的小正方体,则表面积增加了______
A B C D
B
[解析] 每个小正方体的棱长为
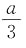
,表面积为
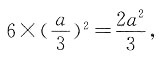
所以所有小正方体的表面积和为
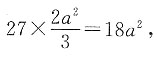
所以表面积增加了18a
2-6a
2=12a
2,所以选B.
11. 一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积的比为______
A.
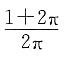
B.
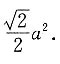
C.
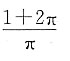
D.
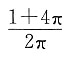
A B C D
A
[解析] 设底面半径为r,则侧面积为4π
2r
2,表面积为4π
2r
2+2πr
2,表面积与侧面积的比为
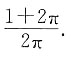
13. 一个球与它的外切圆柱、外切等边圆锥(圆锥的轴截面为正三角形)的体积之比______
- A.2:3:5
- B.2:3:4
- C.3:5:8
- D.4:6:9
A B C D
D
[解析] 作出轴截面,圆内切于一个正方形和一个等边三角形,易知正方形的边长等于圆的直径,圆心是等边三角形的中心,设球的半径为r,则外切圆柱的底面圆的半径为r,高为2r,外切圆锥的底面圆的半径为

高为3r,所以球的体积
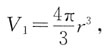
外切圆柱的体积V
2=πr
2×2r=2πr
3,外切等边圆锥的体积
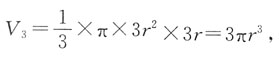
所以

所以选D.
14. 在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是______
A.
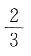
B.
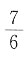
C.
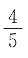
D.
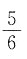
A B C D
D
[解析] 因为截去的这8个三棱锥的体积相等,都为
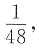
所以余下的多面体的体积为
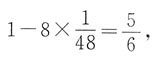
所以选D.
22. 以下条件中能够推出平面α//平面β的个数为______
①平面α内有两条直线a,b,且a//β,b//β;
②平面α内有无数条直线与平面β平行;
③平面α内不存在与平面β有公共点的直线;
④平面α内不共线的三点到平面β的距离相等;
⑤平面α内任意一条直线平行于平面β.
A B C D
B
[解析] 根据面面平行的判定定理,①中α内的直线a,b可以是平行的,所以错误;②中的直线可以是平面α中的平行直线,所以错误;③即说明两平面没有公共点,所以正确;④三点可以在平面β的两侧,所以错误;⑤中任意的直线当然存在相交直线,所以选B.
26. 已知点A(-3,1,5)和点B(4,3,1),则线段AB的中点坐标是______
A.
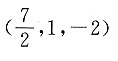
B.
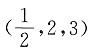
C.(-12,3,5)
D.
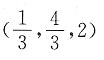
A B C D
B
[解析] 设A,B的中点C(x,y,z),则
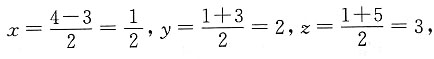
所以
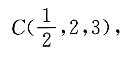
所以选B.
二、填空题1. 正方形绕其中心旋转一定的角度与原图形重合,则这个角至少为______度.
90
[解析] ∵正方形的对角线把正方形分成四个全等的直角三角形,∴正方形绕着它的中心旋转90°的整教倍后,就能与它自身重合,因此,这个角至少是90度.
2. 如图,将等边三角形ABC沿BC方向平移得到△A
1B
1C
1.
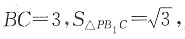
则BB
1=______.
1
[解析] 如图,过P作PD⊥B
1C于点D.∵将等边三角形ABC沿BC方向平移得到△A
1B
1C
1,∴∠PB
1C=∠ACB=60°,∴∠CPB
1=60°,∴△PCB
1是等边三角形.设等边三角形PCB
1的边长是2a,则B1
D=CD=a,由勾股定理得:PD=
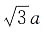
.
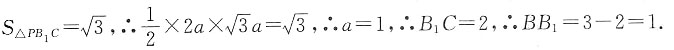
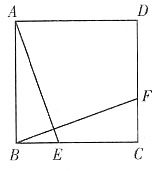
3. 如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则α=______°.
90
[解析] 以正方形ABCD的中心为旋转中心,△ABE旋转到△BCF,恰好旋转了90°.
4. 一个底面边长为
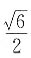
,侧棱长为
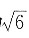
的正六棱柱的所有顶点都在一个球面上,则此球的体积为______.
[解析] 球的直径等于正六棱柱的体对角线长,设球的半径为R,由已知可得
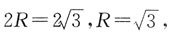
所以球的体积为
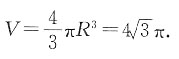
5. 在空间直角坐标系中,正方体ABCD-A
1B
1C
1D
1的顶点A(3,-1,2),其中心为M(0,1,2),则该正方体的棱长为______.
[解析] 设该正方体的棱长为a,因为
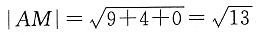
为正方体体对角线长的一半,所以
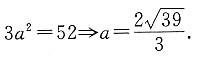
6. 动点M(x,y,z)在面z=0与面x+y=0的交线上,定点A(1,1,1),则|AM|的最小值为______.
[解析] 由题意设点M(x,-x,0),则
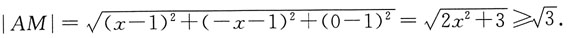
7. 已知平行四边形ABCD的顶点A(4,1,3),B(2,-5,1),C(3,7,-5),则顶点D的坐标是______.
D(5,13,-3)
[解析] 因为平行四边形的对角线互相平分,所以AC的中点为
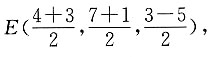
即
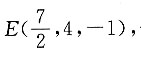
设点D(x,y,z)则点E是BD的中点,所以
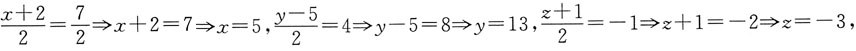
所以D(5,13,-3).
三、简答题1. 有一根旗杆AB高8m,它的顶端A处挂一条长10m的绳子,拉紧绳子并分别把它的下端放在地面上的两点C,D(B,C,D三点不共线)处,如果这两点和旗杆脚B处的距离都是6m,那么旗杆就和地面垂直,为什么?
如图,在△ABC和△ABD中,
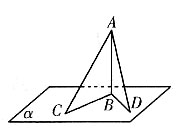
因为AB=8m,BC=BD=6m,AC=AD=10m,
所以AB
2+BC
2=6
2+8
2=10
2=AC
2,AB
2+BD
2=6
2+8
2=10
2=AD
2,
所以∠ABC=∠ABD=90°,即AB⊥BC,AB⊥BD,又因为B,C,D不共线,
所以AB⊥平面BCD,即旗杆和地面垂直.
2. 如图所示,已知空间四边形ABCD,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且
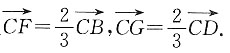
求证:四边形EFGH是梯形.
∵E,H分别是边AB,AD的中点,

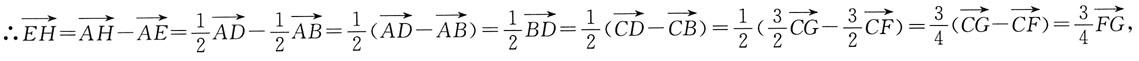
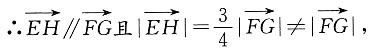
又F不在EH上,∴四边形EFGH是梯形.
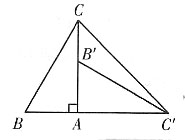
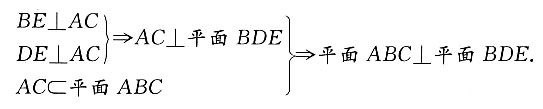
3. 证明:MN//平面A'ACC';
如图所示,连接AB',AC',因为三棱柱ABC—A'B'C'为直三棱柱,所以四边形ABB'A'为矩形,
又M为A'B的中点,所以M为AB'的中点.
又N为B'C'的中点,所以MN//AC'.
因为

平面A'ACC',

平面A'ACC',
所以MN//平面A'ACC'.
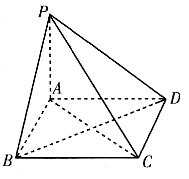
4. 若二面角A'—MN—C为直二面角,求λ的值.
以A为坐标原点,分别以直线AB,AC,AA'为x轴,y轴,z轴建立如上图所示的空间直角坐标系Axyz.设AA'=1,则AB=AC=λ,
于是A(0,0,0),B(λ,0,0),C(0,λ,0),A'(0,0,1),B'(λ,0,1),C'(0,λ,1),
所以
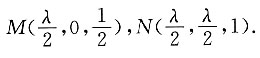
设m=(x
1,y
1,z
1)是平面A'MN的一个法向量,
由
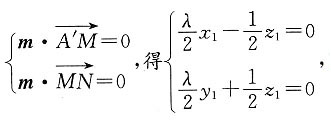
可取m=(1,-1,λ).
设n=(x
2,y
2,z
2)是平面MNC的一个法向量,
由
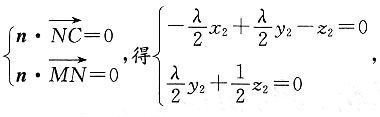
可取n=(-3,-1,λ).
因为A'—MN—C为直二面角,所以m·n=0,即-3+1+λ
2=0,解得
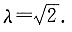
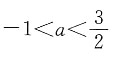
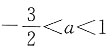

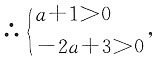 解这个不等式组,得
解这个不等式组,得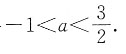
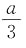 ,表面积为
,表面积为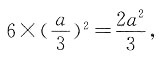 所以所有小正方体的表面积和为
所以所有小正方体的表面积和为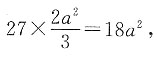 所以表面积增加了18a2-6a2=12a2,所以选B.
所以表面积增加了18a2-6a2=12a2,所以选B.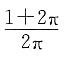
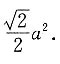
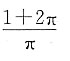
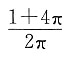
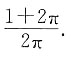
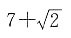
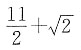
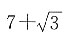

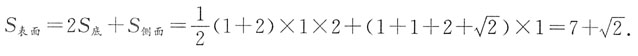
 高为3r,所以球的体积
高为3r,所以球的体积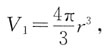 外切圆柱的体积V2=πr2×2r=2πr3,外切等边圆锥的体积
外切圆柱的体积V2=πr2×2r=2πr3,外切等边圆锥的体积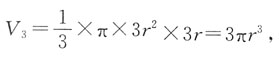 所以
所以 所以选D.
所以选D.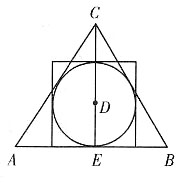
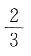
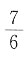
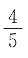
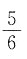
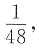 所以余下的多面体的体积为
所以余下的多面体的体积为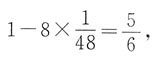 所以选D.
所以选D.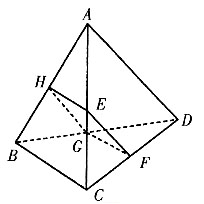
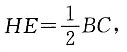 同理
同理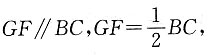
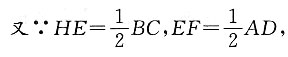 AD=BC,所以EF=HE,所以四边形EFGH是菱形.
AD=BC,所以EF=HE,所以四边形EFGH是菱形.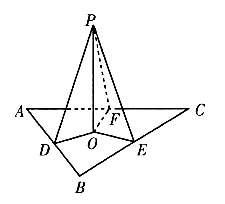
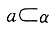 的情况,所以选C.
的情况,所以选C.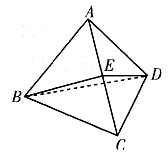
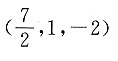
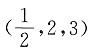
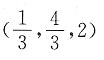
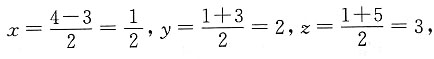 所以
所以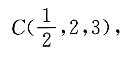 所以选B.
所以选B. 则BB1=______.
则BB1=______.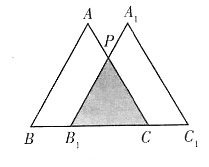
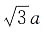 .
.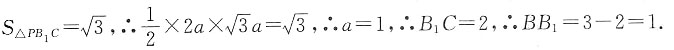
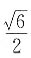 ,侧棱长为
,侧棱长为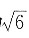 的正六棱柱的所有顶点都在一个球面上,则此球的体积为______.
的正六棱柱的所有顶点都在一个球面上,则此球的体积为______.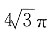
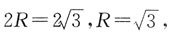 所以球的体积为
所以球的体积为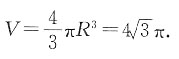
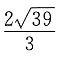
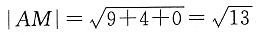 为正方体体对角线长的一半,所以
为正方体体对角线长的一半,所以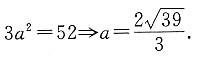
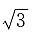
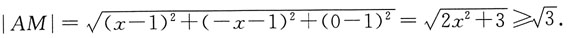
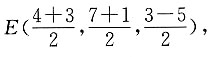 即
即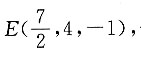 设点D(x,y,z)则点E是BD的中点,所以
设点D(x,y,z)则点E是BD的中点,所以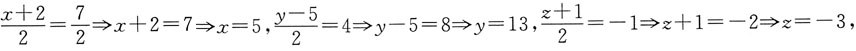 所以D(5,13,-3).
所以D(5,13,-3).
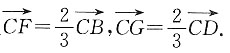 求证:四边形EFGH是梯形.
求证:四边形EFGH是梯形.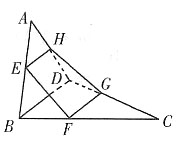

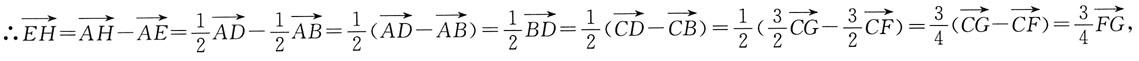
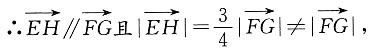 又F不在EH上,∴四边形EFGH是梯形.
又F不在EH上,∴四边形EFGH是梯形.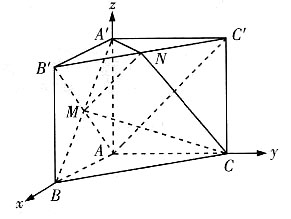
 平面A'ACC',
平面A'ACC', 平面A'ACC',
平面A'ACC',
 可取m=(1,-1,λ).
可取m=(1,-1,λ). 可取n=(-3,-1,λ).
可取n=(-3,-1,λ).