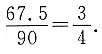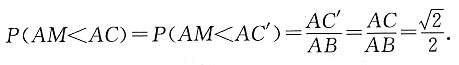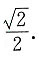一、单项选择题3. 若直线x-y=2被圆(x-a)
2+y
2=4所截得的弦长为

,则实数a的值为______
A.
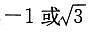
B.1或3
C.-2或6
D.0或4
A B C D
D
[解析] 圆心(a,0)到直线x-y=2的距离
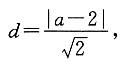
则
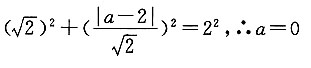
或a=4,故选D.
4. 直线
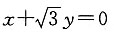
绕原点按顺时针方向旋转30°所得直线与圆x
2+y
2-4x+1=0的位置关系是______
- A.直线与圆相切
- B.直线与圆相交但不过圆心
- C.直线与圆相离
- D.直线过圆心
A B C D
A
[解析] ∵直线
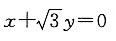
的倾斜角为150°,∴按顺时针方向旋转30°后的倾斜角为120°,
∴旋转后的直线方程为
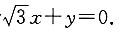
将圆的方程化为(x-2)
2+y
2=3,
∴圆心的坐标为(2,0),半径为

圆心到直线
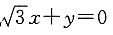
的距离为
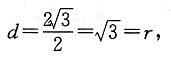
∴直线和圆相切,故选A.
5. 圆C
1:x
2+y
2+2x+2y-2=0与圆C
2:x
2+y
2-4x-2y+4=0的公切线有______
A B C D
D
[解析] 圆C
1:(x+1)
2+(y+1)
2=4,∴圆心C
1(-1,-1),半径长r
1=2;
圆C
2:(x-2)
2+(y-1)
2=1,∴圆心C
2(2,1),半径长r
2=1.
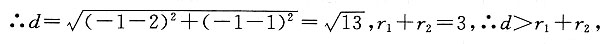
∴两圆外离,∴两圆有4条公切线.
6. 若动圆C与圆C
1:(x+2)
2+y
2=1及圆C
2:(x-2)
2+y
2=4分别相切,且一个内切,一个外切,则动圆C的圆心的轨迹是______
- A.两个椭圆
- B.一个椭圆及一个双曲线的一支
- C.两个双曲线的各一支
- D.一个双曲线的两支
A B C D
D
[解析] 设动圆C的半径为r,依题意得|C1C|=r-1,|C2C|=r+2或|C1C|=r+1,|C2C|=r-2,所以|C2C|-|C1C|=3或|C1C|-|C2C|=3,故C点的轨迹为一个双曲线的两支,故选D.
7. 若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是______
A.
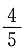
B.
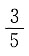
C.
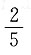
D.
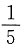
A B C D
B
[解析] 依题意有2×2b=2a+2c,即2b=a+c,所以4b
2=a
2+2ac+c
2,
∵b
2=a
2-c
2,∴4a
2-4c
2=a
2+2ac+c
2,
∴3a
2-2ac-5c
2=0,两边同除以a
2,即有5e
2+2e-3=0,解得
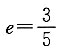
或e=-1(舍去),故选B.
8. 若椭圆上存在点P到两个焦点的距离之比为2:1,则此椭圆离心率的取值范围是______
A.
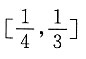
B.
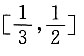
C.
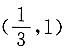
D.
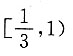
A B C D
D
[解析] 设P到两个焦点的距离分别是2k,k(k>0),根据椭圆定义可知3k=2a,又结合椭圆的性质可知,椭圆上的点到两焦点距离之差的最大值为2c,即k≤2c,∴2a≤6c,即
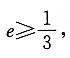
故选D.
9. 已知以F
1(-2,0),F
2(2,0)为焦点的椭圆与直线
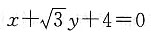
有且仅有一个交点,则椭圆的长轴长为______
A.
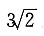
B.

C.
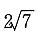
D.
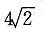
A B C D
C
[解析] 设椭圆方程为
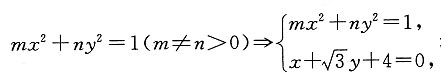
消去x得:
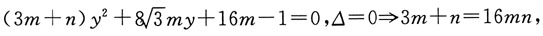
即:
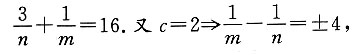
联立解得
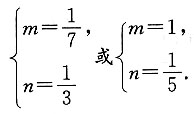
由焦点在x轴上,所以
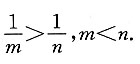
所以
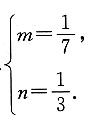
故长轴长为
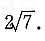
12. 已知抛物线y
2=2px(p>0)的准线与圆(x-3)
2+y
2=16相切,则实数p的值为______
A.
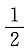
B.1
C.2
D.4
A B C D
C
[解析] 抛物线y
2=2px(p>0)的准线方程为
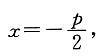
因为抛物线y
2=2px(p>0)的准线与圆(x-3)
2+y
2=16相切,所以
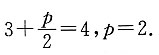
17. 为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
| 父亲身高x(cm) | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y(cm) | 175 | 175 | 176 | 177 | 177 |
则y对x的线性回归方程为______
A.y=x-1
B.y=x+1
C.
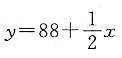
D.y=176
A B C D
C
[解析]

18. 设(x
1,y
1),(x
2,y
2),…,(x
n,y
n)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论正确的是______
A.直线l过点

B.x和y的相关系数为直线l的斜率
C.x和y的相关系数在0到1之间
D.当n为偶数时,分布在l两侧的样本点的个数一定相同
A B C D
A
[解析] 对于B,因x和y的相关系数与直线l的斜率的求法、定义均不同,故它们不一定相等.
从图形可看出x和y负相关,相关系数小于零,故C不正确,样本点应大部分在直线l附近,不一定在l两侧的数目相同,故D错误.
二、简答题1. 求直线xsin θ+ycos θ+1=0(其中
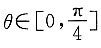
)的倾斜角的取值范围.
原直线可化为
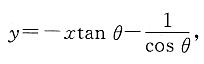
因此直线的斜率为
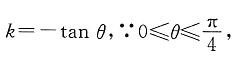
∴0≤tan θ≤1,∴-1≤-tan θ≤0,即-1≤k≤0,设直线的倾斜角为α,
则-1≤tan α≤0,故
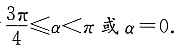
2. 求证:无论a为何值,直线l总过第三象限;
由l:ay=(3a-1)x-1,得a(3x-y)+(-x-1)=0,由
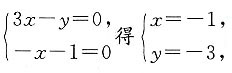
所以直线l过定点(-1,-3),因此直线总过第三象限.
3. a取何值时,直线l不过第二象限?
作图可知,应有斜率
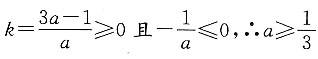
时直线l不过第二象限.
4. 已知直线l
1:3mx+8y+3m-10=0和l
2:x+6my-4=0.问m为何值时:
(1)l
l与l
2相交;
(2)l
1与l
2平行;
(3)l
1与l
2垂直.
当m=0时,l
1:8y-10=0;l
2:x-4=0,l
1与l
2垂直;
当m≠0时,
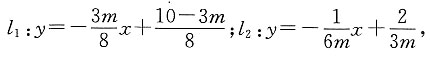
由
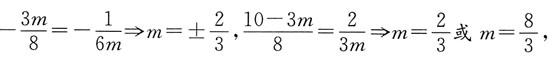
而
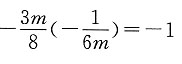
无解.
综上所述(1)
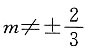
时,l
1与l
2相交;(2)
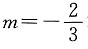
时,l
1与l
2平行;(3)m=0时,l
1与l
2垂直.
5. l
1与l
2相交于点P(m,-1);
∵m2-8+n=0且2m-m-1=0,∴m=1,n=7.
6. l
1//l
2.
由m·m-8×2=0,得m=±4,由8×(-1)-n·m≠0,得n≠±2,
即m=4,n≠-2时或m=-4,n≠2时,l1//l2.
7. 若点A(5,0)到l的距离为3,求l的方程;
经过两已知直线交点的直线系方程为(2x+y-5)+λ(x-2y)=0,
即(2+λ)x+(1-2λ)y-5=0,∴
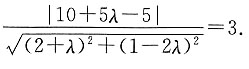
即2λ
2-5λ+2=0,
∴λ=2或
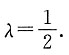
∴l的方程为x=2或4x-3y-5=0.
8. 求点A(5,0)到l的距离的最大值.
由
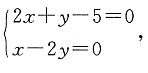
解得交点P(2,1),过P作任一直线l,设d为点A到l的距离,则d≤|PA|(当l⊥PA时等号成立).
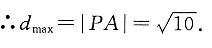
9. 求经过点A(5,2),B(3,2),圆心在直线2x-y-3=0上的圆的方程;
设圆心C(a,b),则有
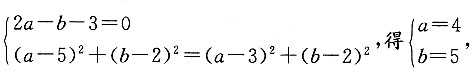
∴半径
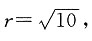
所求圆的方程为(x-4)
2+(y-5)
2=10.
10. 求以O(0,0),A(2,0),B(0,4)为顶点的三角形OAB外接圆的方程.
设圆的方程为x
2+y
2+Dx+Ey+F=0,将三个已知点的坐标代入得
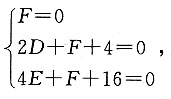
解得
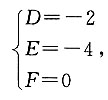
故所求圆的方程为x
2+y
2-2x-4y=0.
11. 求圆C:(x+2)
2+(y+3)
2=1关于直线x+y+2=0对称的圆的方程.
解法一 设圆心C(-2,-3)关于直线x+y+2=0的对称点为C'(x
0,y
0),
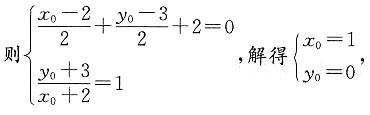
所以C'(1,0),故所求的圆方程为(x-1)
2+y
2=1.
解法二 设对称圆上任一点P(x,y),其关于直线x+y+2=0的对称点P'(x
0,y
0)一定在已知圆上,
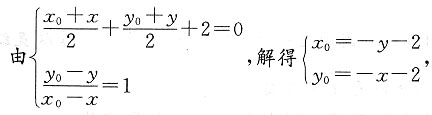
代入已知圆的方程,得(x-1)
2+y
2=1.
12. 已知圆(x-2)
2+y
2=1,求:
(1)x
2+y
2的最大值;
(2)
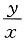
的最大值与最小值;
(3)x-2y的最小值.
设x-2y=t,则x=2y+t,代入圆的方程并化简得5y
2+4(t-2)y+t
2-4t+3=0,
∴Δ=16(t-2)
2-20(t
2-4t+3)≥0,解得
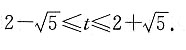
13. 已知圆的方程x
2+y
2=2,直线y=x+b,当b为何值时,圆与直线
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点.
解法一 圆心O(0,0)到直线y=x+b的距离为

圆的半径
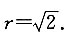
(1)当d<r,即-2<b<2时,直线与圆相交,有两个公共点;
(2)当d=r,即b=±2时,直线与圆相切,有一个公共点;
(3)当d>r,即b>2或b<-2时,直线与圆相离,无公共点.
解法二 联立两个方程得方程组
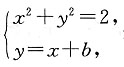
消去y得,2x
2+2bx+b
2-2=0,Δ=16-4b
2.
(1)当Δ>0,即-2<b<2时,有两个公共点;
(2)当Δ=0,即b=±2时,有一个公共点;
(3)当Δ<0,即b>2或b<-2时,无公共点.
14. 实数k为何值时,两圆C
1:x
2+y
2+4x-6y+12=0,C
2:x
2+y
2-2x-14y+k=0相切?
将两圆的方程化为标准式:C
1:(x+2)
2+(y-3)
2=1,C
2:(x-2)
2+(y-7)
2=50-k,圆C
1的圆心C
1(-2,3),半径r
1=1,圆C
2的圆心C
2(1,7),半径
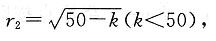
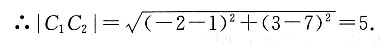
当两圆外切时,|C
1C
2|=r
1+r
2,即
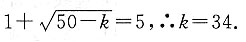
当两圆内切时,|C
1C
2|=|r
1-r
2|,即
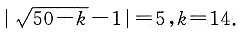
∴两圆相切时,k的值为34或14.
 的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为
的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为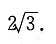
15. 求椭圆C的焦距;
由已知可得F
1到直线l的距离

故c=2,所以椭圆C的焦距为4.
16. 如果
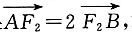
求椭圆C的方程.
设A(x
1,y
1),B(x
2,y
2),不妨令y
1<0,y
2>0,
由题意得直线l的方程为
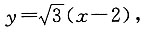
联立
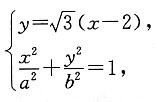
得
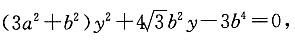
解得
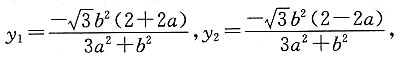
因为
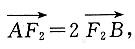
所以-y
1=2y
2,即
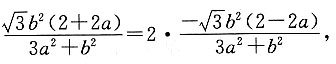
得a=3,而a
2-b
2=4,所以b
2=5,故椭圆C的方程为
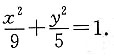
17. 与双曲线
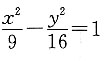
有共同的渐近线,且过点
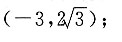
经检验知双曲线的焦点在x轴上,故设双曲线的方程为
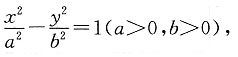
由题意得
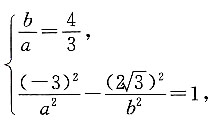
解得
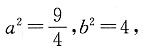
所以双曲线的方程为
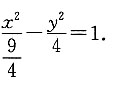
18. 与双曲线

有公共焦点,且过点
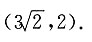
设双曲线方程为
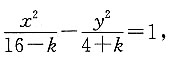
且16-k>0,4+k>0.
将点
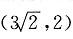
代入得k=4,且满足上面的不等式,所以双曲线方程为
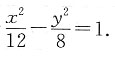
19. 已知动圆M与圆C
1:(x+4)
2+y
2=2外切,与圆C
2:(x-4)
2+y
2=2内切,求动圆圆心M的轨迹方程.
设动圆M的半径为r,
则由已知
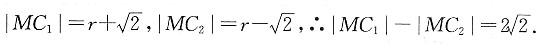
又
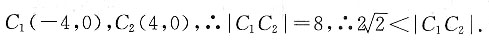
根据双曲线定义知,点M的轨迹是以C
1(-4,0),C
2(4,0)为焦点的双曲线的右支.
又
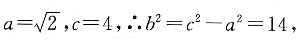
∴点M的轨迹方程是
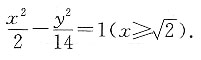
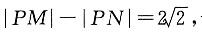 记动点P的轨迹为W.
记动点P的轨迹为W.20. 求W的方程;
由
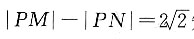
知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长
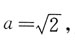
又半焦距c=2,故虚半轴长
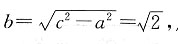
所以W的方程为
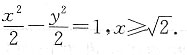
21. 若A,B是W上的不同两点,O是坐标原点,求
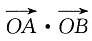
的最小值.
设A,B的坐标分别为(x
1,y
1),(x
2,y
2),当AB⊥x轴时,x
1=x
2,从而y
1=-y
2,从而
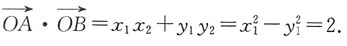
当AB与x轴不垂直时,设直线AB的方程为y=kx+m,与W的方程联立,消去y得(1-k
2)x
2-2kmx-m
2-2=0.故
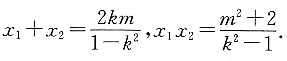
所以

=x
1x
2+y
1y
2=x
1x
2+(kx
1+m)(kx
2+m)=(1+k
2)x
1x
2+km(x
1+x
2)+m
2=
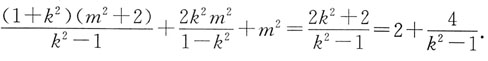
又因为x
1x
2>0,所以k
2-1>0,从而
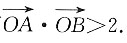
综上,当AB⊥x轴时,
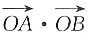
取得最小值2.
22. 求抛物线方程;
抛物线y
2=2px(p>0)的准线方程为
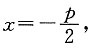
于是
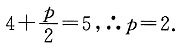
∴抛物线的标准方程为y
2=4x.
23. 过M作MN⊥FA,垂足为N,求点N的坐标.
由(1)得点A的坐标是(4,4),由题意得B(0,4),M(0,2),
又F(1,0),

则FA所在直线的方程为

MN所在直线的方程为
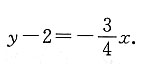
解方程组

24. 某高中有高级教师6人,中级教师12人,初级教师18人,要从这些人中抽取一个容量为n的样本.如果采用系统抽样法和分层抽样法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要从总体中先剔除1个个体.求样本容量n.
总体容量为6+12+18=36(人).当样本容量是n时,由题意知:系统抽样的间隔为
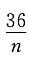
,分层抽样的比例是
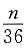
,抽取高级教师
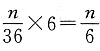
人,抽取中级教师
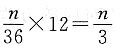
人,抽取初级教师
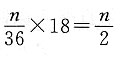
人.所以n应是6的倍数,36的约数,即n值可为6,12,18,36.
当样本容量为(n+1)时,总体中剔除1个是35人,系统抽样的间隔为
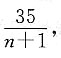
因为
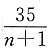
必须是整数,所以n只能取6,即样本容量n=6.
25. 某工厂甲、乙两名工人参加操作技术培训,他们在培训期间参加的8次测试成绩记录如下:
| 甲 | 95 | 82 | 88 | 81 | 93 | 79 | 84 | 78 |
| 乙 | 83 | 92 | 80 | 95 | 90 | 80 | 85 | 75 |
试比较哪个工人的成绩较好.
26. 巴西医生马廷收集了贪官与廉洁官员的寿命的调查资料:500名贪官中有348人的寿命小于平均寿命,152人的寿命大于或等于平均寿命;590名廉洁官员中有93人的寿命小于平均寿命,497人的寿命大于或等于平均寿命.这里的平均寿命是指“当地人均寿命”.试分析官员在经济上是否清白与他们的寿命的长短之间的关系.
列2×2列联表(“短寿”指寿命小于平均寿命;“长寿”指寿命大于或等于平均寿命)
|
|
短寿
|
长寿
|
合计
|
| 贪官
|
348
|
152
|
500
|
| 廉洁官员
|
93
|
497
|
590
|
| 合计
|
441
|
649
|
1090
|
由公式得K
2的观测值
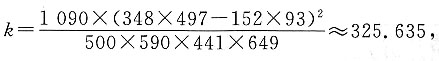
因为325.635>10.828,所以我们有99.9%的把握认为在经济上不清白与寿命短有关系.
27. 估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中,需要志愿者提供帮助的老年人的比例的估计值为
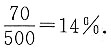
28. 能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
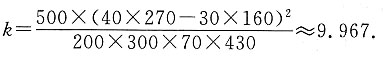
由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关.
29. 根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.
由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法抽样.
30. 关于x与y有以下数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
有两个线性模型:
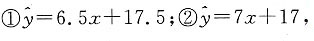
试比较哪一个模型拟合效果比较好?
由①得
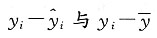
的关系如下表:
所以
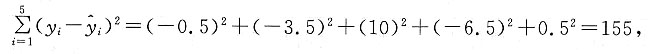
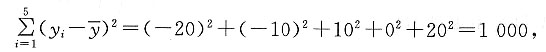
所以

由②得
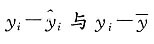
的关系如下表:
所以
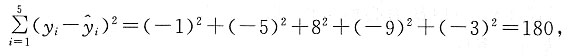
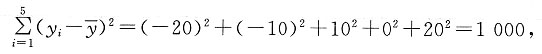
所以
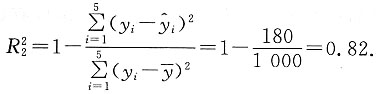
由

所以方程①的拟合效果比较好.
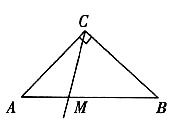
31. 如图,在等腰直角三角形ABC中,过直角顶点C在∠ACB内部任作一条射线CM,与直线AB交于点M,求AM小于AC的概率.
本题应看成射线CM在∠ACB内是等可能分布的,在AB上截取AC'=AC,则∠ACC'=67.5°,故满足条件的概率为
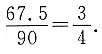
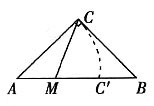
32. 在等腰直角三角形ABC中,在斜边AB上任取一点M,求AM小于AC的概率.
点M随机地落在线段AB上,故线段AB为试验的全部结果所构成的区域长度.当点M位于图中的线段AC'上(不包括点C')时,AM<AC,故线段AC'即为构成事件A的区域长度.
在AB上截取AC'=AC,于是
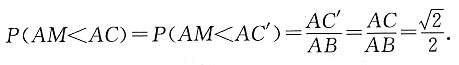
即AM小于AC的概率为
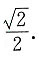
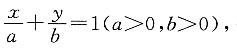 则
则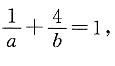 因为
因为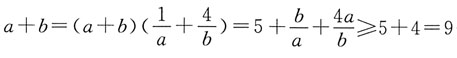 (当且仅当b=2a=6时取等号),所以直线方程为
(当且仅当b=2a=6时取等号),所以直线方程为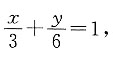 即2x+y-6=0.
即2x+y-6=0. 即(x-2)2+y2=4,则点P的轨迹是一个半径为2的圆,故面积是4π,选B.
即(x-2)2+y2=4,则点P的轨迹是一个半径为2的圆,故面积是4π,选B. ,则实数a的值为______
,则实数a的值为______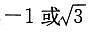
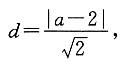 则
则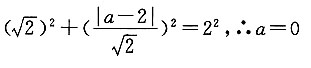 或a=4,故选D.
或a=4,故选D.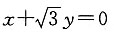 绕原点按顺时针方向旋转30°所得直线与圆x2+y2-4x+1=0的位置关系是______
绕原点按顺时针方向旋转30°所得直线与圆x2+y2-4x+1=0的位置关系是______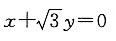 的倾斜角为150°,∴按顺时针方向旋转30°后的倾斜角为120°,
的倾斜角为150°,∴按顺时针方向旋转30°后的倾斜角为120°,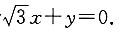 将圆的方程化为(x-2)2+y2=3,
将圆的方程化为(x-2)2+y2=3, 圆心到直线
圆心到直线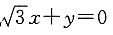 的距离为
的距离为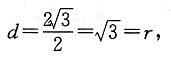
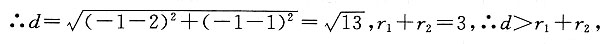
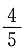
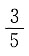
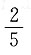
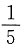
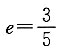 或e=-1(舍去),故选B.
或e=-1(舍去),故选B.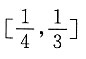
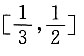
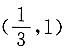
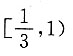
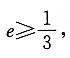 故选D.
故选D.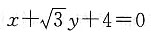 有且仅有一个交点,则椭圆的长轴长为______
有且仅有一个交点,则椭圆的长轴长为______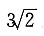

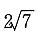
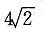
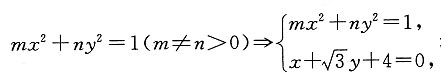 消去x得:
消去x得: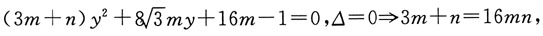 即:
即: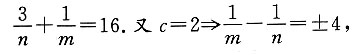 联立解得
联立解得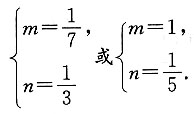 由焦点在x轴上,所以
由焦点在x轴上,所以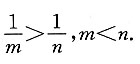 所以
所以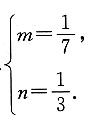 故长轴长为
故长轴长为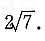
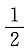
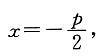 因为抛物线y2=2px(p>0)的准线与圆(x-3)2+y2=16相切,所以
因为抛物线y2=2px(p>0)的准线与圆(x-3)2+y2=16相切,所以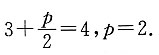
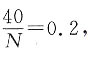 得N=200.
得N=200.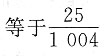
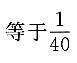


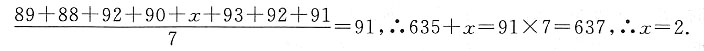
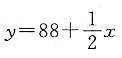



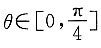 )的倾斜角的取值范围.
)的倾斜角的取值范围.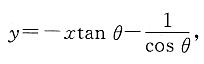 因此直线的斜率为
因此直线的斜率为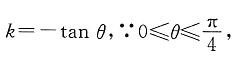
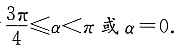
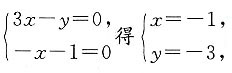 所以直线l过定点(-1,-3),因此直线总过第三象限.
所以直线l过定点(-1,-3),因此直线总过第三象限.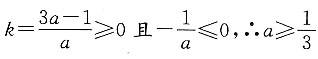 时直线l不过第二象限.
时直线l不过第二象限.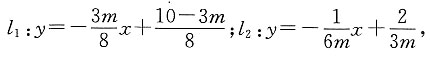 由
由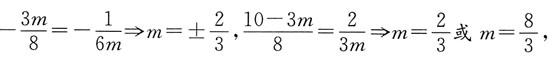 而
而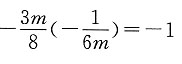 无解.
无解.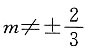 时,l1与l2相交;(2)
时,l1与l2相交;(2)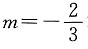 时,l1与l2平行;(3)m=0时,l1与l2垂直.
时,l1与l2平行;(3)m=0时,l1与l2垂直.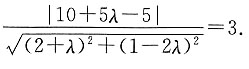 即2λ2-5λ+2=0,
即2λ2-5λ+2=0,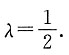 ∴l的方程为x=2或4x-3y-5=0.
∴l的方程为x=2或4x-3y-5=0.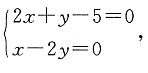 解得交点P(2,1),过P作任一直线l,设d为点A到l的距离,则d≤|PA|(当l⊥PA时等号成立).
解得交点P(2,1),过P作任一直线l,设d为点A到l的距离,则d≤|PA|(当l⊥PA时等号成立).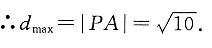
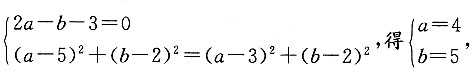
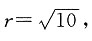 所求圆的方程为(x-4)2+(y-5)2=10.
所求圆的方程为(x-4)2+(y-5)2=10.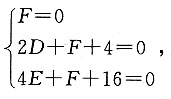 解得
解得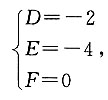 故所求圆的方程为x2+y2-2x-4y=0.
故所求圆的方程为x2+y2-2x-4y=0.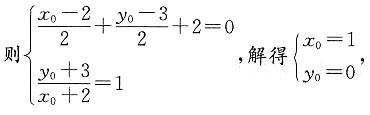 所以C'(1,0),故所求的圆方程为(x-1)2+y2=1.
所以C'(1,0),故所求的圆方程为(x-1)2+y2=1.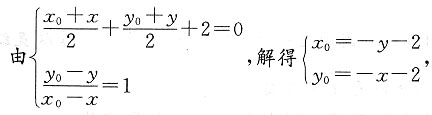 代入已知圆的方程,得(x-1)2+y2=1.
代入已知圆的方程,得(x-1)2+y2=1.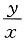 的最大值与最小值;
的最大值与最小值;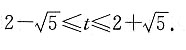
 圆的半径
圆的半径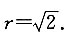
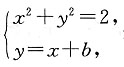 消去y得,2x2+2bx+b2-2=0,Δ=16-4b2.
消去y得,2x2+2bx+b2-2=0,Δ=16-4b2.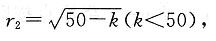
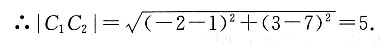
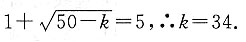
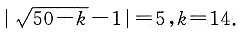
 的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为
的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为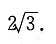
 故c=2,所以椭圆C的焦距为4.
故c=2,所以椭圆C的焦距为4.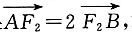 求椭圆C的方程.
求椭圆C的方程.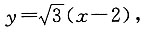 联立
联立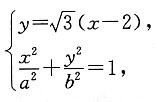
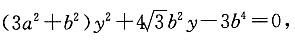 解得
解得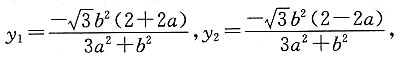
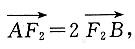 所以-y1=2y2,即
所以-y1=2y2,即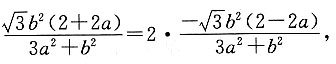
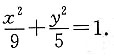
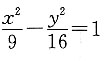 有共同的渐近线,且过点
有共同的渐近线,且过点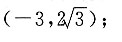
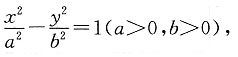
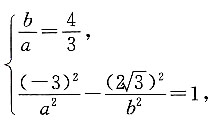 解得
解得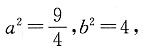 所以双曲线的方程为
所以双曲线的方程为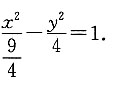
 有公共焦点,且过点
有公共焦点,且过点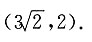
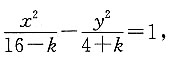 且16-k>0,4+k>0.
且16-k>0,4+k>0.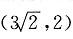 代入得k=4,且满足上面的不等式,所以双曲线方程为
代入得k=4,且满足上面的不等式,所以双曲线方程为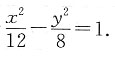
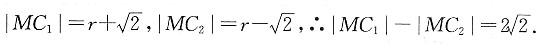
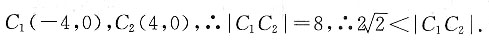
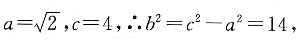 ∴点M的轨迹方程是
∴点M的轨迹方程是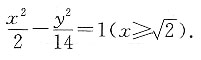
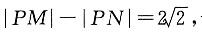 记动点P的轨迹为W.
记动点P的轨迹为W.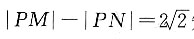 知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长
知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长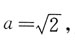 又半焦距c=2,故虚半轴长
又半焦距c=2,故虚半轴长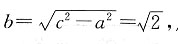 所以W的方程为
所以W的方程为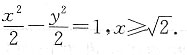
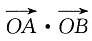 的最小值.
的最小值.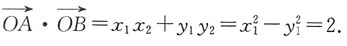 当AB与x轴不垂直时,设直线AB的方程为y=kx+m,与W的方程联立,消去y得(1-k2)x2-2kmx-m2-2=0.故
当AB与x轴不垂直时,设直线AB的方程为y=kx+m,与W的方程联立,消去y得(1-k2)x2-2kmx-m2-2=0.故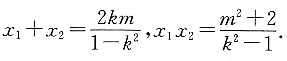 所以
所以 =x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2=
=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2=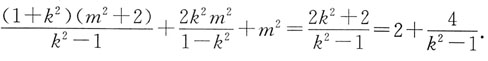
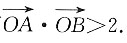 综上,当AB⊥x轴时,
综上,当AB⊥x轴时,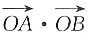 取得最小值2.
取得最小值2.
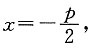 于是
于是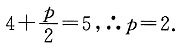

 MN所在直线的方程为
MN所在直线的方程为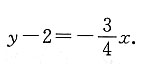

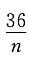 ,分层抽样的比例是
,分层抽样的比例是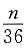 ,抽取高级教师
,抽取高级教师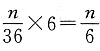 人,抽取中级教师
人,抽取中级教师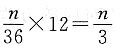 人,抽取初级教师
人,抽取初级教师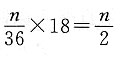 人.所以n应是6的倍数,36的约数,即n值可为6,12,18,36.
人.所以n应是6的倍数,36的约数,即n值可为6,12,18,36.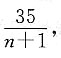 因为
因为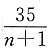 必须是整数,所以n只能取6,即样本容量n=6.
必须是整数,所以n只能取6,即样本容量n=6.
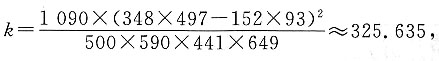 因为325.635>10.828,所以我们有99.9%的把握认为在经济上不清白与寿命短有关系.
因为325.635>10.828,所以我们有99.9%的把握认为在经济上不清白与寿命短有关系.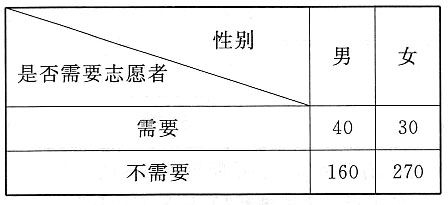
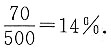
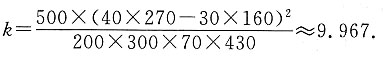
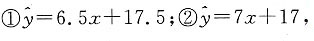 试比较哪一个模型拟合效果比较好?
试比较哪一个模型拟合效果比较好? 的关系如下表:
的关系如下表: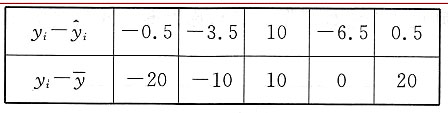
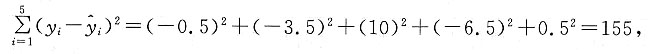
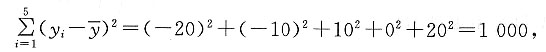

 的关系如下表:
的关系如下表: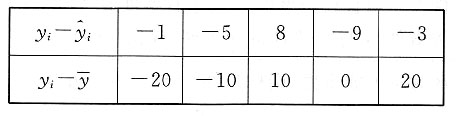
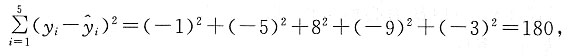
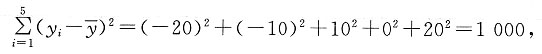
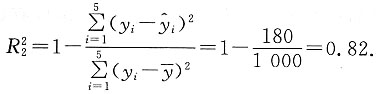
 所以方程①的拟合效果比较好.
所以方程①的拟合效果比较好.