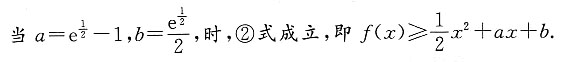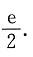银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
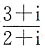 表示的复平面内的点位于______
表示的复平面内的点位于______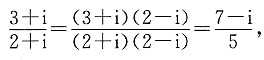 它所表示的复平面内的点是
它所表示的复平面内的点是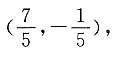 位于第四象限.
位于第四象限.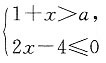 有解,则a的取值范围是______
有解,则a的取值范围是______
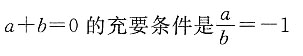
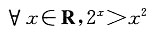

 所以A错;当x=2时,2x=x2,因此B错;a+b=0中b可取0,而
所以A错;当x=2时,2x=x2,因此B错;a+b=0中b可取0,而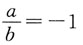 中b不可取0,因此,两者不等价,所以C错.
中b不可取0,因此,两者不等价,所以C错.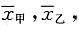 中位数分别为m甲,m乙,则______
中位数分别为m甲,m乙,则______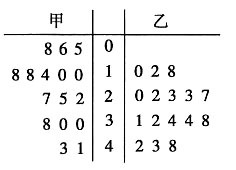
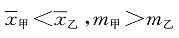
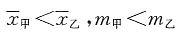
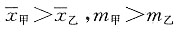
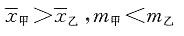

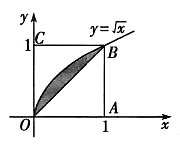
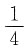
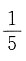
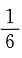
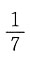
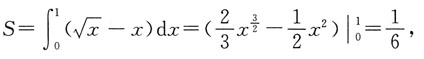 而正方形的面积为1,所以点P恰好取自阴影部分的概率为
而正方形的面积为1,所以点P恰好取自阴影部分的概率为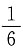 .故选C.
.故选C.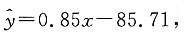 则下列结论中不正确的是______
则下列结论中不正确的是______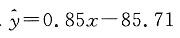 知y随x的增大而增大,所以y与x具有正的线性相关关系,故A正确;由最小二乘法建立的回归方程知回归直线过样本点的中心
知y随x的增大而增大,所以y与x具有正的线性相关关系,故A正确;由最小二乘法建立的回归方程知回归直线过样本点的中心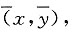 故B正确;根据回归直线方程中b的统计意义知C正确;根据回归方程预测的方法知D不正确.
故B正确;根据回归直线方程中b的统计意义知C正确;根据回归方程预测的方法知D不正确. 中,F1,F2分别是左、右焦点,P是椭圆上一点,若|PF1|=2|PF2|,则该椭圆离心率的取值范围是______
中,F1,F2分别是左、右焦点,P是椭圆上一点,若|PF1|=2|PF2|,则该椭圆离心率的取值范围是______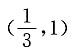

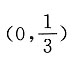
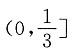
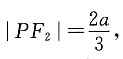 根据椭圆的几何性质,|PF2|≥a-c,故
根据椭圆的几何性质,|PF2|≥a-c,故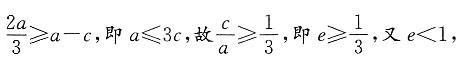 故该椭圆离心率的取值范围是
故该椭圆离心率的取值范围是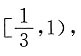 选B.
选B.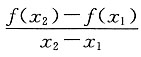 恒为正值;②f(-x)+f(x)=0;③f(x+y)=f(x)+f(y),则函数f(x)只可以是______
恒为正值;②f(-x)+f(x)=0;③f(x+y)=f(x)+f(y),则函数f(x)只可以是______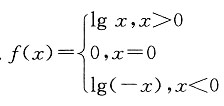
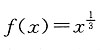
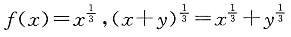 不恒成立,故选A.
不恒成立,故选A.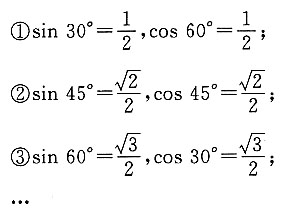
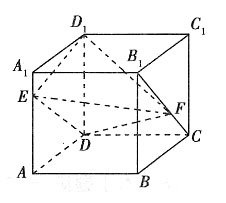
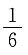
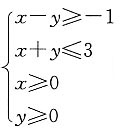 ,则z=x-2y的取值范围为______.
,则z=x-2y的取值范围为______.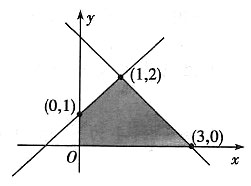
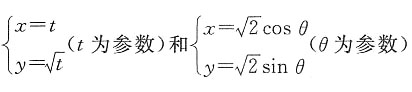 ,则曲线C1与C2的交点坐标为______.
,则曲线C1与C2的交点坐标为______.
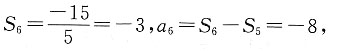
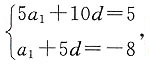 解得a1=7,所以S6=-3,a1=7.
解得a1=7,所以S6=-3,a1=7.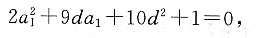
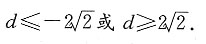
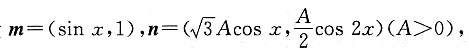 函数f(x)=m·n的最大值为6.
函数f(x)=m·n的最大值为6.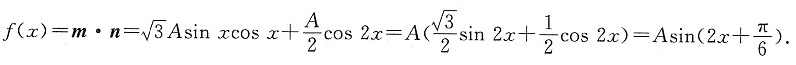
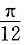 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的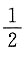 倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在
倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在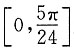 上的值域.
上的值域.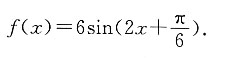
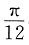 个单位后得到
个单位后得到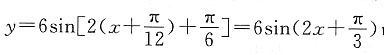 的图象;
的图象;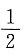 ,纵坐标不变,得到
,纵坐标不变,得到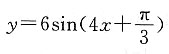 的图象.
的图象.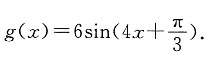
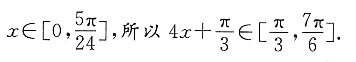
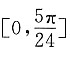 上的值域为[-3,6].
上的值域为[-3,6].| ξ | 0 | 1 | 2 | 3 | |||||||||||||||||||||
| P | 0.1 | 0.3 | 2a | a | |||||||||||||||||||||
| ξ | 0 | 1 | 2 | 3 | |||||||||||||||||||||||
| P | 0.1 | 0.3 | 0.4 | 0.2 | |||||||||||||||||||||||
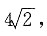 求p的值及圆F的方程;
求p的值及圆F的方程;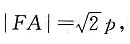 由抛物线定义可知A到l的距离
由抛物线定义可知A到l的距离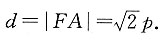
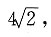 所以
所以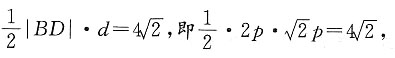
 所以∠ABD=30°,m的斜率为
所以∠ABD=30°,m的斜率为
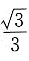 时,由已知可设
时,由已知可设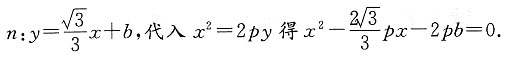
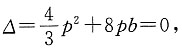 解得
解得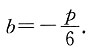
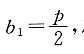 所以
所以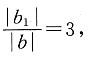 所以坐标原点到m,n距离的比值为3.
所以坐标原点到m,n距离的比值为3.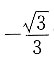 时,由图形的对称性可知,坐标原点到m,n距离的比值也为3.
时,由图形的对称性可知,坐标原点到m,n距离的比值也为3.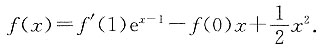
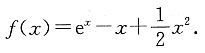
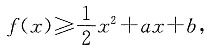 求(a+1)b的最大值.
求(a+1)b的最大值.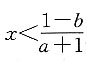 时,可得ex-(a+1)x<b,因此①式不成立.
时,可得ex-(a+1)x<b,因此①式不成立.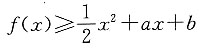 等价于b≤a+1-(a+1)ln(a+1). ②
等价于b≤a+1-(a+1)ln(a+1). ②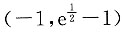 上单调增,在
上单调增,在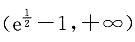 上单调递减,故h(a)在
上单调递减,故h(a)在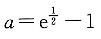 处取得最大值.从而
处取得最大值.从而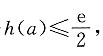 即
即