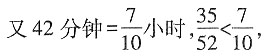一、选择题16. 下面的式子中,表示A与B互为倒数的算式是______
A.
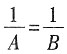
B.A÷1=B
C.B÷1=A
D.1÷B=A
A B C D
D
[解析]
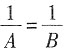
,即A=B,当A,B等于1时是互为倒数,A,B为其他数时不是互为倒数;A÷1=B,即A÷B=1,A,B的乘积不是1,故A,B不是互为倒数;B÷1=A,即B÷A=1,A,B的乘积不是1,故A,B不是互为倒数;1÷B=A,即AB=1,故A,B是互为倒数。
18. 下列说法正确的是______
A.真分数都小于1,假分数都大于1
B.在
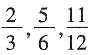
中分数单位最小的分数是
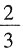
C.
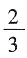
的分子加上2,分母加上3,分数的大小不变
D.一个分数的倒数都大于原数
A B C D
C
[解析] 假分数都大于等于1,A错;在
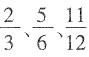
中分数单位最小的分数是
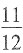
,B错;
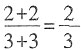
,C对;一个分数的倒数不一定都大于原数,如

的倒数是
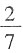
,小于
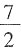
,D错。
二、填空题1. 一个分数,加上它的一个分数单位,其和是1,减去一个分数单位,约分后是
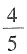
,这个分数是______。
[解析] 因为加上、减去都是一个分数单位,那么便相差两个分数单位,所以这个分数的分数单位是
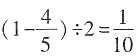
。根据“加上这个分数的分数单位,和等于1”,则原来的分数是
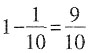
。
2. 某厂上半月完成计划的75%,下半月完成计划的50%,这个月增产______。
25%
[解析] 这个月总共完成了计划的75%+50%=125%,比单位1多125%-1=25%,因此这个月比计划增产25%。
3. 一列火车从甲地开往乙地,如果将车速提高20%,可以比原计划提前1小时到达;如果先以原速度行驶240千米后,再将速度提高25%,可提前40分钟到达,则甲乙两地距离为______,火车原来的速度为______。
540km;90km/h
[解析] 速度比为1:(1+20%)=5:6,时间比为6:5。由于车速提高20%,可比原计划提前1小时,而6比5正好多1份,因此一份是1小时,于是原速行完全程需6小时;速度比为1:(1+25%)=4:5,时间比为5:4,因此5:4=6:x,x=4.8,6-4.8=1.2小时=72分钟,甲、乙两地距离为
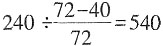
千米,火车原来的速度为540÷6=90千米/小时。
4. 甲、乙两车先后以同样的速度从A站开出,10时整,甲车距A的距离是乙车距A的距离的3倍,10时10分甲车距A的距离是乙车距A距离的2倍,甲车______时从A站开出的。
9:30
[解析] 把10点整乙车距A站的距离看作单位“1”,则10点整甲车距A站的距离是1×3=3,甲、乙两车之间的距离是3-1=2。由甲、乙两车速度相同,则甲、乙两车之间的距离一直保持是2,故10点10分乙车距A站的距离是2÷(2-1)=2,甲车距A站的距离是2×2=4,因此,10分钟时间,甲车行驶的距离是4-3=1,也就是说,10点整,甲车已经行驶了10×3=30(分钟),则有甲车是9点30分从A站出发的。
5. 41.2×8.1+11×9.25+537×0.19=______。
537.5
[解析] 原式=412×0.81+537×0.19+11×9.25=412×0.81+(412+125)×0.19+11×9.25=412×(0.81+0.19)+1.25×19+11×(1.25+8)=412+1.25×(19+11)+88=537.5。
6. 一个学生用计算器算题,在最后一步应除以10,错误的乘以10了,因此得出的错误答案为500,正确答案应是______。
5
[解析] 未乘以10之前的数为500÷10=50,故正确答案是50÷10=5。
7. 小明按一定的规律写数字:1,+2,-3,4,+5,-6,7,+8,-9,…,当他写完100个数时,他停了下来。在他所写的数中,一共有______个正数。
67
[解析] 数列中的数每三个分为一组,每组中有两个正数,一个负数,并且负数是每组中的最后一个数。由99÷3=33,33×2=66,且第100个数是正数,故小明写的这100个数中有正数66+1=67(个)。
8. 一条街上,一个骑车人与一个步行人同向而行,骑车人的速度是步行人速度的3倍,每隔10分钟有一辆公共汽车超过行人,每隔20分钟有一辆公共汽车超过骑车人。如果公共汽车从始发站每次间隔同样的时间发一辆车,那么间隔______分钟发一辆公共汽车。
8
[解析] 紧邻两辆公共汽车间的距离不变。当一辆公共汽车刚好超过步行人时,紧接着的下一辆公共汽车与步行人间的距离,就是公共汽车间隔距离。当一辆公共汽车超过行人时,下一辆公共汽车要用10分钟才能追上步行人,即追及距离=(公共汽车速度-步行速度)×10。对公共汽车超过骑车人的情形作同样的分析。由追及距离相等得到公共汽车速度等于5倍的步行速度,从而两辆公共汽车发车间隔时间等于公共汽车间隔距离除以5倍的步行速度,即10×4×步行速度÷(5×步行速度)=8(分钟)。
三、解答题计算下列各题。1.
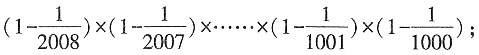
解:
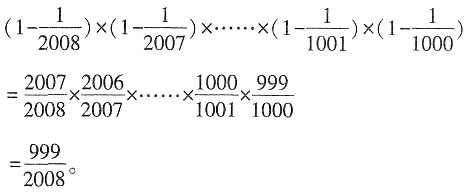
2.
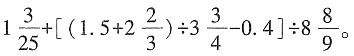
解:
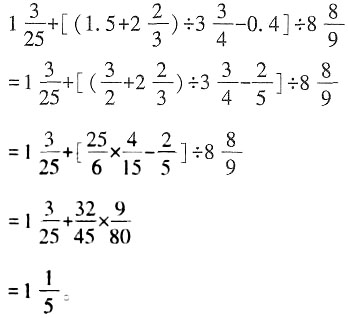
3. 一列快车和一列慢车,分别从甲、乙两地同时相对开出,快车每小时行75千米,慢车每小时行65千米,两车在距中点20千米处相遇,甲、乙两地相距多少千米?
解:相遇时,快车比慢车总共多走了2×20=40千米,
这样我们可算出到相遇时他们走的时间:40÷(75-65)=4小时,
因此,甲乙两地相距:(75+65)×4=560千米。
4. 一个圆锥形的沙堆,底面周长是12.56米,高是12分米,用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?(π取3.14)
解:12分米=1.2米,2厘米=0.02米。
沙堆的底面半径为12.56÷(2×3.14)=12.56÷6.28=2(米);
沙堆的体积为
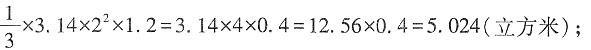
所铺沙子的长度为5.024÷(10×0.02)=5.024÷0.2=25.12(米)。
答:所铺沙子的长度为25.12米。
5. “五一”假期期间,某学校计划组织385名师生租车旅游,现知道租车公司有42座和60座两种客车,42座客车的租金每辆为320元,60座客车的租金每辆为460元。
(1)若学校只租用42座客车或者只租用60座客车,那么学校各需多少租金?
(2)若学校同时租用这两种客车共8辆(可以坐不满),而且要比单独只租用一种车辆节省租金。
请你帮助该学校选择一种最节省的租车方案。
解:(1)385÷42=9……7,故只租用42座的客车时租金为320×(9+1)=3200元;385÷60=6……25,故只租用60座的客车时租金为460×(6+1)=3220元。
(2)计算可知:
只租用1辆60座的客车时,总租金为:460×1+320×8=3020元;
当租用2辆60座的客车时,总租金为:460×2+320×7=3060元;
当租用3辆60座的客车时,总租金为:460×3+320×5=2980元;
当租用4辆60座的客车时,总租金为:460×4+320×4=3120元;
当租用5辆60座的客车时,总租金为:460×5+320×3=3260元;
当租用6辆60座的客车时,总租金为:460×6+320x1=3080元;
又由上可知租用7辆60座的客车总租金为3220元,
对比可知最节省的租车方案为:租用3辆60座的客车和5辆42座的客车,此时总租金为2980元。
答:最佳方案为租用3辆60座的客车和5辆42座的客车。
6. 购进的这批水果共有多少千克?
解:(2000+1000)÷(5-2)+100=3000÷3+100=1000+100=1100(千克)。
答:购进的这批水果共有1100千克。
7. 购进的这批水果的总金额是多少元?
解:2×1000+2000=4000(元)。
答:购进的这批水果的总金额是4000元。
8. 若小汽车送4人到达考场,然后再回到出故障处接其他人,请你通过计算说明他们能否在截止进考场的时刻前到达考场。
解:所需的时间为15×3÷60=45÷60=0.75(小时)。
又0.75小时=45分钟,45>42,
故他们不能在截止进考场的时刻前到达考场。
9. 请你设计一种运送方案,使他们能在截止进考场的时刻提前到达考场,并通过计算说明方案的可行性。
解:运送方案:让另一辆小轿车先送4名学生走,而其他4名师生同时步行前行,小桥车到达考场之后再返回途中接送其他人,设这车送4人到达后返回。
先将4人用车送到考场所需时间为15÷60=0.25(小时)。
0.25小时另4人步行的距离为0.25×5=1.25(千米),此时他们与考场的距离为15-1.25=13.75(千米)。
则用车接到4人的时间为
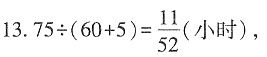
汽车由相遇点再到考场的时间也是
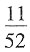
小时,
故总共用时
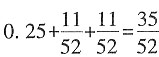
小时。
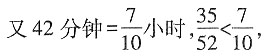
故他们能在截止进考场的时刻提前到达考场,即该方案可行。
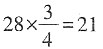 ,则差为28-21=7。
,则差为28-21=7。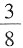 ,从另一根上截去
,从另一根上截去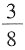 米,余下部分是______
米,余下部分是______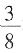 有多长,因而没法与截取
有多长,因而没法与截取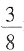 米后余下部分比较长度。
米后余下部分比较长度。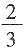 。把十位上的数字与个位上的数字调换后,新数比原数大18,则原来这个两位数个位与十位上数字的和是______
。把十位上的数字与个位上的数字调换后,新数比原数大18,则原来这个两位数个位与十位上数字的和是______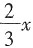 。由题意得
。由题意得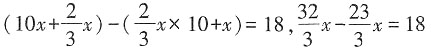 ,x=6,故十位是
,x=6,故十位是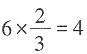 ,则原来这个两位数个位与十位上数字的和是6+4=10。
,则原来这个两位数个位与十位上数字的和是6+4=10。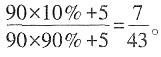
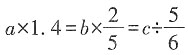 ,则a,b,c中最小的数是______
,则a,b,c中最小的数是______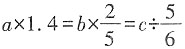 ,得
,得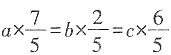 。令
。令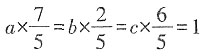 ,则
,则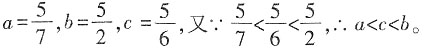
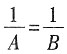
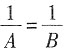 ,即A=B,当A,B等于1时是互为倒数,A,B为其他数时不是互为倒数;A÷1=B,即A÷B=1,A,B的乘积不是1,故A,B不是互为倒数;B÷1=A,即B÷A=1,A,B的乘积不是1,故A,B不是互为倒数;1÷B=A,即AB=1,故A,B是互为倒数。
,即A=B,当A,B等于1时是互为倒数,A,B为其他数时不是互为倒数;A÷1=B,即A÷B=1,A,B的乘积不是1,故A,B不是互为倒数;B÷1=A,即B÷A=1,A,B的乘积不是1,故A,B不是互为倒数;1÷B=A,即AB=1,故A,B是互为倒数。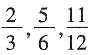 中分数单位最小的分数是
中分数单位最小的分数是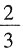
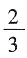 的分子加上2,分母加上3,分数的大小不变
的分子加上2,分母加上3,分数的大小不变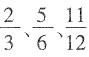 中分数单位最小的分数是
中分数单位最小的分数是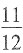 ,B错;
,B错;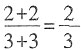 ,C对;一个分数的倒数不一定都大于原数,如
,C对;一个分数的倒数不一定都大于原数,如 的倒数是
的倒数是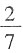 ,小于
,小于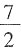 ,D错。
,D错。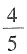 ,这个分数是______。
,这个分数是______。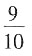
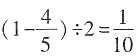 。根据“加上这个分数的分数单位,和等于1”,则原来的分数是
。根据“加上这个分数的分数单位,和等于1”,则原来的分数是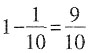 。
。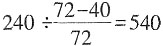 千米,火车原来的速度为540÷6=90千米/小时。
千米,火车原来的速度为540÷6=90千米/小时。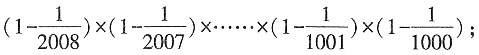
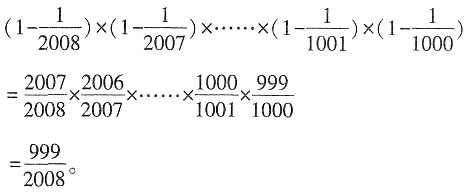
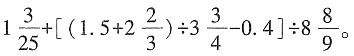
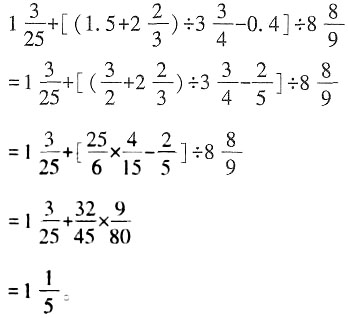
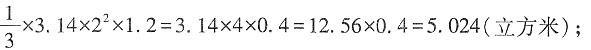
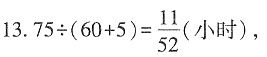
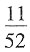 小时,
小时,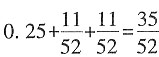 小时。
小时。