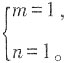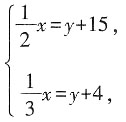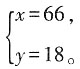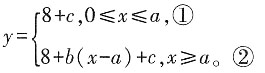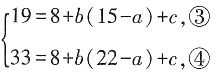一、选择题2. 已知一个直角三角形的两条直角边的长恰好是方程2x
2-8x+7=0的两个根,则这个直角三角形的斜边长是______
A.
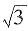
B.3
C.6
D.9
A B C D
B
[解析] 设直角三角形的两直角边的长分别为x
1和x
2,则有
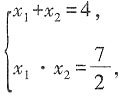
于是斜边的长为
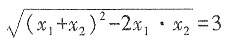
,故选B。
4. 如果|x+y-1|和2(2x+y-3)
2互为相反数,那么x,y的值为______
A.
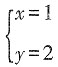
B.
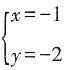
C.
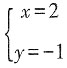
D.
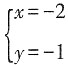
A B C D
C
[解析] 因为|x+y-1|和2(2x+y-3)
2均非负,且互为相反数,故二者均为0,从而可得方程组
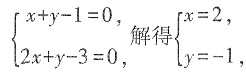
故选C。
11. 已知m,n均为非零有理数,下列结论正确的是______
A.若m≠n,则m
2≠n
2 B.若m
2=n
2,则m=n
C.若m>n>0,则
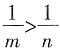
D.若m>n>0,则m
2>n
2 A B C D
D
[解析] 若m≠n,则m
2可能等于n
2,如2≠-2,2
2=(-2)
2,A错;若m
2=n
2,则m不一定等于n,如2
2=(-2)
2,2≠-2,B错;若m>n>0,则
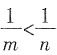
,C错;若m>n>0,则m
2>n
2,D对。
二、填空题1. 如图,点A,B在数轴上对应的实数分别为m,n,则A,B间的距离是______。(用含m,n的式子表示)
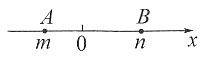
n-m
[解析] ∵n>0,m<0,∴它们之间的距离为n-m。
2.
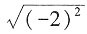
的平方根是______。
[解析]

一个正数的平方根是两个值并且这两个值互为相反数,一个正数的算数平方根是一个正数,故
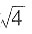
的平方根是
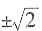
。
3. 已知方程
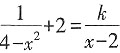
有增根,则k=______。
[解析] 方程两边都乘(2+x)(2-x),得1+2×(2+x)(2-x)=-k(2+x)。∵原方程有增根,∴最简公分母(2+x)(2-x)=0,∴增根是x=2或-2。当x=2时,
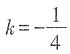
;当x=-2时,k无解。
4. 在关于x的一元二次方程(n+3)x
|n|+1+(n-1)x+3n=0中,一次项系数是______。
0或-2
[解析] ∵方程(n+3)x
|n|+1+(n-1)x+3n=0是一元二次方程,
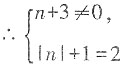
,解得n=±1。当n=1时,原方程可化为4x
2+3=0,故一次项系数是0。当n=-1时,原方程可化为2x
2-2x-3=0,故一次项系数是-2。
5. 若最简二次根式
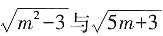
是同类二次根式,则m=______。
6
[解析] ∵最简二次根式
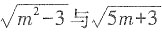
是同类二次根式,∴m
2-3=5m+3,解得m=6或m=-1。
当m=-1时,
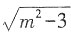
无意义,故m=6。
6. 常见的“幂的运算”有:①同底数幂的乘法;②同底数幂的除法;③幂的乘方;④积的乘方。在“(a
2·a
3)
2=(a
5)
2=a
10”的运算过程中,运用了上述幂的运算中的______。(填序号)
①③
[解析] (a2·a3)2=(a5)2(利用同底数幂的乘法得到)=a10(利用幂的乘方得到)。
7. 某市按以下规定收取每月的水费:用水量不超过6吨,按每吨1.2元收费;如果超过6吨,未超过部分仍按每吨1.2元收取,而超过部分则按每吨2元收费。如果某用户5月份水费平均为每吨1.4元,那么该用户5月份实际用水______吨。
8
[解析] ∵该用户5月份水费平均每吨1.4元,∴该用户5月份用水量超过6吨。设该用户5月份用水量为x吨。根据题意,得6×1.2+2(x-6)=1.4x,解得x=8,故该用户5月份实际用水8吨。
8. 1÷14=0.0714285714285…,那么小数点后面的第62个数字是______。
7
[解析] 1÷14=0.0714285714285…=0.0714285。从小数点后面第二位开始,它的循环周期是6,(62-1)÷6=61÷6=10……1,余数是1,故第62位就和循环节的第一位相同,即7。
三、解答题化简求值。1.
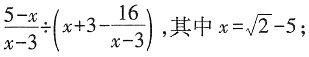
解:
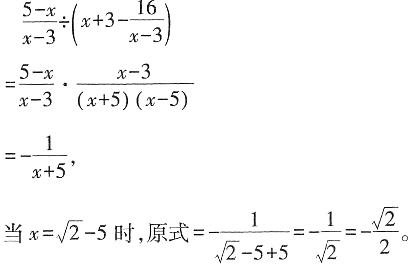
2.
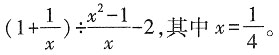
解:
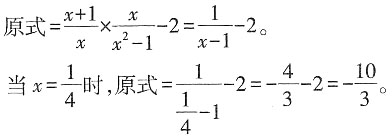
3. 若a,b互为相反数,c,d互为倒数,m是最大的负整数,求代数式

的值。
解:根据题意得a+b=0,cd=1,m=-1。
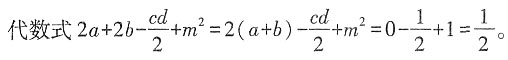
4. 果品公司购进苹果5.2万千克,每千克进价是0.98元,付运费等开支1840元,预计损耗为1%。如果希望全部进货销售后能获利17%,每千克苹果零售价应当定为多少元?
解:设每千克苹果零售价应当定为x元,
则由题可得方程5.2×104×(1-1%)x=(5.2×104×0.98+1840)×(1+17%),
解得x=1.20,即售价应为1.20元。
答:要保证获利17%,每千克苹果零售价应当定为1.20元。
5. 有理数a,b,c满足:(1)8(a-5)
2+10|c|=0;(2)-2x
2y
b+1与4x
2y
3是同类项。求:代数式2(2a
2-3ab+6b
2)-(3a
2-2009abc+9b
2-4c
68)的值。
解:由8(a-5)2+10|c|=0,得a=5,c=0。
∵-2x2yb+1与4x2y3是同类项,
∴b+1=3,
∴b=2,
∴2(2a2-3ab+6b2)-(3a2-2009abc+9b2-4c68)
=4a2-6ab+12b2-3a2+2009abc-9b2+4c68
=a2-6ab+3b2+2009abc+4c68。
当a=5,c=0,b=2时,原式=25-60+12=-23。
6. 求两人单独完成加工各需要多少天?
解:设甲单独加工完成需要x天,则乙单独加工完成需要(x-5)天,
由题意可知,
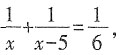
化简得x
2-17x+30=0,解得x
1=2,x
2=15,
当x=2时,x-5=-3,不符合题意,
当x=15时,x-5=10,符合题意,
因此甲单独加工完成需要15天,则乙单独加工完成需要10天。
答:甲单独加工完成需要15天,乙单独加工完成需要10天。
7. 若两人合作6天完成后,收到加工费5000元,求甲、乙两人分别可得多少钱?
解:由题可知,甲完成的工作总量为总量的
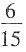
,乙完成的工作总量为总量的
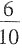
,
则
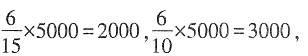
所以甲得加工费用2000元,乙得3000元。
答:甲得加工费用2000元,乙得3000元。
8. 若方程的一个根是-1,求m的值;
解:把x=-1代入关于x的二次方程m2x2+(2m+1)x+1=0,得m2-2m-1+1=0,解得m1=0,m2=2。
∵方程m2x2+(2m+1)x+1=0是一元二次方程,
∴m≠0,
∴m=2。
9. 若y=(x
1+1)(x
2+1),试求出y与m的函数关系式以及m的取值范围。
解:∵x
1,x
2是方程m
2x
2+(2m+1)x+1=0的两个实数根,
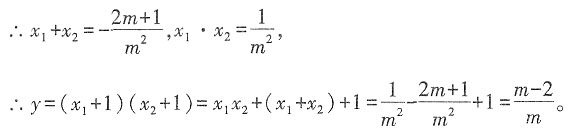
∵方程有两个实数根,
∴Δ=(2m+1)
2-4m
2=4m+1≥0,
∴m的取值范围是
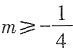
且m≠0。
A方法:剪6个侧面;B方法:剪4个侧面和5个底面。
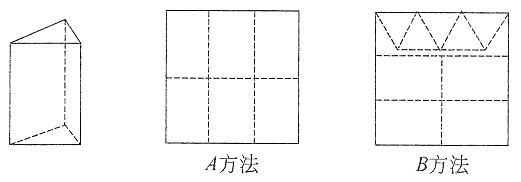
现有19张硬纸板,裁剪时x张用A方法,其余用B方法。10. 用x的代数式分别表示裁剪出的侧面和底面的个数;
解:∵裁剪时x张用A方法,
∴裁剪时(19-x)张用B方法,
∴侧面的个数为6x+4(19-x)=(2x+76)个;底面的个数为5(19-x)=(95-5x)个。
11. 若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
解:由题意,得
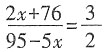
,解得x=7,故盒子的个数为
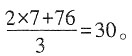
答:裁剪出的侧面和底面恰好全部用完时,能做30个盒子。
12. 解方程:
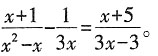
解:原方程可化为

两边同乘以3x(x-1),得x
2+3x-4=0,
故(x+4)(x-1)=0,
解得x
1=-4,x
2=1。
检验:当x=-4时,3x(x-1)≠0,所以x=-4是原方程的根;当x=1时,3x(x-1)=0,所以x=1是原方程的增根。
综上,原方程的根为x=4。
13. 已知关于x,y的方程组
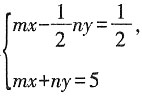
的解为
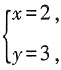
求m,n的值。
解:将
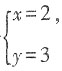
代入方程组得
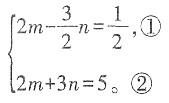
②-①得
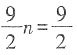
,即n=1。
将n=1代入②得m=1。
因此,
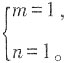
14. 某超市销售一种品牌童装,平均每天可售出30件,每件盈利40元。超市采用降价促销,若每件童装降价2元,平均每天就多售出6件。要使平均每天销售童装利润为1000元,那么每件童装应降价多少元?(列方程,并化为一般形式)
解:由题意每降价2元,平均每天多销售6件,可得降价x元时,平均每天多销售3x件,因此,降价后销售件数为(30+3x)件,每件利润为(40-x)元。
根据上面分析列方程得(30+3x)(40-x)=1000,整理得3x2-90x-200=0。
15. 用一根绳子测量井台到水面的深度,把绳子对折后垂直到水面,绳子超过井台15米,把绳子三折后垂直到水面,绳子超过井台4米。求绳子长和井台到水面的距离。
解:设绳子长为x米,静态到水面的距离为y米,
由题可得方程组
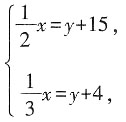
解得
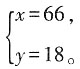
答:绳子长为66米,井台到睡眠的距离为18米。
16. 某市为了节约用水,规定:每户每月用水量不超过最低限量am
3时,只需付基本费8元和定额损耗费c元(c≤5);若用水量超过am
3时,除了付同上的基本费和损耗费外,超过部分每1m
3付b元的超额费。
| | 用水量(m3) | 应交水费(元) |
| 一月份 | 9 | 9 |
| 二月份 | 15 | 19 |
| 三月份 | 22 | 33 |
根据上表中的数据,求a,b,c。
解:设每月用水量为xm
3,支付水费为y元。
由题意知
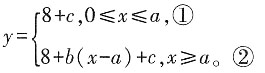
∵0<c≤5,
∴8<8+c≤13。
从表中可知,第二、三月份的水费均大于13元,故用水量15m
3,22m
3均大于最低限量am
3。
将x=15,x=22分别代入②式,得
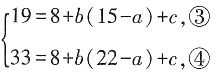
解得b=2,2a=c+19。⑤
再分析一月份的用水量是否超过最低限量。
不妨设9>a,将x=9代入②,得9=8+2(9-a)+c,即2a=c+17。⑥
⑥与⑤矛盾,故9≤a,则一月份的付款方式应选①式,故8+c=9,c=1,代入⑤式得a=10。
综上,a=10,b=2,c=1。
17. 某人驾驶一辆小轿车要作32000千米的长途旅行,除了车上装着四只轮胎,只带了一只备用胎,为了使五只轮胎磨损程度相同,司机有规律地把五只轮胎轮换使用。到达终点时,每只轮胎行驶了多少千米?
解:如果不换轮胎,则小轿车的每只轮胎都要行驶32000千米,共有四只轮胎,共行驶32000×4=128000(千米)。
现在五只轮胎轮换使用,并且要求每只磨损程度相同,即每只轮胎行驶的里程相同,因此用128000除以5即可。
故得到每只胎行驶距离为128000÷5=25600(千米)。
答:每只轮胎行驶了25600千米。
18. 若方程有实数根,求实数m的取值范围;
解:∵一元二次方程x2+2(m+1)x+m2-1=0有实数解,
∴Δ=[2(m+1)]2-4(m2-1)≥0,整理得8m+8≥0,解得m≥-1,
∴实数m的取值范围是m≥-1。
19. 若方程的两实数根分别为x
1,x
2,且满足(x
1-x
2)
2=16-x
1x
2,求实数m的值。
解:∵x1+x2=-2(m+1),x1·x2=m2-1,(x1-x2)2=16-x1x2,
∴(x1+x2)2-3x1x2-16=0,
∴[-2(m+1)]2-3(m2-1)-16=0,
∴m2+8m-9=0,解得m=-9或m=1。
∵m≥-1,
∴m=1。
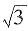
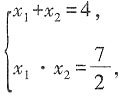 于是斜边的长为
于是斜边的长为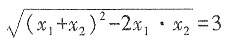 ,故选B。
,故选B。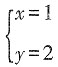
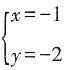
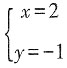
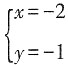
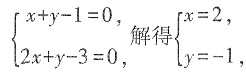 故选C。
故选C。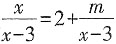 时产生增根,则m的值为______
时产生增根,则m的值为______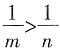
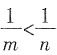 ,C错;若m>n>0,则m2>n2,D对。
,C错;若m>n>0,则m2>n2,D对。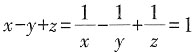 ,则______
,则______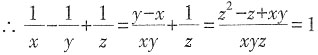 ,∴z2-z+xy=xyz,∴(z-1)(z-xy)=0,解得z=1或xy=z。当xy=z时,
,∴z2-z+xy=xyz,∴(z-1)(z-xy)=0,解得z=1或xy=z。当xy=z时,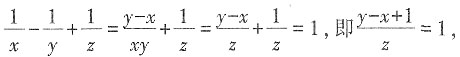 ,(y+1)(1-x)=0,解得y=-1或x=1,因此,x=1或y=-1或z=1。
,(y+1)(1-x)=0,解得y=-1或x=1,因此,x=1或y=-1或z=1。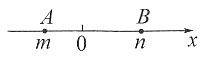
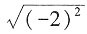 的平方根是______。
的平方根是______。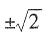
 一个正数的平方根是两个值并且这两个值互为相反数,一个正数的算数平方根是一个正数,故
一个正数的平方根是两个值并且这两个值互为相反数,一个正数的算数平方根是一个正数,故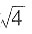 的平方根是
的平方根是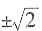 。
。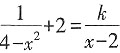 有增根,则k=______。
有增根,则k=______。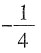
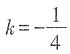 ;当x=-2时,k无解。
;当x=-2时,k无解。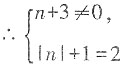 ,解得n=±1。当n=1时,原方程可化为4x2+3=0,故一次项系数是0。当n=-1时,原方程可化为2x2-2x-3=0,故一次项系数是-2。
,解得n=±1。当n=1时,原方程可化为4x2+3=0,故一次项系数是0。当n=-1时,原方程可化为2x2-2x-3=0,故一次项系数是-2。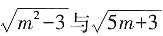 是同类二次根式,则m=______。
是同类二次根式,则m=______。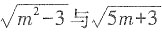 是同类二次根式,∴m2-3=5m+3,解得m=6或m=-1。
是同类二次根式,∴m2-3=5m+3,解得m=6或m=-1。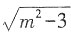 无意义,故m=6。
无意义,故m=6。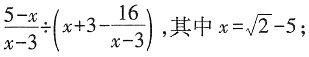
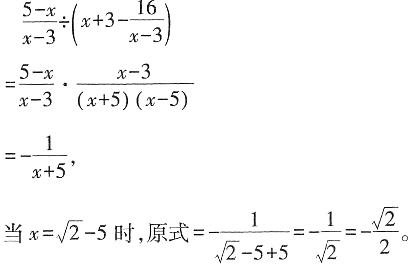
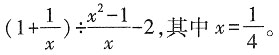
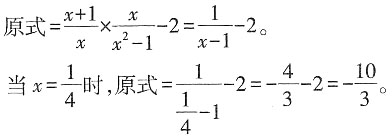
 的值。
的值。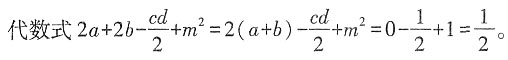
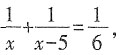
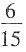 ,乙完成的工作总量为总量的
,乙完成的工作总量为总量的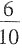 ,
,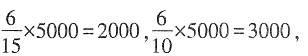
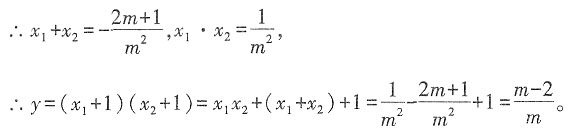
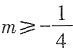 且m≠0。
且m≠0。
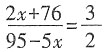 ,解得x=7,故盒子的个数为
,解得x=7,故盒子的个数为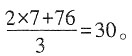
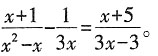

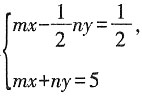 的解为
的解为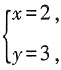 求m,n的值。
求m,n的值。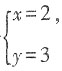 代入方程组得
代入方程组得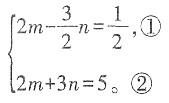
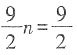 ,即n=1。
,即n=1。