一、选择题在每小题给出的四个选项中,只有一项是符合题目要求的.3. 设f(x)的一个原函数为xln(x+1),则下列等式成立的是______
A.
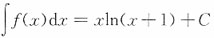
B.
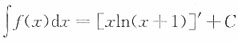
C.

D.
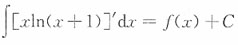
A B C D
A
[解析] 本题考查的知识点是原函数的概念.
由f(x)的一个原函数为xln(x+1),可得
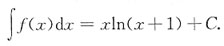
8. 设z=z(x,y)是方程
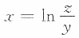
确定的隐函数,则

等于______
A B C D
C
[解析] 解法一 该函数可显化为z=ye
x,
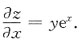
解法二 公式法
方程可化为
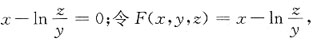
于是
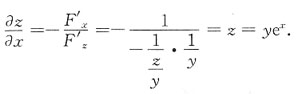
二、填空题1. 设
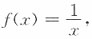
则f[f(x)]=______.
x
[解析]
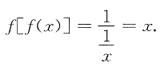
2. 从1到10这十个正整数中任取一数,取得奇数的概率为______.
[解析] 1到10这十个正整数中,1,3,5,7,9为奇数.
3. 偶函数f(x)可导,且f'(-1)=-2e,则
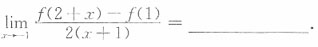
e
[解析]
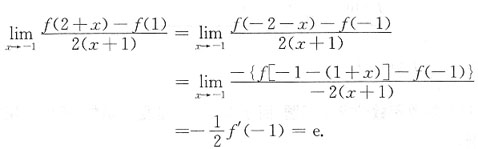
4. 当a等于______时,函数
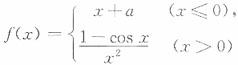
在(-∞,+∞)上连续.
[解析] 因为

要使f(x)在x=0处连续,则
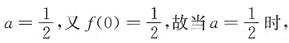
f(x)在(-∞,+∞)上连续.
5. 若
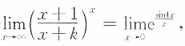
则k=______.
-3
[解析] ∵
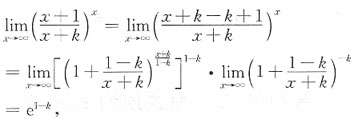
又∴
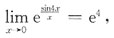
∴ e
1-k=e
4,∵ 1-k=4,k=-3.
6.
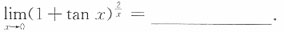
e2
[解析]
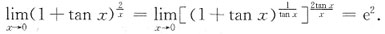
7. 函数曲线y=xe
-x的凸区间是______.
(-∞,2)
[解析] y'=(1-x)e-x,y''=(x-2)e-x<0,得x<2,即函数的凸区间是(-∞,2).
8.
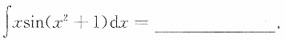
[解析] 用凑微分法积分.
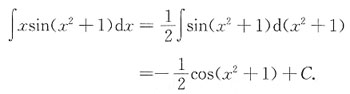
9. 设z=x
2ln(y+1),则

[解析] ∵
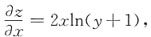
∴
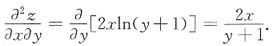
10. 设

则dz=______.
三、解答题解答应写出推理、演算步骤.1. 若
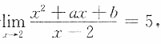
求a与b.
解 若

则当x→2时,x
2+ax+b与x-2为同阶无穷小量,
令x
2+ax+b=(x-2)(x+k), (※)
则
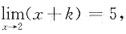
此时k=3,
代入(※)式得x
2+ax+b=(x-2)(x+3),
即x
2+ax+b=x
2+x-6,
所以a=1,b=-6.
[解析] 本题关键在于根据同阶无穷小量的定义,将x2+ax+b写成两个一次式的乘积,使得两个未知数a,b变为一个k,解答就简便了.
2. 求由方程siny+xe
y=0确定的曲线在点(0,π)处的切线方程.
解 方程两边对x求导得
cosy·y'+e
y+xe
y·y'=0,
得

所以
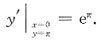
故所求切线方程为y-π=e
π(x-0),
即e
πx-y+π=0.
[解析] 本题主要考查如何求切线方程.已知切线过定点,只需求出函数在该点的导数值,即得切线的斜率,代入直线方程,进而求得切线方程.
3. 计算
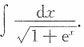
[解析] 通过换元法去根号,使被积函数有理化.注意积分后要进行反换元,即将式中的t用
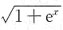
换回.
4. 求曲线
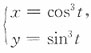
上对应于
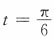
点处的法线方程.
解 注意到
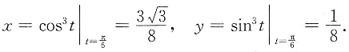
又

于是曲线上对应于
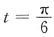
的点
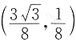
处的法线方程为
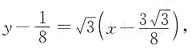
即
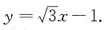
[解析] 本题中出现了以t为参变量的参数方程,求y'可以分别将y和x看作t的函数,对t求导,再求出
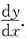
5. 计算
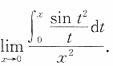
解
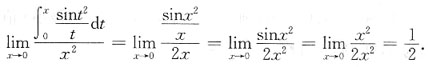
[解析] 这是变上限定积分的问题.用洛必达法则与变上限积分的导数来求解.
6. 设函数y=y(x)是由方程cos(xy)=x+y所确定的隐函数,求函数曲线y=y(x)过点(0,1)的切线方程.
解 解法一 直接求导法 等式两边对x求导得
-sin(xy)·(y+xy')=1+y',
解得
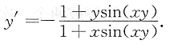
解法二 公式法 设 F(x,y)=cos(xy)-x-y.
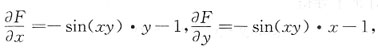
所以
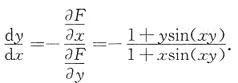
解法三 微分法 等式两边求微分得
dcos(xy)=d(x+y),
-sin(xy)(ydx+xdy)=dx+dy,
-[1+xsin(xy)]dy=[1+ysin(xy)]dx,
所以
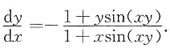
当x=0时,由方程得y=1,则
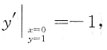
所以过点(0,1)的切线方程为
y-1=-(x-0),即x+y-1=0.
[解析] 本题是一道典型的综合题,考查的知识点是隐函数的求导计算和切线方程的求法.本题的关键是由已知方程求出y',此时的y'中通常含有x和y,因此需由原方程求出当x=0时的y值,继而得到y'的值,再写出过点(0,1)的切线方程.计算隐函数y(x)的导数,通常有三种方法:直接求导法(此时方程中的y是x的函数)、公式法(隐函数的求导公式)和微分法(等式两边求微分).
7. 求函数f(x,y)=x
2+xy+y
2-3x-6y的极值.
解 令
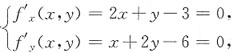
得驻点P(0,3).
在点P(0,3),
A=f''
xx(0,3)=2,B=f''
xy(0,3)=1,C=f''
yy(0,3)=2.
B
2-AC=1-4=-3<0,而A=2>0.
从而函数f(x,y)在点P(0,3)有极小值f(0,3)=-9.
[解析] 二元函数无条件极值的求解步骤为:(1)先求驻点M
i即
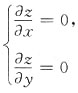
的解(x
i,y
i);
(2)求在驻点M
i处的A=f''
xx(M
i),B=f''
xy(M
i),C=f''
yy(M
i),确定B
2-AC的符号;
(3)判定:若B
2-AC<0,且A<0(A>0),则z=f(x
i,y
i)为极大(极小)值.
8. 做一个如图所示的角铁架子,其底为等腰三角形,底边长为6m,架子总长为5m,试求所用角铁为最少时,三根角铁的长度各为多少?
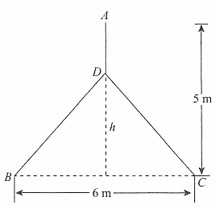
解 设等腰三角形的高为h,则
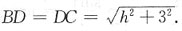
三根角铁的总长
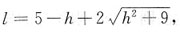
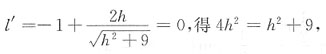
解得
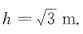
由于只有唯一的驻点,所以
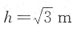
时,所用角铁为最少,此时三根角铁的长度分别为

[解析] 这是应用题中的最值问题,首先要列出函数关系式,再求其在已知条件下的最值.