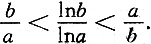一、选择题(下列每小题的选项中,只有一项是符合题意的)2. 当x→0时,与函数f(x)=x
2是等价无穷小的是______
- A.ln(1+x2)
- B.sinx
- C.tanx
- D.1-cosx
A B C D
A
[解析] 当x→0时,sinx~x,tanx~x,所以sinx,tanx是x
2的低阶无穷小;

是x
2的同阶但非等价无穷小;ln(1+x)~x,则ln(1+x
2)~x
2是x
2的等价无穷小.故选A.
4. 设
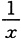
是f(x)的一个原函数,则∫x
3f(x)dx=______
A.
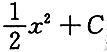
B.
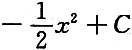
C.
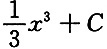
D.
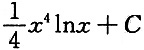
A B C D
B
[解析] 因为
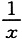
是f(x)的一个原函数,所以
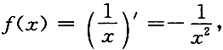
则

故选B.
5. 下列级数中收敛的是______
A.
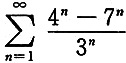
B.

C.
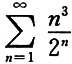
D.
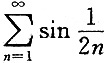
A B C D
C
[解析] 对于选项C,
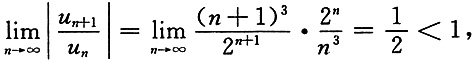
收敛,故选C.
6. 交换
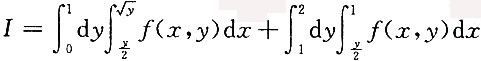
的积分次序,则下列各项正确的是______
A.

B.
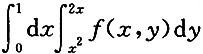
C.
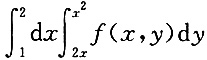
D.
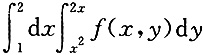
A B C D
B
[解析] 画出草图,即可得
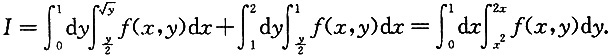
故选B.
8. 已知向量α
1=(1,2,-1,1),α
2=(2,0,k,0),α
3=(0,-4,5,-2)线性相关,则k=______
A B C D
D
[解析]
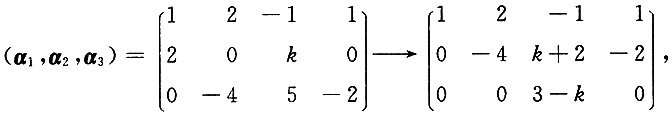
若α
1,α
2,α
3线性相关,则r(α
1,α
2,α
3)<3,即3-k=0,得k=3.故选D.
10. 有两个口袋,甲袋中有3个白球和1个黑球,乙袋中有1个白球和3个黑球,现从甲袋中任取一个球放入乙袋,再从乙袋中任取一个球,则取出白球的概率是______
A.
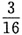
B.
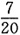
C.
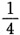
D.
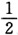
A B C D
B
[解析] 此事件分为两种情况:一种情况是从甲袋中取出的是白球,则此时从乙袋中取到白球的概率为
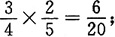
另一种情况是从甲袋中取出的是黑球,则此时从乙袋中取到白球的概率为
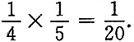
所以最终从乙袋中取到白球的概率
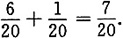
故选B.
二、填空题1. 设函数
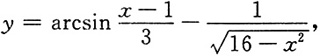
则函数的定义域为______.
[-2,4)
[解析] 联立不等式
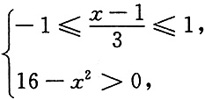
即可解得-2≤x<4.
2. 设曲线y=x
2+x-2在点M处的切线斜率为3,则点M的坐标是______.
(1,0)
[解析] 对x求导得y'=2x+1,又M处的切线斜率为3,即y'(x0)=2x0+1=3,得x0=1,代入y=x2+x-2中得y0=0,所以M的坐标为(1,0).
3. 设函数y=xarctanx,则y"=______.
[解析]
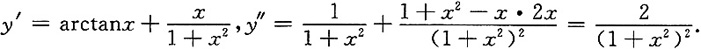
4.
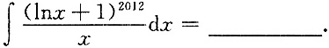
[解析]
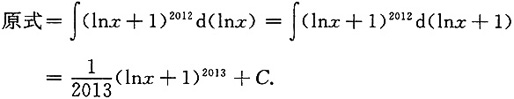
5.
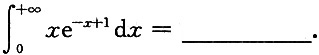
e
[解析]
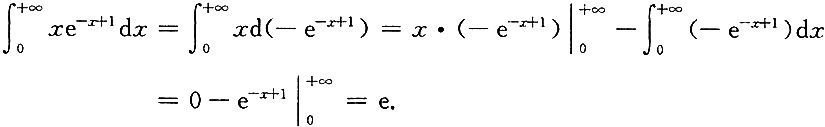
6. 幂级数
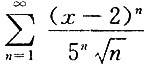
的收敛域为______.
[-3,7)
[解析] 令x-2=t,则
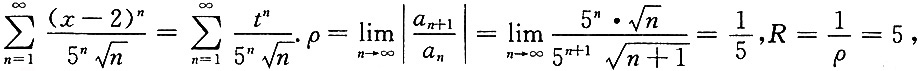
得-5<t<5,即-5<x-2<5得-3<x<7.当x=-3时,
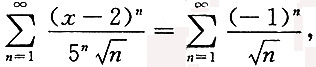
由莱布尼茨审敛法知其收敛;当x=7时,
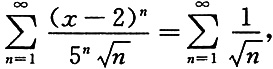
由p
-级数的敛散性知其发散,所以幂级数的收敛域为[-3,7).
7. 设A是n阶矩阵,E是n阶单位矩阵,且A
2-A-3E=O,则(A-2E)
-1=______.
A+E
[解析] A2-A-3E=O,所以A2-A-2E=E,即(A-2E)(A+E)=E,所以A-2E可逆,且(A-2E)-1=A+E.
8. 设
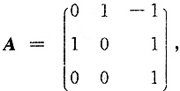
记A
-1表示A的逆矩阵,A
*表示A的伴随矩阵,则(A
-1)
*=______.
[解析] (A
-1)
*=|A
-1|A,由于|A|=-1,故|A
-1|=-1,
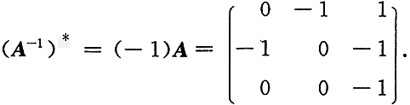
9. 设随机变量X~N(1,8),且P(X<c)=P(X≥c),则c=______.
1
[解析] P(X<c)=P(X≥c)=1-P(X<c),故
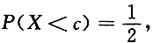
由正态分布函数的对称性知c=1.
10. 设随机变量X在区间[2,4]上服从均匀分布,则方差D(X)=______.
[解析] 由均匀分布的方差知
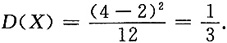
三、计算题1. 计算极限
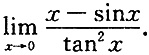
2. 求由方程y
x=xy所确定的隐函数的导数

两边取对数得xlny=lnx+lny,
两边求导得
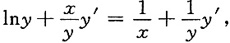
从而
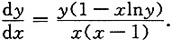
3. 计算定积分
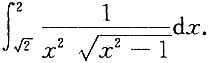
令x=sect,则dx=secttantdt,当
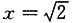
时,
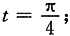
当x=2时,
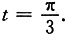
所以
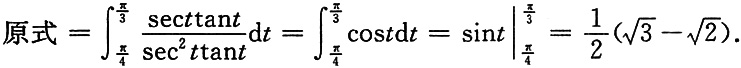
4. 求微分方程y'-2y-e
x=0的通解.
原方程可整理为y'-2y=e
x,
这是一阶线性微分方程,其中P(x)=-2,Q(x)=e
x.
所以原方程的通解为
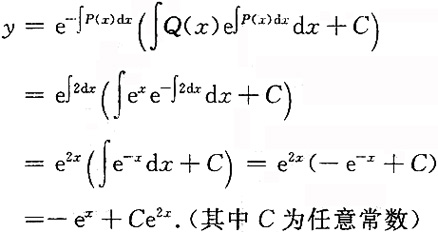
5. 计算二重积分
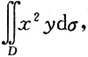
其中D是由直线x=2、y=2x和xy=2所围成的区域.
区域D如图阴影部分所示.
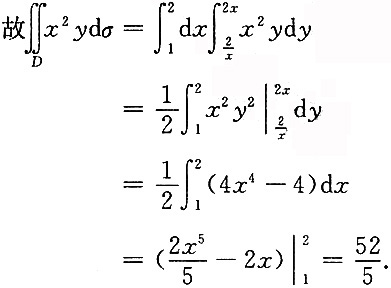
6. 设矩阵
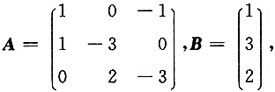
且满足AX+B=A
2B+X.求矩阵X.
由AX+B=A
2B+X可得(A-E)X=(A2-E)B=(A-E)(A+E)B,
因
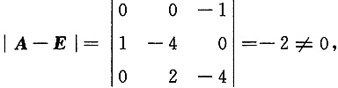
所以A-E可逆,
因此
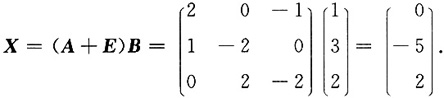
7. 设行列式
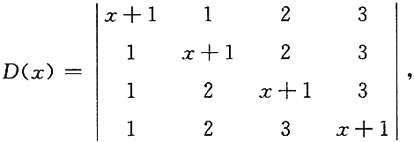
求D(x)在x=0处的导数.
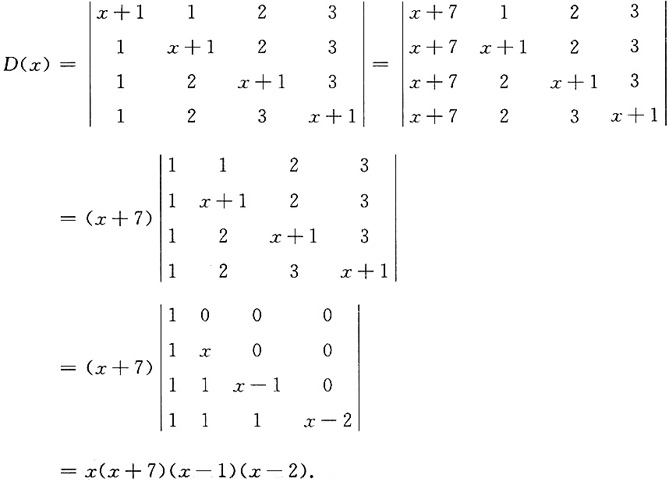
故D'(x)=(x+7)(x-1)(x-2)+x(x-1)(x-2)+x(x+7)(x-2)+x(x+7)(x-1),从而D'(0)=14.
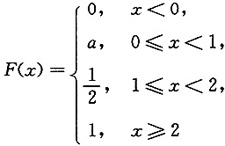 且数学期望
且数学期望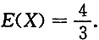
求:8. a的值;
由分布函数的性质知,随机变量X的可能取值为0、1、2,且P(X=0)=a,
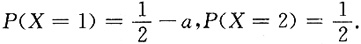
因

所以
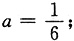
四、证明题与应用题2. 设D是由曲线y=lnx,x=e及x轴所围成的平面区域.
求:(1)平面区域D的面积S;(2)D绕y轴旋转一周所成的旋转体的体积V.
区域D如图阴影部分所示,曲线y=lnx与x轴及x=e的交点坐标分别为(1,0),(e,1).
(1)平面区域D的面积
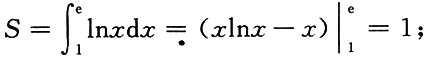
(2)D绕y轴旋转一周所成的旋转体的体积
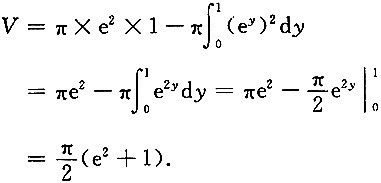
3. 证明不等式:当a>b>e时,
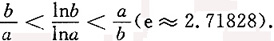
[证明] 设f(x)=xlnx,x∈(e,+∞),则f'(x)=1+lnx>0,x∈(e,+∞),所以f(x)=xlnx在x∈(e,+∞)上单调递增,从而当a>b>e时,有
f(a)>f(b)即alna>blnb即
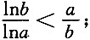
令
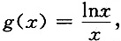
x∈(e,+∞),则
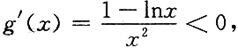
x∈(e,+∞),
所以
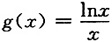
在x∈(e,+∞)上单调递减,从而当a>b>e时,有
f(a)<f(b)即

从而
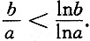
综上所述,当a>b>e时,有