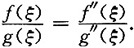银符考试题库-在线练习-安徽省专升本高等数学真题2014年

银符考试题库B12

现在是：

试卷总分：150.0

您的得分：

考试时间为：

点击“开始答卷”进行答题

安徽省专升本高等数学真题2014年

一、单项选择题
在每小题给出的四个选项中，只有一项符合题目要求．

1. 函数

的定义域为______

A.[0，3]
B.[0，2]
C.[2，3]
D.[1，3]

A B C D

B

[解析] 由

得x∈[0，2]，故选B．

2. 当x→0时，sin(x²+2x)是x的______

A.高阶无穷小
B.低阶无穷小
C.等价无穷小
D.同阶无穷小，但非等价无穷小

A B C D

D

[解析]

故选D．

3. 设f(x)为奇函数，则F(x)=f(x)(2^x+2^-x)为______

A.偶函数
B.奇函数
C.非奇非偶函数
D.无法判定奇偶性

A B C D

B

[解析] F(-x)=f(-x)(2^-x+2^x)=-f(x)(2^x+2^-x)=-F(x)，故选B．

4. 已知g(x)的一个原函数是xln(1+x²)，则∫g'(x)dx=______
A．xln(1+x²)+C
B．

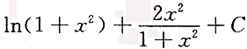
C．

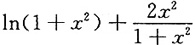
D．

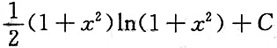
A B C D

B

[解析]

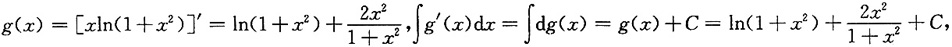
故选B．

5. 设f(x，y)为连续函数，二次积分

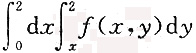
交换积分次序后为______
A．

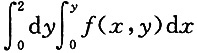
B．

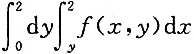
C．

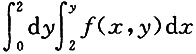
D．

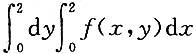
A B C D

A

[解析] 由题可知积分区域为

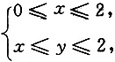
又可表示为

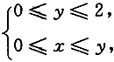
故选A．

6. 下列级数中，绝对收敛的是______
A．

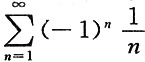
B．

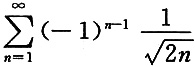
C．

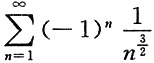
D．

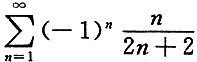
A B C D

C

[解析] 级数

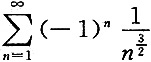
为交错级数，由莱布尼茨审敛法知其收敛；级数

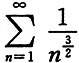
为

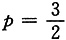
的p^-级数，收敛，故选项C为绝对收敛．选项A、B为条件收敛，选项D发散．故选C．

7. 设

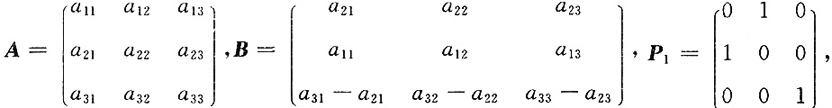
设有P₂P₁A=B，则P₂=______
A．

B．

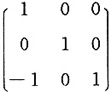
C．

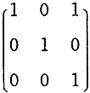
D．

A B C D

B

[解析]

由初等变换以及矩阵C、B的联系可知

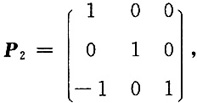
故选B．

8. 设四阶方阵A=(α，γ₂，γ₃，γ₄)，B=(β，γ₂，γ₃，γ₄)，其中α，β，γ₂，γ₃，γ₄均为四维列向量，且|A|=4，|B|=-1，则|A+2B|=______

A.9
B.18
C.24
D.54

A B C D

D

[解析] |A+2B|=|α+2β，3γ₂，3γ₃，3γ₄|=27|α，γ₂，γ₃，γ₄|+27|2β，γ₂，γ₃，γ₄|=27·4+27·2·(-1)=54，故选D．

9. 设X～N(2，σ²)，且P(0＜X＜4)=0.3，则P(X＜0)=______

A.0.3
B.0.4
C.0.35
D.0.1

A B C D

C

[解析]

故选C．

10. 设随机事件A与B相互独立，且

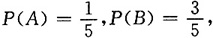
则P(A∪B)=______
A．

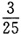
B．

C．

D．

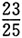
A B C D

B

[解析]

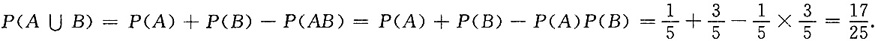
故选B．

二、填空题

1. 参数方程

确定函数y=y(x)，则

[解析]

2. 设函数

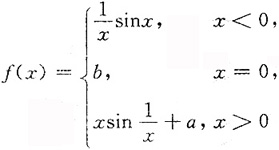
在x=0处连续，则a=______，b=______．

1，1

[解析] 由连续的定义可知，

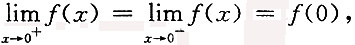
即

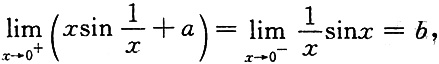
可得a=1=b．

3. 设

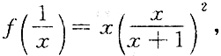
则f(x)=______．

[解析]

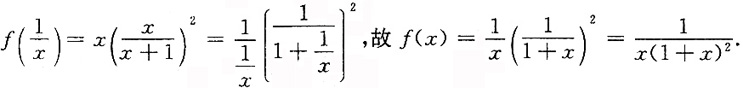
4. 设

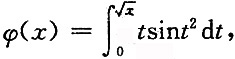
则φ'(x)=______．

[解析]

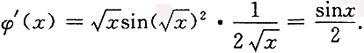
5. 设

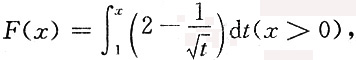
则F(x)的单调减少区间是______．

[解析]

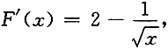
令F'(x)＜0得

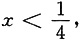
又x＞0，故单调减少区间为

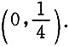
6. 幂级数

的收敛区间为______．

[解析]

故收敛半径

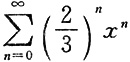
即收敛区间为

7. 设矩阵

B=A²-3A+2I，则B^-1=______．

[解析]

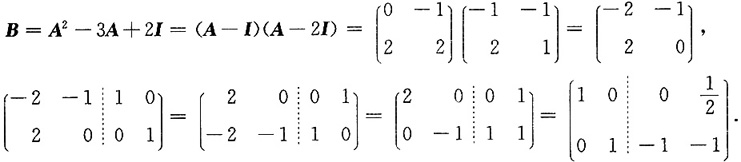
8. 设矩阵

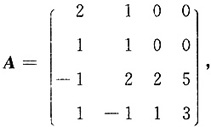
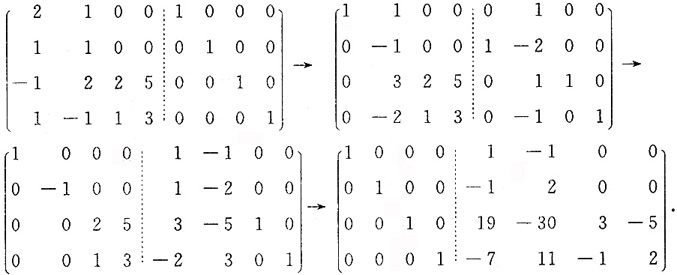
则A的逆矩阵A^-1=______．

[解析]

9. 设A、B为随机事件，P(A)=0.6，P(B|A)=0.3，则P(AB)=______．

0.18

[解析]

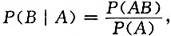
则P(AB)=0.6×0.3=0.18．

10. 从0，1，2，3，4五个数中任取三个数，则这三个数不含0的概率为______．

[解析] 任取三个数的总事件为

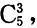
三个数不含0的事件为

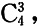
则任取三个数不含0的概率为

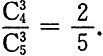
三、计算题

1. 求极限

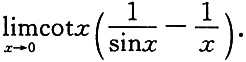
2. 设x²+y²=4，求

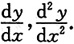
设F(x，y)=x²+y²-4，则F'_x=2x，F'_y=2y，故

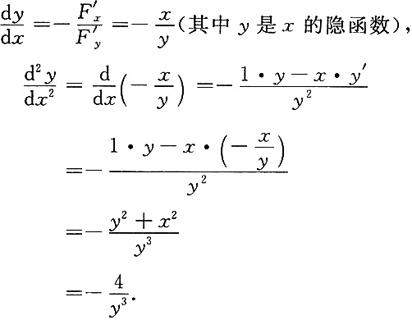
3. 计算定积分

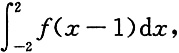
其中

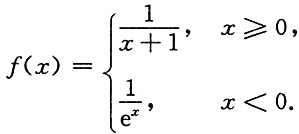
4. 求微分方程

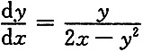
的通解．

当把x看作未知函数时，可以得到线性方程

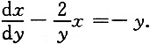
于是由一阶线性微分方程的通解公式，得原方程的通解为

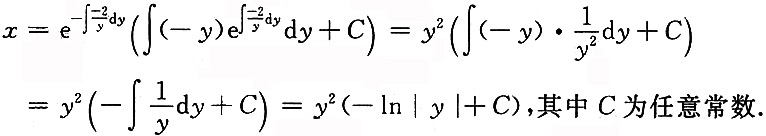
5. 求向量组α₁=(1，-1，2，4)，α₂=(0，3，1，2)，α₃=(3，0，7，14)，α₄=(1，-2，2，0)，α₅=(2，1，5，10)的一个极大线性无关组，并把其余向量用极大无关组线性表出．

所以α₁，α₂，α₄是极大线性无关组．由α₅=k₁α₁+k₂α₂+k₃α₄得方程组

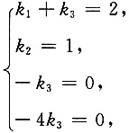
解得
k₁=2，k₂=1，k₃=0，
所以α₅=2α₁+α₂+0α₄；
由α3=k₁α₁+k₂α₂+k₃α₄得方程组

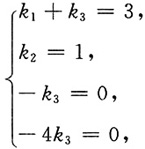
解得
k₁=3，k₂=1，k₃=0，
所以
α₃=8α₁+α₂+0α₄．

6. 解线性方程组

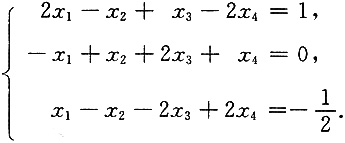
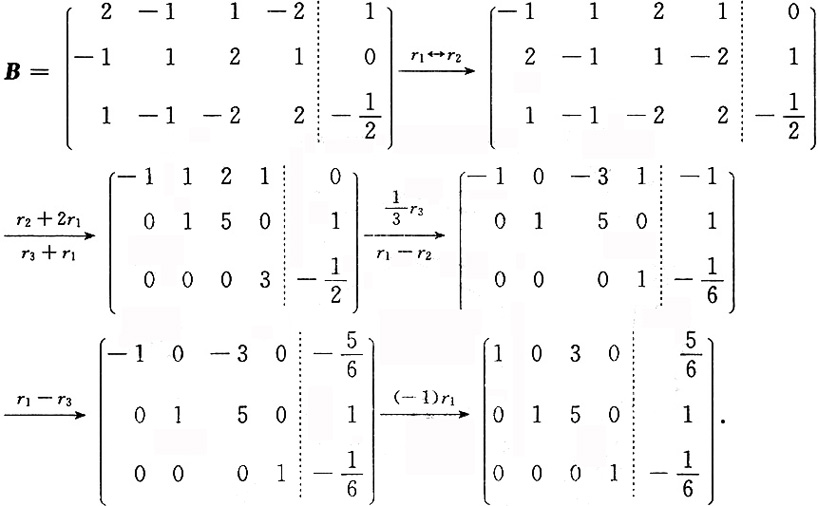
该线性方程组所对应的增广矩阵为

与原方程组同解的最简方程组为

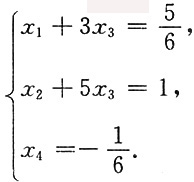
将x₃作为自由未知量，

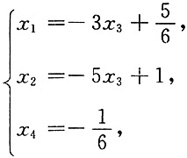
自由未知量取任意实数，写出通解

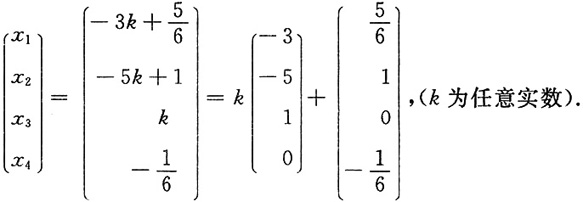
7. 计算

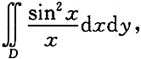
其中D是由直线y=x，2y=x及x=1围成的区域．

积分区域D如图所示．从被积函数的特点知，该积分应化为“先对y积分，后对x积分”的二次积分．

区域D可表示为：

则

X的密度函数为

求

8. P(X＞13)；

P(X＞13)=0；

9. 数学期望E(X)与方差D(X)．

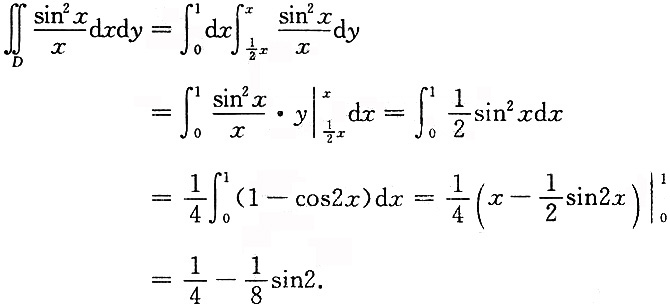
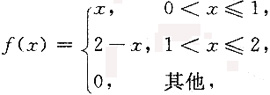
四、证明与应用题

1. 设z是由方程x-mz=φ(y-nz)所确定的关于x，y的函数，证明：z满足方程

[证明] 先求

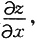
将方程x-mz=φ(y-nz)两边对x求偏导数，并注意到z是关于x，y的函数，得

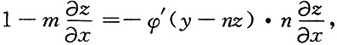
解得

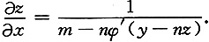
再将方程x-mz=φ(y-nz)两边对y求偏导数，得

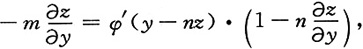
解得

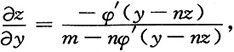
所以

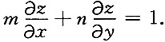
2. 过曲线y=x²(x≥0)上某点A作切线．若过点A作的切线，曲线y=x²及x轴围成的图形面积为

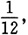
求该图形绕x轴旋转一周所得旋转体体积V．

设A点坐标为

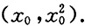
由y'=2x，得切线方程为

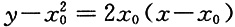
或

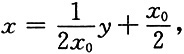
由已知

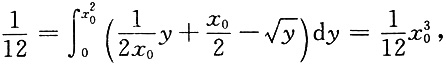
所以x₀=1，y₀=1，切线方程为2x-y-1=0，切线与x轴交点为

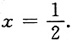
于是

设f(x)，g(x)在[a，b]上二阶可导，且g"(x)≠0，f(a)=f(b)=g(a)=g(b)=0，试证：

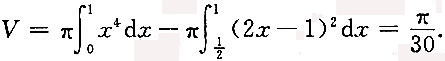
3. 在(a，b)内，g(x)≠0；

[证明] 用反证法证明：若存在x₀∈(a，b)，使g(x₀)=0，则由罗尔定理得，必存在x₁∈(a，x₀)和x₂∈(x₀，b)，使得g'(x₁)=g'(x₂)．
再由罗尔定理得，存在ξ∈(x₁，x₂)

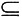
(a，b)，使得g"(ξ)=0，这与g"(x)≠0，x∈[a，b]矛盾，所以在(a，b)内g(x)≠0；

4. (a，b)内至少存在一点ξ，使得

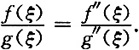
[证明] 令F(x)=f(x)g'(x)=f'(x)g(x)．由已知条件得，函数F(x)在[a，b]上满足罗尔定理的条件，故必存在ξ∈(a，b)，使得F'(ξ)=0，即
f'(ξ)g'(ξ)+f(ξ)g"(ξ)-f"(ξ)g(ξ)-f'(ξ)g'(ξ)=0，
即

一、单项选择题

1 2 3 4 5 6 7 8 9 10

二、填空题

1 2 3 4 5 6 7 8 9 10

三、计算题

1 2 3 4 5 6 7 8 9

四、证明与应用题

深色：已答题浅色：未答题