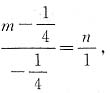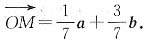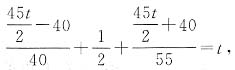二、判断题1. 艾宾浩斯遗忘曲线表明,遗忘在学习之后立即开始,而且遗忘的过程最初进展得很慢,以后逐渐加快;过了相当的时间后,几乎失去对某些事物的记忆.
对 错
B
[解析] 艾宾浩斯遗忘曲线表明,遗忘在学习之后立即开始,遗忘的过程最初进展得很快,以后逐渐缓慢;过了相当的时间后,几乎不再遗忘.
2. 需求层次理论是人本主义心理学理论在动机领域中的体现,美国心理学家巴赫是这一理论的提出者和代表人物.
对 错
B
[解析] 题干前半部分说法正确,后半句错误.需求层次理论的提出者和代表人物是美国心理学家马斯洛.
3. 课外作业是教学工作的重要反馈环节.
对 错
B
[解析] 学业成绩的考核与评定是教学工作的重要反馈环节.
4. 教学的首要任务是培养学生的道德品质和审美情趣.
对 错
B
[解析] 教学的首要任务是引导学生掌握科学文化知识和基本技能.
5. 根据知识本身的存在形式和复杂程度,知识学习可以分为下位学习、上位学习和并列结合学习.
对 错
B
[解析] 根据知识本身的存在形式和复杂程度,知识学习可以分为符号学习、概念学习和命题学习.
一、选择题2. 有长度分别为3cm、5cm、7cm、9cm的四条线段,从中任取三条线段能够组成i角形的概率是______.
A.
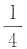
B.
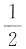
C.
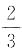
D.
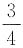
A B C D
D
[解析] 从这四条线段中任取三条线段共有四种取法,只有取3cm,5cm和9cm这三条线段不能够组成三角形,所以能够组成三角形的概率是
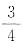
.
5. 已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1),一质点从AB的中点P
0沿与AB夹角为θ的方向射到BC上的点P
1后,依次反射到CD、DA和AB上的点P
2、P
3和P
4(入射角等于反射角),设P
4坐标为(x
4,0),若1<x
4<2,则tanθ的取值范围是______.
A.
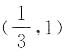
B.
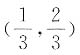
C.
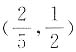
D.
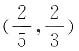
A B C D
C
[解析] 假设P
0射到BC的中点上,这样依次反射最终必会回到P
0,此时x
4=1,
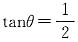
,而根据已知,1<x
4<2,所以
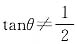
,排除A、B、D三项.因此本题选C.
二、填空题1. 0.56是由5个______和6个______组成的;也可以看作是由______个
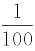
组成的.
2. 两个质数的和为18,积为65,则这两个质数是______和______.
5 13
[解析] 65=5×13,显然5与13都为质数且它们的和为18,故这两个质数为5和13.
3. 如果a=3b(a、b∈N
+),那么a和b的最大公约数是______,最小公倍数是______.
b a
[解析] 因为a=3b,所以a能被b整除,所以其最大公约数为b,最小公倍数为a.
4. 与向量a=(3,-4)平行的单位向量b=______或______.
[解析] 因为|a|=5,所以与a平行的单位向量
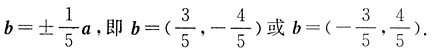
.
三、判断题1. 三角形的三条高交于一点,这点不是在三角形内就是在三角形外.
对 错
B
[解析] 对于直角三角形,它的三条高相交于一点,这一点位于三角形的直角顶点上,不在三角形内也不在三角形外.
2. 盒子里有100个白球和1个红球,任意摸出1个球,摸到红球的可能性为
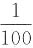
.
对 错
B
[解析] 共有101个球,故摸到红球的可能性为
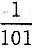
.
4. 一个正方形的边长是2分米.如果把边长增加A分米,则面积增加A
2平方分米.
对 错
B
[解析] 边长是2分米,面积=2×2=4(平方分米),边长增加A分米后,面积=(2+A)×(2+A)=A2+4A+4,面积增加(A2+4A)平方分米.
四、计算题(每小题5分,共15分)
1. 先化简,后求值:(a+b)(a-b)+b(b-2),其中
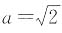
,b=-1.
解:(a+b)(a-b)+b(b-2)=a
2-b
2+b
2-2b=a
2-2b.
因为
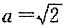
,b=-1.
所以原式
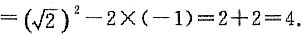
2. 计算:
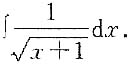
解:
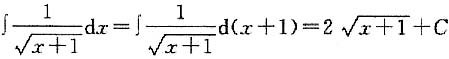
(C为常数).
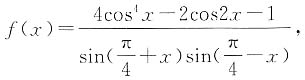
4. 当
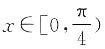
时,求函数
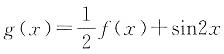
的最大值和最小值.
解:
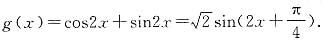
因为

,
所以
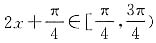
.
所以当
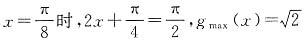
,
当x=0时,
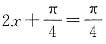
,g
min(x)=1.
五、应用题(共25分)
1. 在相距1400米的A、B两哨所,听到炮弹爆炸声的时间相差3秒,已知声速是340米/秒,炮弹爆炸点在怎样的曲线上?并求出轨迹方程.
解:设爆炸t秒后A哨所先听到爆炸声,则B哨所t+3秒后听到爆炸声,设M为爆炸点,则|MA|=340t,|MB|=340(t+3)=340t+1020.
两式相减得:|MA|-|MB|=1020,
因为|AB|=1400>1020,所以炮弹的爆炸点的轨迹是以A、B为焦点的双曲线的左半支;若爆炸后B哨所先听见爆炸声,则炮弹爆炸点的轨迹是以A、B为焦点的双曲线的右半支.
以AB为x轴,AB中点为原点建立直角坐标系(如图),
则
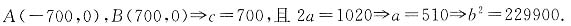
所以炮弹爆炸的轨迹方程是:
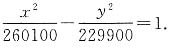
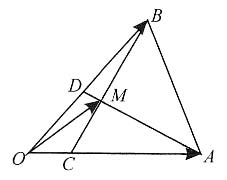
2. 如下图,在△OAB中,
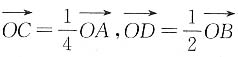
,AD与BC交于点M.设
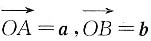
,以a、b为基底表示
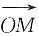
.
解:设
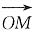
=ma+nb(m,n∈R),
则
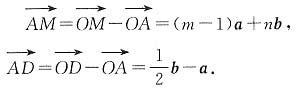
因为A、M、D三点共线,所以
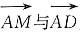
共线,所以

.即m+2n=1,
又因为
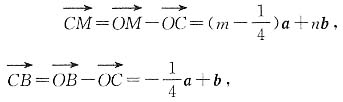
因为C、M、B三点共线,所以
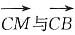
共线,
所以
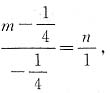
即4m+n=1,

所以
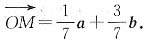
3. 某汽车从A地开往B地,如果在原计划行驶时间的前一半时间内每小时行驶40千米,后一半的时间内每小时行驶50千米则按时到达.但汽车以每小时40千米的速度从A地出发,到距离AB中点还差40千米的地方发生故障而停车半小时,以后又以每小时55千米的速度继续向前行驶,仍然按时到达B地,求A、B两地间的距离及原计划行驶的时间.
解:设原计划行驶的时间为t,则A、B两地间的距离为45t千米,于是根据题意有:
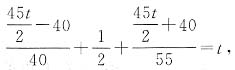
解得:t=8.
所以A、B两地间的距离为45t=45×8=360(千米).
答:A、B两地间的距离为360千米,原计划行驶的时间为8小时.
(本题也可通过建立二元一次方程组解答)
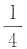
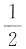
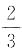
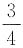
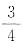 .
.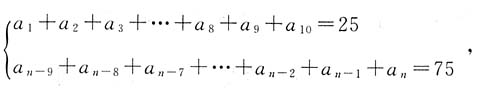 上下两式相加并根据等差数列的性质可得:a1+an=10,再由等差数列求和公式可得n=18.因此本题选C.
上下两式相加并根据等差数列的性质可得:a1+an=10,再由等差数列求和公式可得n=18.因此本题选C.
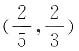
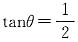 ,而根据已知,1<x4<2,所以
,而根据已知,1<x4<2,所以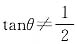 ,排除A、B、D三项.因此本题选C.
,排除A、B、D三项.因此本题选C.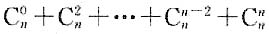 =______.
=______.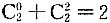 ,排除A、C两项;当n=4时,代入得
,排除A、C两项;当n=4时,代入得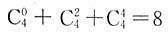 ,排除D项.因此本题选B.本题也可利用二项式定理的性质得出答案.
,排除D项.因此本题选B.本题也可利用二项式定理的性质得出答案.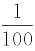 组成的.
组成的.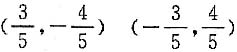
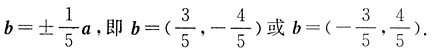 .
.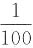 .
.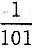 .
.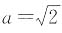 ,b=-1.
,b=-1.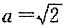 ,b=-1.
,b=-1.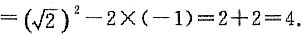
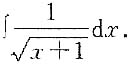
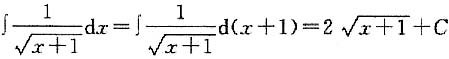 (C为常数).
(C为常数).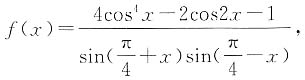
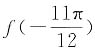 的值;
的值;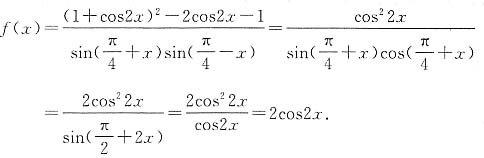
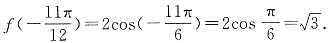
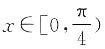 时,求函数
时,求函数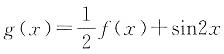 的最大值和最小值.
的最大值和最小值.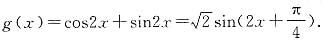
 ,
,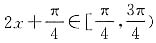 .
.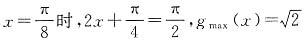 ,
,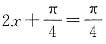 ,gmin(x)=1.
,gmin(x)=1.
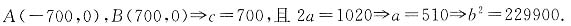
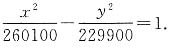
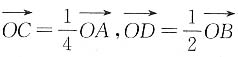 ,AD与BC交于点M.设
,AD与BC交于点M.设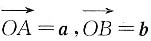 ,以a、b为基底表示
,以a、b为基底表示 .
.
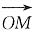 =ma+nb(m,n∈R),
=ma+nb(m,n∈R),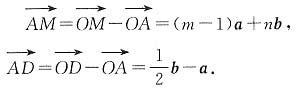
 共线,所以
共线,所以 .即m+2n=1,
.即m+2n=1,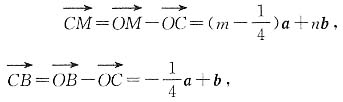
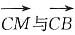 共线,
共线,