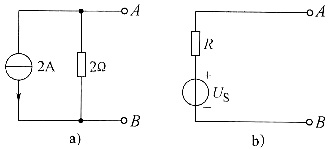
单项选择题1. 把图a所示的电路用图b所示的等效电压源代替,则等效电压源的参数为______。
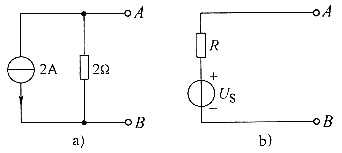
- A.US=1V,R=0.5Ω
- B.US=-1V,R=0.5Ω
- C.US=-4V,R=2Ω
- D.US=4V,R=2Ω
A B C D
C
电压源U
S的大小为RI
S=4V,方向由I
S的方向决定,故为“-”。U
S=-4V内阻R=R
S=2Ω,故选项C正确。
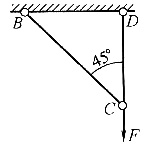
2. 已知两根杆BC、CD的抗拉刚度均为EA,则下图所示桁架C点的铅垂位移和水平位移分别为______。
A.Δx=0,
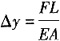
B.
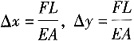
C.
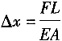
,Δy=0 D.Δx=0,Δy=0
A B C D
B
本题为简单杆系的位移计算问题。
取C点进行受力分析,知F
CD=F,F
BC=0。因此只有CD杆伸长
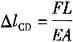
,BC杆长度不变。过C点作BC杆的垂线与CD杆伸长后的垂线交于C′点,即C点位移为
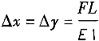
故选B。
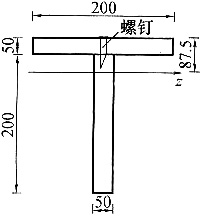
3. 一根木梁的两部分用单行螺钉连接而成,其横截面尺寸如图所示。已知横截面上的剪力F
S=3kN,惯性矩,I
z=113.5×10
-6m
4,螺钉的允许剪力为700N,则螺钉沿梁纵向的间距最大为______。
- A.52.40mm
- B.32.30mm
- C.40.20mm
- D.42.37mm
A B C D
D
本题为根据横截面上的切应力求解剪力的问题。
设钉子的间距为a。横截面上的剪力F
S引起钉子处的切应力为

,由切应力互等定律可知木梁两部分纵向连接面上的切应力τ′=τ,所以一个螺钉所承受剪力为
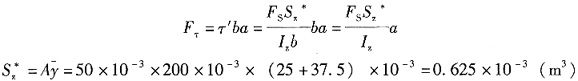
由于钉子容许剪力为700N,所以F
τ≤700,即
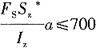
,解得:
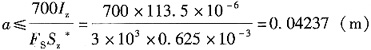
即钉子最大间距a=42.37mm,故选D。
7. 已知动点在运动的过程中恒有v=5m/s,a=10m/s
2,则动点的切向加速度a
τ和法向加速度a
n的大小为______。
- A.10m/s2,10m/s2
- B.0m/s2,10m/s2
- C.10m/s2,0m/s2
- D.0m/s2,0m/s2
A B C D
B
本题为质点运动的速度、加速度关系问题。
由于速度为常量,故a
τ=0。又
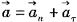
,得
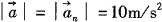
。故选B。
8. 有一直径d
n=20cm的输油管道,输油的流量Q
n=10L/s,运动粘滞系数v
n=30×10
-6m
2/s。若在模型实验中采用直径d
m=5cm的圆管,模型中分别用运动粘滞系数v
m1=1.0×10
-6m
2/s的水和v
m2=17×10
-6m
2/s的空气做实验。为保证圆管中流动相似,模型中水和空气的流量应分别为______。
- A.0.083L/s,1.42L/s
- B.0.83L/s,14.2L/s
- C.0.142L/s,0.008L/s
- D.1.42L/s,0.083L/s
A B C D
A
这是有压的粘性管流流动,要求做到原型与模型粘性力相似。就是要遵守雷诺准则,原型与模型的雷诺数相等。
计算长度比尺
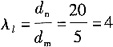
(1)水模型实验
运动粘度比尺

由雷诺准则
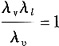
确定流速比尺
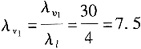
水模型实验的模型流量,由流量比尺AQ=A
2lA
V得
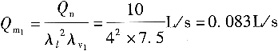
(2)空气模型实验
运动粘度比尺
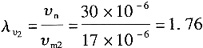
流速比尺
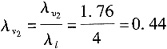
空气模拟实验的模型流量
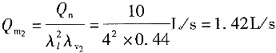
所以模型中水和空气的流量分别为0.083L/s、1.42L/s。故选项为A。
10. 一氧气瓶的容积为V,开始时充人氧气的压强为P
1,使用一段时间之后压强降为P
2,此时瓶中氧气的内能为E
2,与使用前氧气的内能E
1之比为______。
- A.E1/E2=P2/P1
- B.E1/E2=P1/P2
- C.E1/E2>P2/P1
- D.E1/E2<P1/P2
A B C D
B
设氧气为理想气体,其内能为
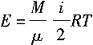
使用前的内能E
1,使用后的内能E
2,分别为
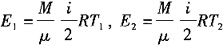
依状态方程
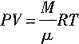
,代入E
1、E
2得:
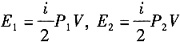
二者之比:
E
1/E
2=P
1/P
2 故正确答案为B。
11. 已知三阶方阵A的特征值为1,2,3,则|I-A
2+6A
-1|=______。
A B C D
A
本题考查特征值的性质及矩阵之间特征值的关系。
由A的特征值为1、2、3,可知,I-A
2+6A
-1的特征值为6、0、-6,所以|I-A
2+6A
-1|=0,故选A。
要知道若λ是A的特征值,则λ
2是A
2的特征值,

是A
-1的特征值。
12. 直角钢杆OAB可绕固定轴O在下图所示平面内转动,已知OA=40cm,AB=30cm,ω=2rad/s,α=1rad/s
2。则图示瞬时B点的加速度为______。
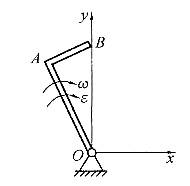
- A.223.6cm/s2
- B.200.10cm/s2
- C.206.16cm/s2
- D.200cm/s2
A B C D
C
本题为求解定轴转动刚体上质点的加速度问题。
B点的加速度为a
Bn=ω
2|OB|=4×50=200(cm/s
2),a
Bτ=α|OB|=1×50=50(cm/s
2)。该点的合加速度为
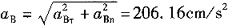
。故选C。
15. 如图所示均质等截面杆OA位于铅垂面内,杆长L,重P,与水平夹角θ=60°。根据动静法计算AB绳突然剪断瞬时OA杆的角加速度为______。
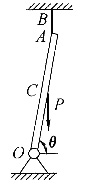
A.
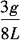
(顺时针) B.
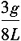
(逆时针) C.
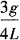
(顺时针) D.
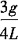
(逆时针)
A B C D
C
本题为动静法的应用问题。
绳子剪断瞬时,OA杆绕O点转动,杆上惯性力包括:
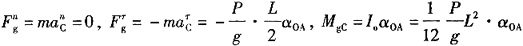
由平衡方程∑M
A=0,有:
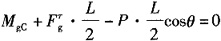
解得
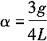
(顺时针)。故选C。
17. 在双缝实验中,双缝与屏之间的距离D=1.5m,照射双缝的单色光波长λ=5.5×10
-7m,测得中央明条纹两侧的两个第五级明条纹之间的距离为15.0×10
-3m,则两缝之间的距离为______。
- A.1.35×10-3m
- B.0.55×10-3m
- C.1.50×10-3m
- D.2.0×10-3m
A B C D
B
双缝干涉的明暗条纹之间的间距是相等的。相邻两条纹之间的间距均为
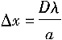
依题意:两个第五级明条纹之间的间距为10Δx=15×10
-3m,所以Δx=1.5×10
-3m,代入上式得:
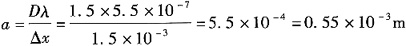
即两缝之间的间距为0.55mm。故正确答案为B。
19. 如图所示结构,已知L=4m,q=6kN/m,M=8kN·m,则A处的约束反力偶为______。
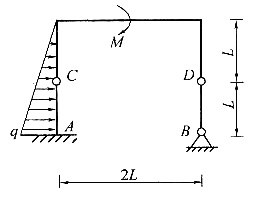
- A.14kN·m
- B.28kN·m
- C.44kN·m
- D.56kN·m
A B C D
D
本题为求解支座反力偶的问题。
取CD杆研究,由∑M
C=0,解得R
B=2kN。
取整体分析,由
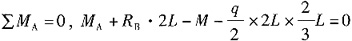
,解得M
A=56kN·m
故选D。
20. 平面区域D:x
2+y
2≤9,则
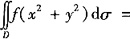
______。
A.
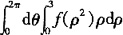
B.
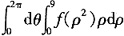
C.
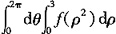
D.
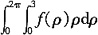
A B C D
A
考查利用极坐标计算二重积分。
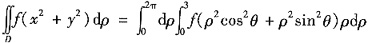
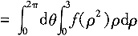
,故选A。
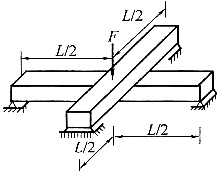
22. 如图所示,1、2两梁相互垂直并在中点相互接触,设两梁材料及长度均相同,而截面的主惯性矩分别为I
1和I
2,则1、2两梁承受的荷载之比为______。
A.
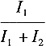
B.
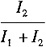
C.
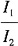
D.
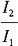
A B C D
C
本题为梁的简单超静定问题。
因为两个梁中点相互接触,则两根梁中点挠度相等,即v
1=v
2。
带入
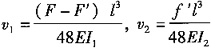
,解得
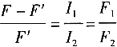
故选C。
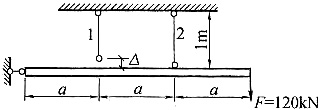
25. 如图所示结构的刚梁吊在两根钢杆上,若1杆长度短Δ=0.1mm,两杆材料弹性模量均为E=200GPa,横截面积分别为A
1=2000mm
2,A
2=1000mm
2。则装配后并在荷载F作用下两杆横截面上的应力为______。
- A.70.3MPa,106.7MPa
- B.73.3MPa,106.7MPa
- C.73.3MPa,100.7MPa
- D.70.3MPa,100.7MPa
A B C D
B
本题为拉压杆一次超静定问题。
由变形协调知2(Δl
1-Δ)=Δl
2,带入物理关系
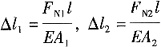
,得:
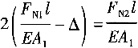
(1)
由静力学平衡方程
∑M(A)=F
N1·a+F
N2·2a-F·3a=0 (2)
联立方程(1)、(2),解得
F
N1=146.6kN F
N2=106.7kN
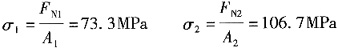
故选B。
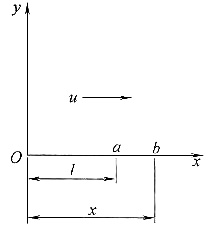
26. 一平面谐波,在空间以速度u沿x轴的正方向传播,如图所示,在波线上距原点为l的a点的振动方程为
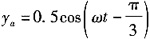
则该平面谐波的波动方程为______。
A.
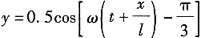
B.
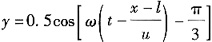
C.
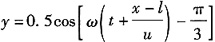
D.
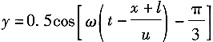
A B C D
B
在a点的振动方
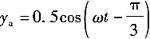
中,振动位相为
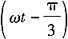
,而波动是振动位相的传播。如题图所示,设b点为x轴上任意一点,该点的振动位相滞后于a点,其滞后的时间为的
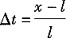
,可得b点的振动位相为
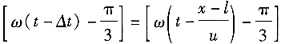
所以b点的振动方程为
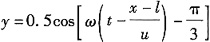
由于b点是平面谐波传播方向上的任意一点,故上式为该平面谐波的波动方程。正确答案是B。
27. N件产品中有M件次品,从中任取n件,则n件产品中恰有k件次品的概率为______。
A.

B.
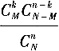
C.
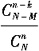
D.
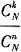
A B C D
B
从N件中取n件共有C
nN种取法,这n件产品中恰有k件次品,则有C
kMC
n-kN-M种取法。所以所求的概率为
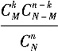
。
32. 已知如图所示T形截面梁上的弯矩M=3.1kN·m,截面对z轴的惯性矩I
z=53.1×10
-6m
4,则中性轴以上部分截面的正应力构成的总压力为______。
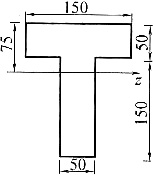
- A.-22.8kN
- B.22.8kN
- C.-12.8kN
- D.12.8kN
A B C D
A
本题为根据截面上的正应力求解法向内力的问题。
根据
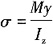
,得:
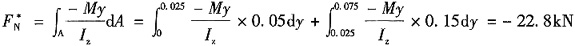
故选A。
34. 已知
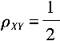
,E(X)=E(Y)=0,E(X
2)=E(Y
2)=4,则D(X+Y)=______。
A B C D
B
本题考查协方差,相关系数的关系。
D(X)=E(X
2)-E(Y)=4,同理D(Y)=4,
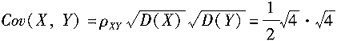
=2
所以D(X+Y)=D(X)+D(Y)+2Cov(X,Y)=4+4+2×2=12。故选B。



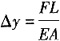 B.
B.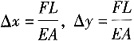
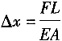 ,Δy=0 D.Δx=0,Δy=0
,Δy=0 D.Δx=0,Δy=0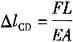 ,BC杆长度不变。过C点作BC杆的垂线与CD杆伸长后的垂线交于C′点,即C点位移为
,BC杆长度不变。过C点作BC杆的垂线与CD杆伸长后的垂线交于C′点,即C点位移为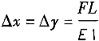

 ,由切应力互等定律可知木梁两部分纵向连接面上的切应力τ′=τ,所以一个螺钉所承受剪力为
,由切应力互等定律可知木梁两部分纵向连接面上的切应力τ′=τ,所以一个螺钉所承受剪力为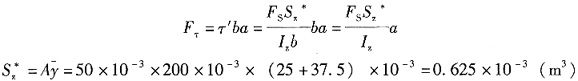
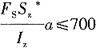 ,解得:
,解得: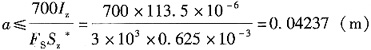
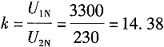
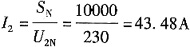
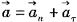 ,得
,得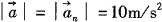 。故选B。
。故选B。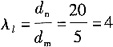

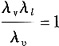 确定流速比尺
确定流速比尺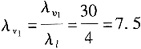
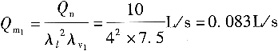
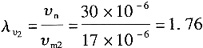
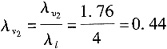
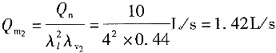
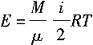
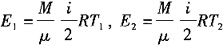
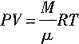 ,代入E1、E2得:
,代入E1、E2得: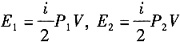
 是A-1的特征值。
是A-1的特征值。
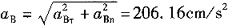 。故选C。
。故选C。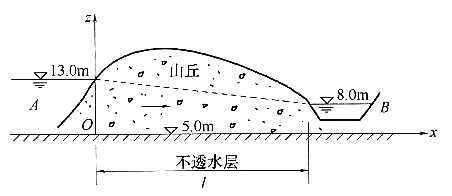
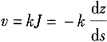 导出单宽渗流量q的计算式
导出单宽渗流量q的计算式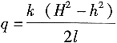
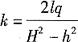
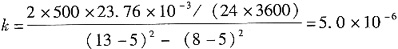

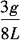 (顺时针) B.
(顺时针) B.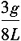 (逆时针) C.
(逆时针) C.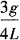 (顺时针) D.
(顺时针) D.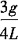 (逆时针)
(逆时针)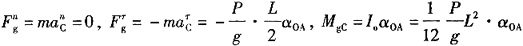
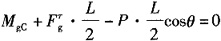
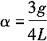 (顺时针)。故选C。
(顺时针)。故选C。
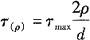 ,则阴影部分的扭矩为
,则阴影部分的扭矩为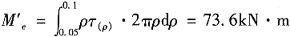
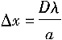
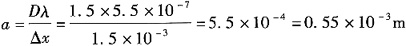
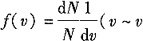 +dv),则
+dv),则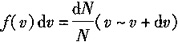 。此式表示的物理意义是:分子速率在v~v+dv区间的分子数占总分子数的百分比。故正确答案为C。
。此式表示的物理意义是:分子速率在v~v+dv区间的分子数占总分子数的百分比。故正确答案为C。
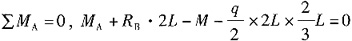 ,解得MA=56kN·m
,解得MA=56kN·m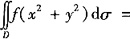 ______。
______。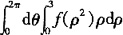 B.
B.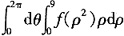
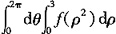 D.
D.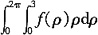
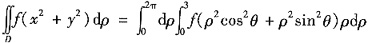
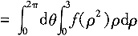 ,故选A。
,故选A。
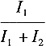 B.
B.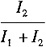 C.
C.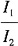 D.
D.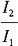
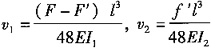 ,解得
,解得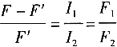

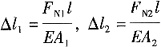 ,得:
,得: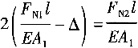 (1)
(1)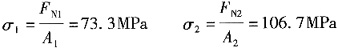
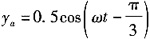

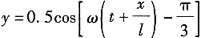 B.
B.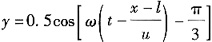
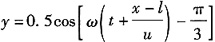 D.
D.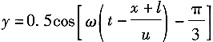
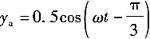 中,振动位相为
中,振动位相为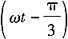 ,而波动是振动位相的传播。如题图所示,设b点为x轴上任意一点,该点的振动位相滞后于a点,其滞后的时间为的
,而波动是振动位相的传播。如题图所示,设b点为x轴上任意一点,该点的振动位相滞后于a点,其滞后的时间为的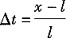 ,可得b点的振动位相为
,可得b点的振动位相为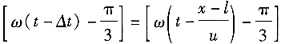
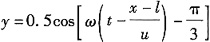
 B.
B.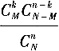 C.
C.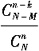 D.
D.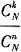
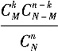 。
。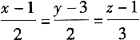 垂直的平面方程为______。
垂直的平面方程为______。
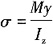 ,得:
,得: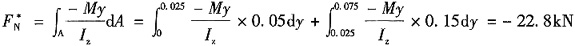
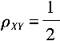 ,E(X)=E(Y)=0,E(X2)=E(Y2)=4,则D(X+Y)=______。
,E(X)=E(Y)=0,E(X2)=E(Y2)=4,则D(X+Y)=______。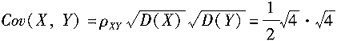 =2
=2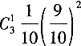 B.
B.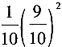 C.
C.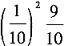 D.
D.
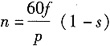 ,随着频率提高,转速上升,故选项A正确。
,随着频率提高,转速上升,故选项A正确。