一、选择题8. 二元函数z=x
3-y
3+3x
2+3y
2-9x的极小值点为______
- A.(1,0)
- B.(1,2)
- C.(-3,0)
- D.(-3,2)
A B C D
A
[考点] 本题考查了二元函数的极值的知识点.
[解析] 因z=x
3-y
3+3x
2+3y
2-9x,于是
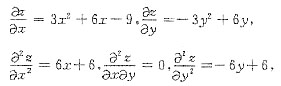
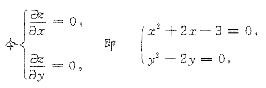
得驻点(-3,0),(-3,2),(1,0),(1,2).
对于点(-3,0),A=-18+6=-12,B=0,C=6,B
2-AC=72>0,故此点为非极值.
10. 方程x
2+2y
2+3z
2=1表示的二次曲面是______.
A B C D
D
[考点] 本题考查了二次曲面的知识点.
[解析] 可将原方程化为

,所以原方程表示的是椭球面.
15. 设∫f(x)dx=e
x+C,则∫xf(1-x
2)dx为______
A.
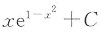
B.
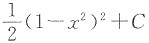
C.
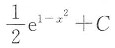
D.
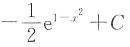
A B C D
D
[解析] 本题考查了换元积分法求不定积分的知识点.
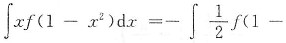
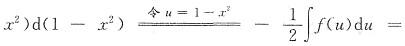

.
另解:将∫f(x)dx=e
x+C两边对x求导得f(x)=e
x,则
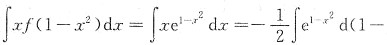
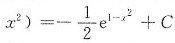
.
20. 下列级数中发散的是______
A.

B.
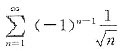
C.
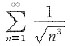
D.
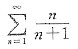
A B C D
D
[考点] 本题考察了级数的敛散性的知识点.
[解析] 当n>5时,2
n>n
2,所以
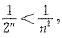
故选项A收敛;
选项B是交错级数,
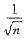
单调递减且
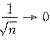
(n→∞),故选项B收敛;
选项C,
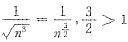
,所以选项C收敛;
用排除法故知选项D正确,其实从收敛的必要条件
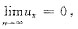
而
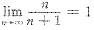
,故选项D发散.
22.
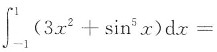
A B C D
D
[解析] 本题考查了定积分的奇偶性的知识点.
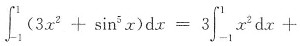
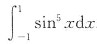
.因为f
1(x)=x
2为偶函数,所以
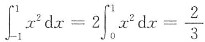
.因为f
2(x)=sin
5x为奇函数,所以
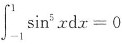
.故
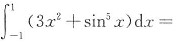
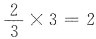
.
28. 设y=lnx,则y"______
A.
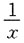
B.
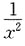
C.
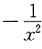
D.
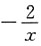
A B C D
C
[解析] y=lnx,
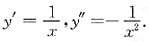
故选C.
29. 平面π:x+2y-z+3=0与直线l:
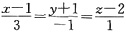
的位置关系是______
- A.互相垂直
- B.互相平行但直线不在平面上
- C.即不平行也不垂直
- D.直线在平面上
A B C D
D
[解析] 平面π的法向量n={1,2,-1},直线l的方向向量s={3,-1,1},因为
1×3+2×(-1)-1×1=0
n⊥s,即直线l与平面π平行.
又直线l上取点M
0(1,-1,2)代入平面π的方程,有1+2×(1)-2+3=0,即点M
0在平面π上,则直线l在平面π上.(答案为D)
30.
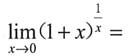
______.
A.0
B.1
C.
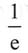
D.e
A B C D
D
[解析] 由重要极限公式可知
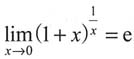
,所以选D.
二、填空题1. 设区域D为y=x
2,x=y
2围成的在第一象限内的区域,则
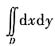
=______.
[解析] 本题考查的知识点为二重积分的计算.

2. 过坐标原点且与直线
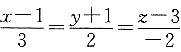
垂直的平面方程为______.
3. 直线l过点(0,2,-1)且与平面4x-y+2z-8=0垂直,则直线l的方程为______.
4. 设
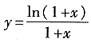
,则y'|
x=0=______.
1
[解析] 本题考查的知识点为导数的计算.
由于
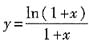
,可知
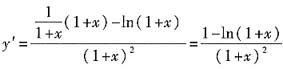
,进而有y'|
x=0=1.
5. 幂级数
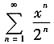
的收敛区间为______.
(-2,2)
[解析] 本题考查的知识点为幂级数的收敛区间.
由于所给级数为不缺项情形,
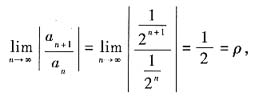
可知收敛半径
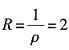
,收敛区间为(-2,2).
6. 曲线
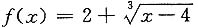
的拐点是______.
7. 设f(2x)=ln x,则f'(x)=______.
[解析] 令t=2x,可知
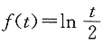
=ln t-1n 2,从而f(x)=ln x-ln 2,
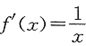
.
8. 级数
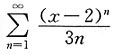
的收敛区间为______.(不包括端点)
(1,3)
[解析] 级数
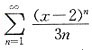
的一般项
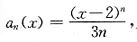
则由比值法有:
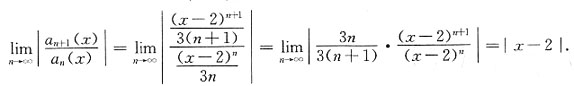
即当|x-2|<1时收敛,所以有-1<x-2<1,即1<x<3.
故收敛区间为(1,3).
9. 设
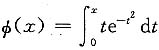
,则当x=______时,

取极______值.
0,小
[解析] 令
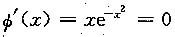
,则x=0为
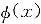
的驻点.

,故当x=0时,
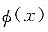
取极小值.
10. 设y=cos(e
-x),则y'(0)=______.
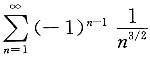 是______
是______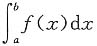
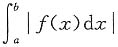
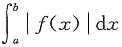
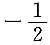
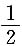
 ,由此知该方程表示的是准线为圆、母线平行于y轴的圆柱面.
,由此知该方程表示的是准线为圆、母线平行于y轴的圆柱面.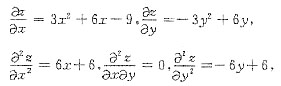
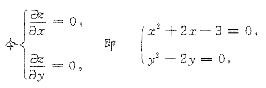
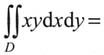 ______.
______.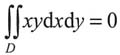 ,应选A.
,应选A.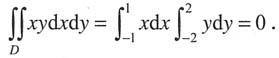
 ,所以原方程表示的是椭球面.
,所以原方程表示的是椭球面.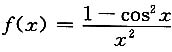 ,当x≠0时,F(x)=f(x),若F(x)在点x=0处连续,则F(0)等于______
,当x≠0时,F(x)=f(x),若F(x)在点x=0处连续,则F(0)等于______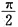

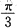
 ,则y'=______
,则y'=______
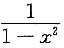
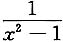
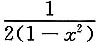
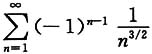 是______
是______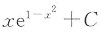
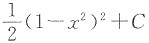
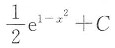
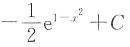
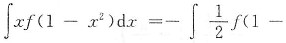
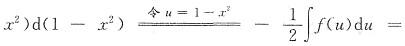
 .
.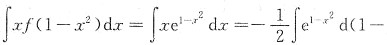
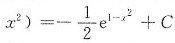 .
.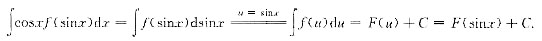
 则f(x)在______.
则f(x)在______.
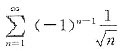
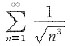
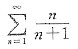
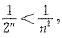 故选项A收敛;
故选项A收敛;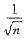 单调递减且
单调递减且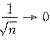 (n→∞),故选项B收敛;
(n→∞),故选项B收敛;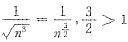 ,所以选项C收敛;
,所以选项C收敛;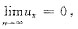 而
而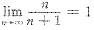 ,故选项D发散.
,故选项D发散.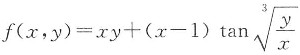 ,则fy(1,0)等于______
,则fy(1,0)等于______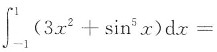
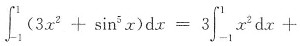
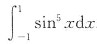 .因为f1(x)=x2为偶函数,所以
.因为f1(x)=x2为偶函数,所以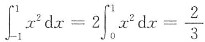 .因为f2(x)=sin5x为奇函数,所以
.因为f2(x)=sin5x为奇函数,所以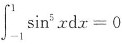 .故
.故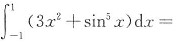
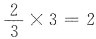 .
.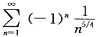 ______
______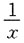
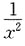
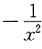
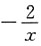
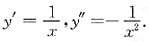 故选C.
故选C.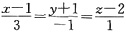 的位置关系是______
的位置关系是______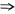 n⊥s,即直线l与平面π平行.
n⊥s,即直线l与平面π平行.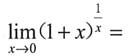 ______.
______.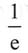
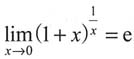 ,所以选D.
,所以选D.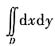 =______.
=______.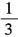

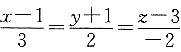 垂直的平面方程为______.
垂直的平面方程为______.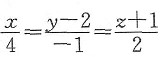
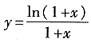 ,则y'|x=0=______.
,则y'|x=0=______.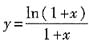 ,可知
,可知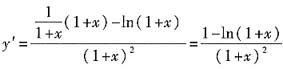 ,进而有y'|x=0=1.
,进而有y'|x=0=1.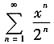 的收敛区间为______.
的收敛区间为______.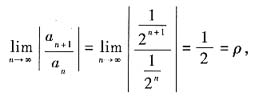
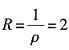 ,收敛区间为(-2,2).
,收敛区间为(-2,2).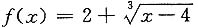 的拐点是______.
的拐点是______.
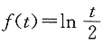 =ln t-1n 2,从而f(x)=ln x-ln 2,
=ln t-1n 2,从而f(x)=ln x-ln 2,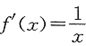 .
.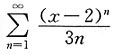 的收敛区间为______.(不包括端点)
的收敛区间为______.(不包括端点)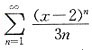 的一般项
的一般项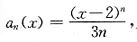 则由比值法有:
则由比值法有: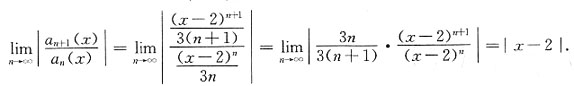
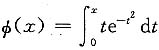 ,则当x=______时,
,则当x=______时, 取极______值.
取极______值.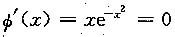 ,则x=0为
,则x=0为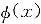 的驻点.
的驻点. ,故当x=0时,
,故当x=0时,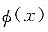 取极小值.
取极小值.