一、选择题2. 若
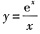
,则dy等于______.
A.
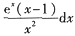
B.
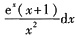
C.e
xdx
D.e
xlnxdx
A B C D
A
[解析] 本题可用dy=y'dx求得选项为A,也可以直接求微分得到dy.
因为
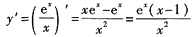
,
则
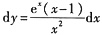
.
直接求微分得
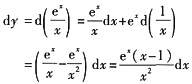
,所以选A.
3. 设函数

在x=2处连续,则a=______
A.

B.
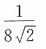
C.
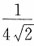
D.
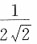
A B C D
B
[解析] 因为
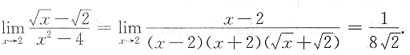
6. 设f(x)=x
3sinx,则
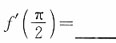
A.π
2 B.
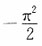
C.
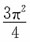
D.π-2
A B C D
C
[解析]
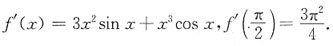
9. 设函数f(x)=x
3+e
3+3
x,则f'(x)等于______.
A.3x
2+3
xln3
B.3x
2+3e
2+x·3
x-1 C.
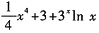
D.
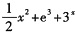
A B C D
A
[解析] 本题考查的知识点是基本初等函数的导数公式.只需注意e3是常数即可.
10. 设z=f(x
2-y
2),u=x
2-y
2,f(u)是可导函数,
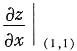
等于______
- A.f'(0)
- B.2f'(0)
- C.-f'(0)
- D.-2f'(0)
A B C D
B
[解析] 因
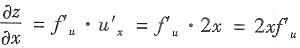
,则
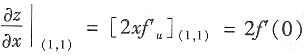
,故选B.
14. 甲、乙、丙三人独立地向目标射击一次,其命中率依次为0.5,0.6,0.7,则目标被击中的概率是______
A B C D
A
[解析] 设A
k表示第k人击中目标(k=1,2,3),目标被击中可表示为A
1+A
2+A
3.
已知P(A
1)=0.5,P(A
2)=0.6,P(A
3)=0.7,且A
1,A
2,A
3相互独立,所以

16. 设f(x)=ln2+e
3,则f'(x)=______
A.
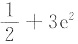
B.0
C.ln2+e
3 D.(ln2+3e
2)
A B C D
B
[考点] 本题考查了常数的导数的知识点.
f(x)=ln2+e3,由于ln2和e3均为常数,所以f'(x)=0.
17. 下面等式正确的是______.
A.e
xsin(e
x)dx=sin(e
x)d(e
x)
B.
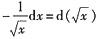
C.
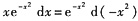
D.e
cosxsinxdx=e
cosxd(cosx)
A B C D
A
[解析] 将式中的微分计算出来,比较左、右两边的式子,可知选项A正确.
18. 下列函数中在点x=0处不连续的是______
A.
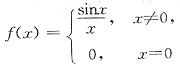
B.
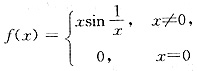
C.
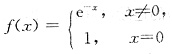
D.
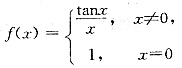
A B C D
A
[解析] 选项A中,f(0)=0,
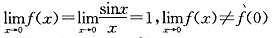
f(x)在点x=0处不连续;
选项B中,f(0)=0,
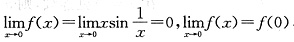
,f(x)在点x=0处连续;
选项C中,f(0)=1.
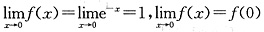
,f(x)在点x=0处连续;
选项D中,f(0)=1.
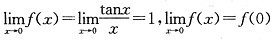
,f(x)在点x=0处连续.
20.
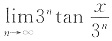
=______
A.

B.3x
C.x
D.3
A B C D
C
[考点] 本题考查了极限的知识点.
本题注意,变量是n而不是x.
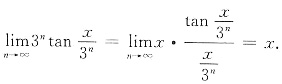
23. 二元函数z=(1+3x)
2y,则
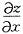
等于______
- A.2y(1+3x)2y-1
- B.6y(1+3x)2y-1
- C.(1+3x)2yln(1+3x)
- D.6y(1+3x)2y
A B C D
B
[解析]
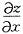
=2y(1+3x)
2y-1·3=6y(1+3x)
2y-1.
24. 函数
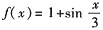
在点x=0处的导数是______.
A.0
B.
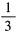
C.
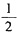
D.3
A B C D
B
[解析] 因为
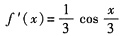
,
所以
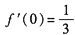
.
25. 要使
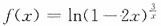
在x=0处连续,应补充f(0)等于______
A.e
-6 B.-6
C.
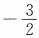
D.0
A B C D
B
[解析] ∵
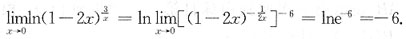
∴要使f(x)在x=0处连续,应补充f(0)=-6.
26. 设z=f(u,v),其中u=xy,v=y
2,且
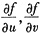
都存在,则
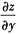
等于______.
A.
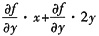
B.
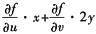
C.
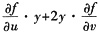
D.
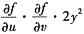
A B C D
B
[解析] 本题考查的知识点是二元复合函数的偏导数的计算.
28.

A.ln2
B.2ln2
C.

D.

A B C D
C
[考点] 本题考查了定积分的知识点.
[解析]

29. 若事件A发生必然导致事件B发生,则事件A和B的关系一定是______.
A.A
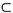
B
B.A
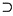
B
C.对立事件
D.互不相容事件
A B C D
A
[解析] 本题考查的知识点是事件关系的概念.
根据两个事件相互包含的定义,可知选项A正确.
30. 下列反常积分收敛的是
A.

B.

C.

D.

A B C D
C
[解析] A项:

发散;
B项:

发散;
C项:

发散;
D项:

发散.
二、填空题1. 设
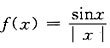
,则
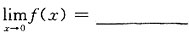
.
不存在
[解析] 由
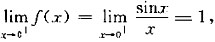
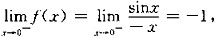
所以
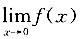
不存在.
注:对分段函数在分段点处求极限总是要从求其左、右极限入手进行讨论,若左、右极限存在且相等,则所求极限存在,否则所求极限不存在.
2. 设f(x)的n-1阶导数为
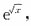
则f
(n)(x)=______.
[解析]
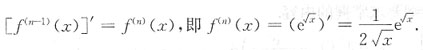
3.
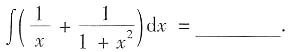
4. 袋中有编号为1~5的5个小球,现从中任意取2个,则两个球的编号都不大于3的概率为______。
5. 设函数
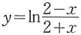
,则f"(1)=______。
[解析] f(x)=ln(2-x)-ln(2+x),
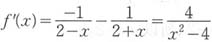
,
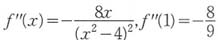
。
6. 设
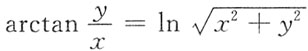
确定了y是x的函数,则y'=______.
[考点] 本题考查了隐函数的一阶偏导数的知识点.
[解析] 由
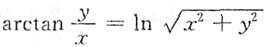
,两边对x求导有
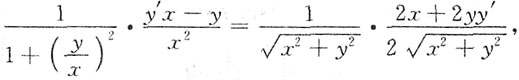
整理得
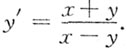
8. 设函数f(x)在x=2处连续,且

存在,则f(2)=______.
1
[解析] 因为

存在,所以f(x)-1→0,即f(x)→1(x→2).
因为f(x)在x=2处连续,所以f(2)=1.
9. 曲线
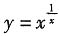
在点(1,1)处的切线方程是______,法线方程是______.
x-y=0 x+y-2=0
[解析]
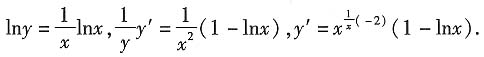
y'|
x=1=1,切线方程y-1=x-1,即x-y=0;
法线方程y-1=-(x-1),即x+y-2=0.
10. 函数
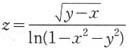
的定义域是______。
x2+y2≠0
[解析] 解不等式组
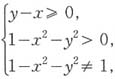
得
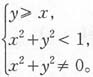
即y≥x,x
2+y
2<1,且x
2+y
2≠0。
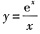 ,则dy等于______.
,则dy等于______.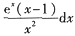
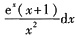
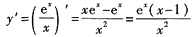 ,
,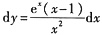 .
.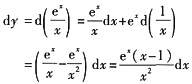 ,所以选A.
,所以选A. 在x=2处连续,则a=______
在x=2处连续,则a=______
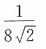
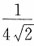
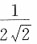
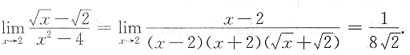
 ,则f'(x)=
,则f'(x)=
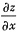 等于______.
等于______.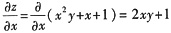 ,选B.
,选B.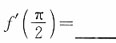
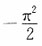
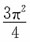
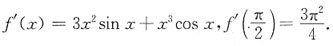
 ,则f'(x0)等于
,则f'(x0)等于 
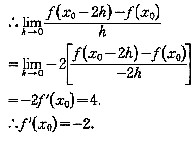
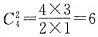 .
.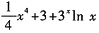
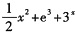
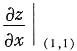 等于______
等于______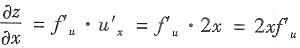 ,则
,则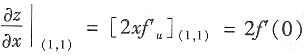 ,故选B.
,故选B.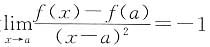 ,则在点x=a处______.
,则在点x=a处______.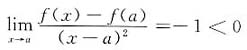
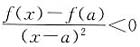 ,从而f(x)-f(a)<0,即f(x)<f(a).故f(x)取得极大值.
,从而f(x)-f(a)<0,即f(x)<f(a).故f(x)取得极大值.
 时,应视函数关系中的y为常数,于是,
时,应视函数关系中的y为常数,于是, ,故选D.
,故选D.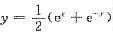 在区间(-1,1)内
在区间(-1,1)内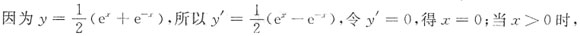

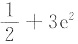
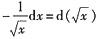
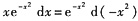
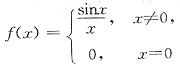
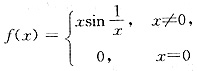
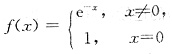
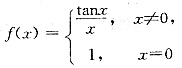
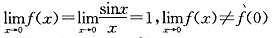 f(x)在点x=0处不连续;
f(x)在点x=0处不连续;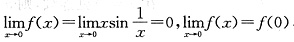 ,f(x)在点x=0处连续;
,f(x)在点x=0处连续;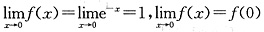 ,f(x)在点x=0处连续;
,f(x)在点x=0处连续;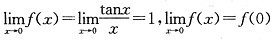 ,f(x)在点x=0处连续.
,f(x)在点x=0处连续.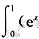 -1)dx=e-2.
-1)dx=e-2.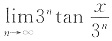 =______
=______
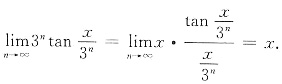
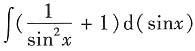 等于______
等于______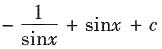
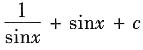
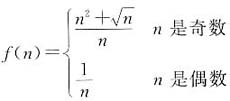 ,当n→∞时,f(n)是______.
,当n→∞时,f(n)是______.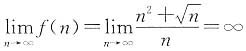 .
.
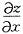 等于______
等于______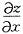 =2y(1+3x)2y-1·3=6y(1+3x)2y-1.
=2y(1+3x)2y-1·3=6y(1+3x)2y-1.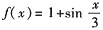 在点x=0处的导数是______.
在点x=0处的导数是______.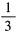
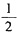
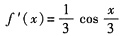 ,
,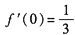 .
.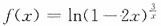 在x=0处连续,应补充f(0)等于______
在x=0处连续,应补充f(0)等于______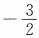
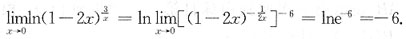
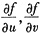 都存在,则
都存在,则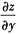 等于______.
等于______.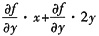
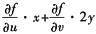
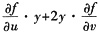
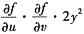
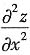 等于
等于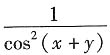
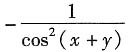
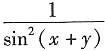
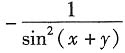




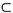 B
B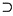 B
B



 发散;
发散; 发散;
发散; 发散;
发散; 发散.
发散.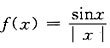 ,则
,则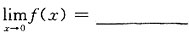 .
.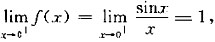
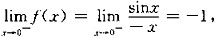
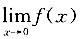 不存在.
不存在.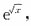 则f(n)(x)=______.
则f(n)(x)=______.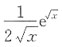
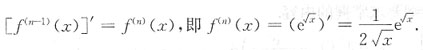
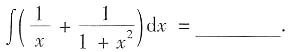
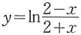 ,则f"(1)=______。
,则f"(1)=______。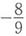
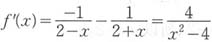 ,
,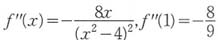 。
。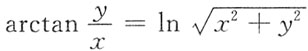 确定了y是x的函数,则y'=______.
确定了y是x的函数,则y'=______.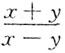
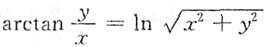 ,两边对x求导有
,两边对x求导有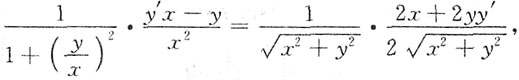 整理得
整理得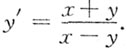
 存在,则f(2)=______.
存在,则f(2)=______. 存在,所以f(x)-1→0,即f(x)→1(x→2).
存在,所以f(x)-1→0,即f(x)→1(x→2).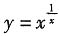 在点(1,1)处的切线方程是______,法线方程是______.
在点(1,1)处的切线方程是______,法线方程是______.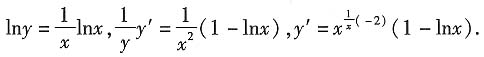
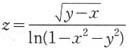 的定义域是______。
的定义域是______。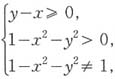 得
得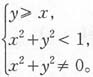 即y≥x,x2+y2<1,且x2+y2≠0。
即y≥x,x2+y2<1,且x2+y2≠0。