一、单项选择题4. 设实数a、b,若
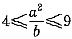
,3≤ab
2≤8,则
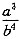
的最小值为______.
A B C D
A
[解析] 由题意可知,a、b均为正实数,则原不等式均可变为2lg2≤2lga-lgb≤2lg3,lg3≤lga+2lgb≤3lg2,又因为
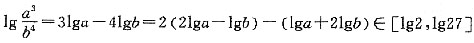
,即
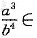
[2,27],故

的最小值为2.
12. 某学校为了美化环境,欲改造一块边长分别为48米、72米、84米、96米的四边形空地,其中一项是在空地四边种树,要求四个顶点上要各有一棵,并且每棵树的间距相同,请问最少要准备多少棵树苗? ______
A B C D
C
[解析] 由已知可得,要想种的树最少,则需求四个边长的最大公约数,这个最大公约数即为每棵树的间距.又因为48=3×2
4,72=2
3×3
2,84=2
2×3×7,96=2
5×3,故这四个数的最大公约数为12,即每棵树的间距为12米,所以需要树苗的最少量为
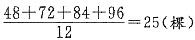
.
13. 同时掷两个骰子,各掷一次,向上的点数之和为6的概率是______
A.
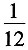
B.
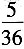
C.
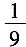
D.
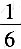
A B C D
B
[解析] 向上的点数之和为6有(1,5),(2,4),(3,3),(4,2)和(5,1)共5种情况,而事件总的可能性有6×6=36种,故所求概率为
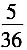
,选B。
14. 已知a、b为实数,则下列各式中一定是正值的是______.
A.a
2-2a+2
B.a
2+b
2 C.
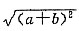
D.(a-1)
2+丨b+2丨
A B C D
A
[解析] A项可写为(a-1)2+1,其恒大于0,其他三项的值均为大于等于0,不一定是正值,故选A.故一定为正值.
18. 数列{a
n}为公差不为0的等差数列,其首项a
1为a(a∈R),且数列
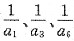
是等比数列,则数列{a
n}的通项公式为______.
A.

B.
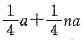
C.
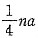
D.
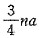
A B C D
A
[解析] 由数列
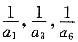
是等比数列得,
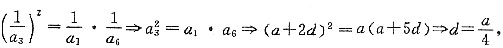
则数列{a
n}的通项公式为
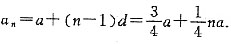
19. 已知abc>0,则在下列四个选项中,表示y
1,y
2,y
3图象的只可能是______.
A.
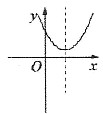
B.
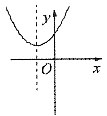
C.
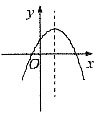
D.
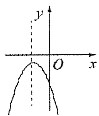
A B C D
B
[解析] 选项A,由图象开口向上可知,a>0,由f(0)=c>0,又抛物线对称轴
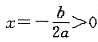
,所以b<0,则abc<0,不符合题意;选项B,由图象开口向上可知,a>0,由f(0)=c>0,又抛物线对称轴
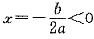
,所以b>0,abc>0,符合题意;同理可推出C、D均不符合题意.故答案选B.
21. 函数
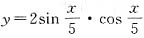
的最大值是______.
A.
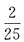
B.1
C.2
D.4
A B C D
B
[解析] 由三角函数公式得,

,则y=sint,故函数的最大值为1.
22. 已知2≤x-y≤3,且3≤x+y≤5,则3x+2y的取值范围为______。
A.[10,14]
B.
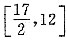
C.
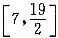
D.
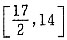
A B C D
D
[解析] 设3x+2y=a(x-y)+b(x+y)=(a+b)x+(b-a)y,由此可得
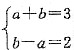
,解得
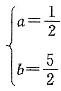
,所以
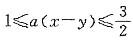
,
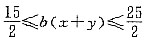
,即
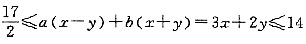
.
故3x+2y的取值范围为
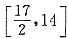
.
24. 已知a>b,则下列不等式不一定成立的是______.
A.a(m
2+1)>b(m
2+1)
B.a
2>b
2 C.a+m>b+m
D.
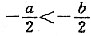
A B C D
B
[解析] 如果a=-3,b=-4,有a>b,但a2<b2,因此B选项不一定成立.
二、填空题1. 一个数除以9余8,除以6余5,这个数加上1就能被5整除,则符合条件的最小自然数是______。
89
[解析] 由题意知,该数加上1,可以被9,6,5整除。由9,6,5这三个数的最小公倍数是9×2×5=90,故符合条件的最小自然数是90-1=89。
2. 若
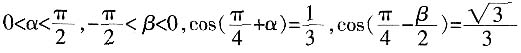
,则
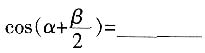
。
[解析]
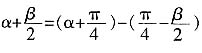
,然后根据两角差的余弦公式计算。
3. 《义务教育数学课程标准(2011年版)》强调学生的数学学习内容应当是现实的、______、______。
4. 已知函数f(x)=sinx,g(x)=x
2+ax+2,如果对于任意的x
1∈[0,2π],都存在x
2∈R使得f(x
1)=g(x
2)成立,则a的取值范围是______。
[解析] 由题意可知[f(x)]
min≥[g(x)]
min,即
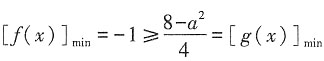
,解得
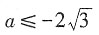
或
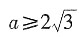
。
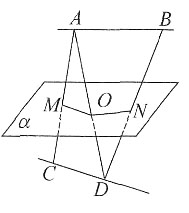
5. 如图所示,AB∥α,CD∥α,AC,BD分别交α于M,N两点,
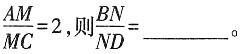

2
[解析] 如图所示,连结AD,交平面α于O,连结OM,ON。∵AB∥α,CD∥α,AC,BD分别交α于M,N两点,∴OM∥CD,ON∥AB,
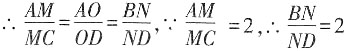
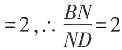
。
6. 一个正方体的各顶点均在同一球的球面上,若该球的体积为

,则该正方体的表面积为______。
24
[解析] 设球的半径为R,正方体的棱长为a。由

,故a=2,表面积为6a
2=24。
7. 如图所示,l
1是反比例函数
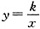
在第一象限内的图象,且过点A(2,1),l
2与l
1关于x轴对称,那么图象l
2的函数解析式为______(x>0)。
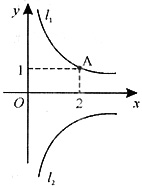
[解析] 本题考查平面直角坐标系中点的对称及待定系数法,将点A(2,1)代入函数
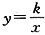
得:k=2,所以图象l
2的函数解析式为
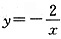
。
8. 已知f(x)=6-12x+x
3,
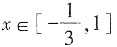
,则函数的最大值为______,最小值为______。
[解析] f'(x)=3x
2-12。当
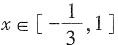
时,f'(x)<0,则在区间
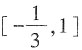
上,函数f(x)是单调减函数。又
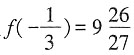
,f(1)=-5,则当
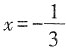
时,
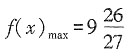
,当x=1时,f(x)
min=-5。
9. 命题“若ab=0,则a=0”的否命题是______。
若ab≠0,则a≠0
[解析] 求命题的否命题时,要将原命题的条件和结论都否定。
10. 观察下列等式:
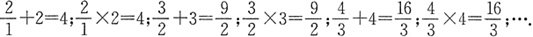
根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______.
[解析] 由于
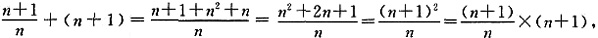
所以,
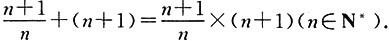
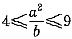 ,3≤ab2≤8,则
,3≤ab2≤8,则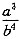 的最小值为______.
的最小值为______.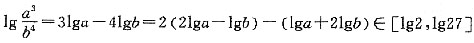 ,即
,即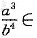 [2,27],故
[2,27],故 的最小值为2.
的最小值为2.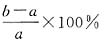
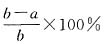
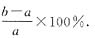
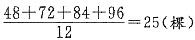 .
.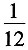
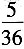
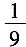
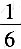
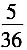 ,选B。
,选B。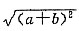
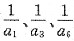 是等比数列,则数列{an}的通项公式为______.
是等比数列,则数列{an}的通项公式为______.
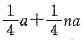
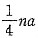
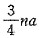
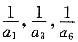 是等比数列得,
是等比数列得,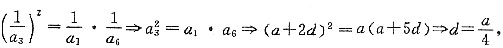 则数列{an}的通项公式为
则数列{an}的通项公式为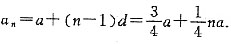




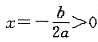 ,所以b<0,则abc<0,不符合题意;选项B,由图象开口向上可知,a>0,由f(0)=c>0,又抛物线对称轴
,所以b<0,则abc<0,不符合题意;选项B,由图象开口向上可知,a>0,由f(0)=c>0,又抛物线对称轴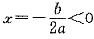 ,所以b>0,abc>0,符合题意;同理可推出C、D均不符合题意.故答案选B.
,所以b>0,abc>0,符合题意;同理可推出C、D均不符合题意.故答案选B.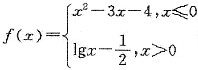 的零点个数为______.
的零点个数为______.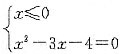 或
或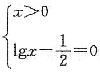 ,解得x=-1或
,解得x=-1或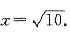 故函数f(x)的零点个数为2.
故函数f(x)的零点个数为2.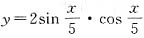 的最大值是______.
的最大值是______.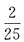
 ,则y=sint,故函数的最大值为1.
,则y=sint,故函数的最大值为1.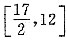
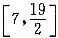
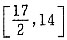
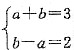 ,解得
,解得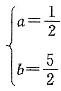 ,所以
,所以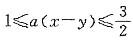 ,
,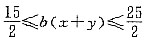 ,即
,即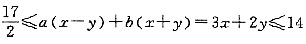 .
.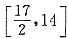 .
.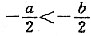
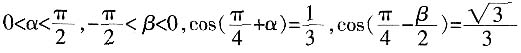 ,则
,则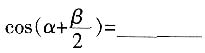 。
。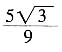
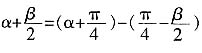 ,然后根据两角差的余弦公式计算。
,然后根据两角差的余弦公式计算。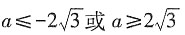
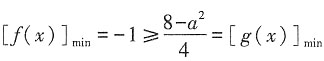 ,解得
,解得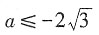 或
或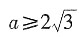 。
。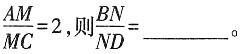

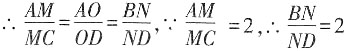
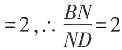 。
。
 ,则该正方体的表面积为______。
,则该正方体的表面积为______。 ,故a=2,表面积为6a2=24。
,故a=2,表面积为6a2=24。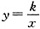 在第一象限内的图象,且过点A(2,1),l2与l1关于x轴对称,那么图象l2的函数解析式为______(x>0)。
在第一象限内的图象,且过点A(2,1),l2与l1关于x轴对称,那么图象l2的函数解析式为______(x>0)。

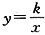 得:k=2,所以图象l2的函数解析式为
得:k=2,所以图象l2的函数解析式为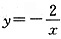 。
。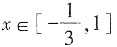 ,则函数的最大值为______,最小值为______。
,则函数的最大值为______,最小值为______。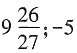
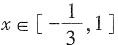 时,f'(x)<0,则在区间
时,f'(x)<0,则在区间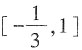 上,函数f(x)是单调减函数。又
上,函数f(x)是单调减函数。又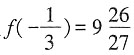 ,f(1)=-5,则当
,f(1)=-5,则当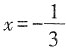 时,
时,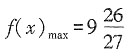 ,当x=1时,f(x)min=-5。
,当x=1时,f(x)min=-5。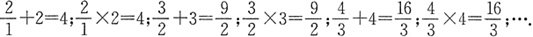 根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______.
根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______.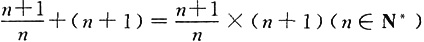
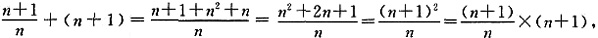 所以,
所以,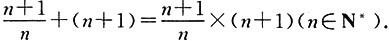
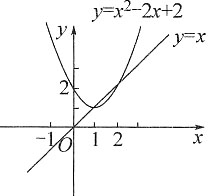
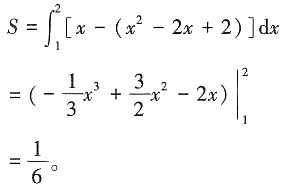
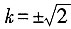 时,方程有一个根,l与C有一个交点;
时,方程有一个根,l与C有一个交点;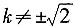 时,Δ=[2(k2-2k)]2-4(2-k2)(-k2+4k-6)=16(3-2k)。
时,Δ=[2(k2-2k)]2-4(2-k2)(-k2+4k-6)=16(3-2k)。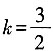 时,方程有一个实根,l与C有一个交点。
时,方程有一个实根,l与C有一个交点。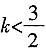 ,且
,且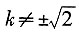 ,故当
,故当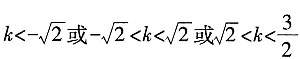 时,方程有两不等实根,l与C有两个交点。
时,方程有两不等实根,l与C有两个交点。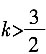 时,方程无解,l与C无交点。
时,方程无解,l与C无交点。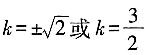 或k不存在时,l与C只有一个交点;当
或k不存在时,l与C只有一个交点;当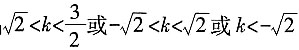 时,l与C有两个交点;当
时,l与C有两个交点;当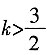 时,l与C没有交点。
时,l与C没有交点。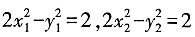 ,两式相减得2(x1-x2)(x1+x2)=(y1-y2) (y1+y2)。
,两式相减得2(x1-x2)(x1+x2)=(y1-y2) (y1+y2)。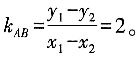
 ,结合图形知直线AB与C无交点,故假设不正确,即以Q为中点的弦不存在。
,结合图形知直线AB与C无交点,故假设不正确,即以Q为中点的弦不存在。