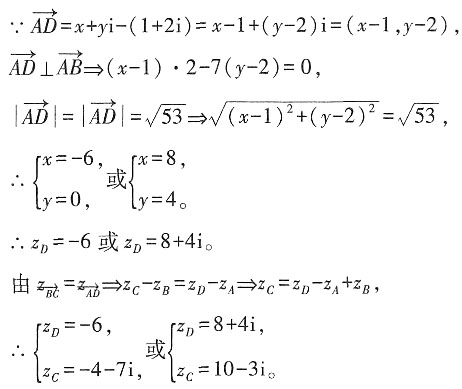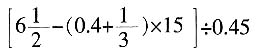一、单项选择题7. 已知集合U={x丨-3<x<5,x∈N
*},A={x丨(x-1)
2<4,x∈R},B={-2,-1,0,1,2,3,4},
则
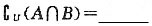
.
- A.{-2,4,5}
- B.{-2,-1,3,4}
- C.{-2,-1,3,4,5}
- D.{-2,3,4,5}
A B C D
B
[解析] 根据题意,U={-2,-1,0,1,2,3,4},A={-1<x<3},则A∩B={-1<x<3}∩{-2,-1,0,1,2,3,4}={0,1,2},因此
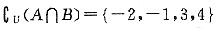
.
9. 设等比数列{a
n}的前n项和为S
n,已知4a
3-a
5=0,则
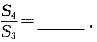
A.
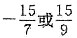
B.
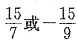
C.
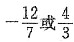
D.
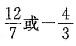
A B C D
B
[解析] 设等比数列的首项为a
1,公比为q,则4a
3-a
5=0整理可得4a
3-a
3q
2=0,解得q=±2.当q=2时,
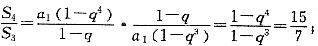
当q=-2时,
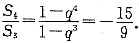
故答案选B.
18. 从编号为1、2、…、10的10个大小相同的球中任取4个,则所取4个球的最大号码是6的概率为______
A.
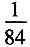
B.
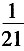
C.
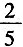
D.
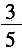
A B C D
B
[解析] 要使所取4个球的最大号码是6,一定有一个球的号码是6,其他三个球从1至5号球中选,有
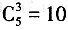
(种)选法,而从10个球选4个球的方法共
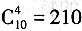
(种)选法,所以概率
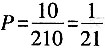
,故选B。
22. 设函数f(x)在[a,b]上连续,则曲线y=f(x)与直线x=a,x=b,y=0所围成的平面图形的面积为______.
A.
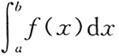
B.
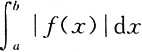
C.
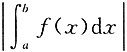
D.f(ξ)(b-a)(a<ξ<b)
A B C D
B
[解析] 根据定积分在几何中求平面图形的面积的应用可知,所围成平面图形的面积为
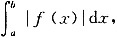
选B.
24. 将函数
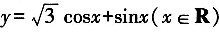
的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是______
A.
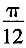
B.
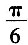
C.
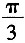
D.
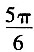
A B C D
B
[解析]
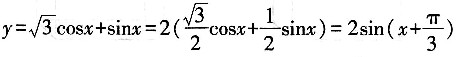
,则图象向左平移m(m>0)个单位长度得到
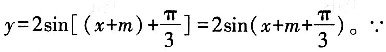
所得的图象关于y轴对称,
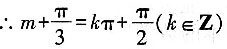
∴m的最小值为
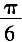
。
二、填空题1. 若对任意x>0,
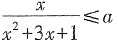
恒成立,则a的取值范围是______。
[解析] 由题意,得
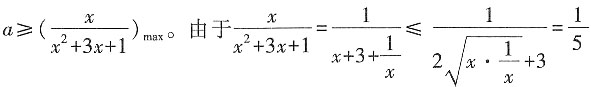
,当且仅当x=1时,取等号。所以
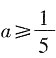
。
2. 如果将一根木料锯成3段,小明要用6分钟,爸爸锯木料的速度是小明的3倍,由爸爸将这根木料锯成5段,需要______分钟。
4
[解析] 小明锯一次需3分钟,小明爸爸锯一次需1分钟。锯成5段需要锯4分钟。
3. 若实数x,y满足
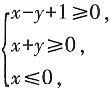
则z=x+2y的最小值是______。
0
[解析] 本小题主要考查线性规划问题。作图易知可行域为一个三角形,其三个顶点分别为(0,0)、(0,1)、
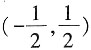
,验证知z=x+2y在点(0,0)时取得最小值0。
4. 用0,1,2,3,4这5个数字中的4个组成的4位数中,能被6整除的数有______个.
24
[解析] 整数能被6整除,则其个位为偶数,且每一位上的数字之和能被3整除.0,1,2,3,4中的四个数的和能被3整除,则只有两种可能:0,1,2,3和0,2,3,4;另外,还要千位不能为0,个位为偶数.当取0,1,2,3四个数字时:①2在千位,则0一定在个位,故有
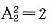
种排法;②2不在千位上,则要从1,3之中取一个数字放在千位,再从0,2之中取一个数字放在个位,其他任排,故有
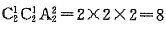
种排法.当取0,2,3,4四个数字时:①3在千位时,其他位可任排,故有
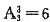
种排法;②3不在千位时,从2,4中取一个数字放在千位,在从剩下的两个偶数中取一个放在个位,其他任排,故有
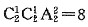
种排法.所以能被6整除的数共有2+8+6+8=24(个).
5. 数列{a
n}是公差不为0的等差数列,a
1=1,a
3是a
1,a
9的等比中项,则数列{a
n}的通项公式为______。
an=n
[解析] 设数列{an}的公差为d。由题意得(1+2d)2=1×(1+8d),解得d=1,故数列{an}的通项公式an=1+(n-1)×1=n。
6. 已知二次函数y=kx
2-2x-5的图象与x轴有交点,则k的取值范围为______。
7. x、y、z∈R
*,x-2y+3z=0,
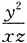
的最小值为______.
3
[解析] 由x-2y+3z=0得
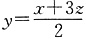
,代入
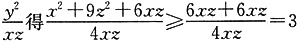
,当且仅当x=3z时取“=”.
8. 若AP垂直于正方形ABCD所在平面,且AB=AP=2,则PC=______。
[解析] ∵AP垂直于正方形ABCD所在平面,且AB=AP=2,∴
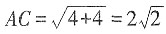
,PA⊥AC,∴
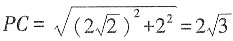
。
9. 一次大型运动会上,工作人员按照3个红气球,2个黄气球,1个绿气球的顺序把气球穿起来装饰运动场,那么第2013个气球是______色的(填“红”“黄”或“绿”)。
红
[解析] 根据题干可得,这组气球的排列规律是:6个气球一个循环周期,分别按照3红、2黄、1绿的顺序依次循环排列。由2013÷6=335……3,故第2013个气球是第336周期的第3个,是红气球。
10. (1+2x)
6的展开式中x
4的系数是______.
240
[解析] 二项展开式的通项公式
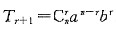
,则x
4的系数是
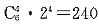
.
三、解答题在长方体ABCD-A1B1C1D1中,AA1=AD=1,AB=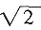 ,O为对角线A1C的中点。
,O为对角线A1C的中点。1. 求OD与底面ABCD所成的角的大小;
连接AC、BD交于点E,由
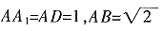
,则
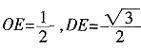
,故
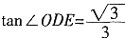
,即
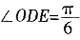
,故OD与底面所成的角为
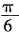
。
2. P为AB上一动点,当P在何处时,平面POD⊥平面A
1CD?并证明你的结论。
由
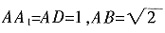
,则
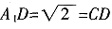
,又O为A
1C的中点,则OD⊥A
1C,于是当P为AB的中点时,
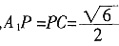
,从而OP⊥A
1C,故A
1C⊥平面POD。又
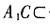
平面A
1OD,则平面PDD⊥平面A
1OD。
3. 在复平面上,正方形ABCD的两个顶点A,B对应的复数分别为1+2i,3-5i。求另外两个顶点C,D对应的复数。
解:设D(x,y)。
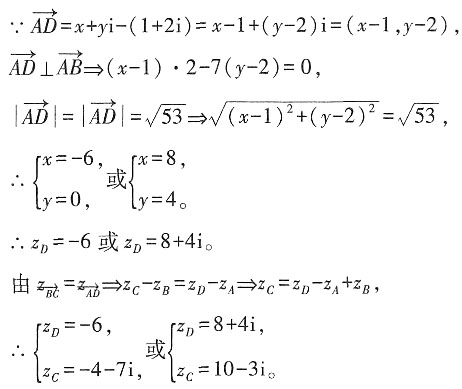
4. 脱式计算(能简算的要简算)
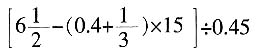
5. 求证:对于任意实数m,方程总有两个不相等的实数根;
证明:原方程可化为x2-5x+6-|m|=0。①
∴A=(-5)2-4×1×(6-|m|)=25-24+4|m|=1+4|m|。
∵|m|≥0,
∴+4|m|>0。
∴对于任意实数m,方程总有两个不相等的实数根。
6. 若方程的一个根是1,求m的值及方程的另一个根。
解:把x=1代入第一小题方程①,得|m|=2。
∴m=±2。
把|m|=2代入原方程,得x2-5x+4=0,
∴x1=1,x2=4。
∴m的值为±2,方程的另一个根是4。
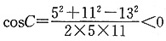 ,所以角C为钝角。故选C。
,所以角C为钝角。故选C。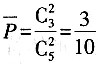 ,则所求概率
,则所求概率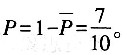
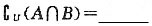 .
.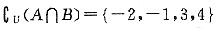 .
.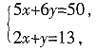
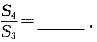
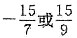
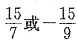
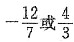
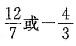
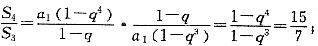 当q=-2时,
当q=-2时,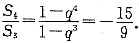 故答案选B.
故答案选B.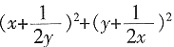 的最小值是______。
的最小值是______。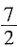

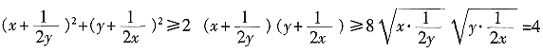 ,当且仅当
,当且仅当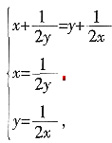 ,即
,即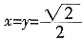 时等号成立。
时等号成立。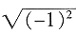 和-1
和-1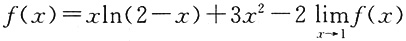 ,则
,则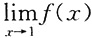 等于______.
等于______.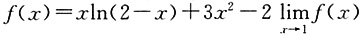 两边同时取极限为:
两边同时取极限为: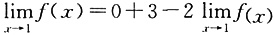 ,即
,即 ,故
,故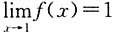 .故选C.
.故选C.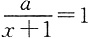 的解是负数,则a的取值范围是______.
的解是负数,则a的取值范围是______.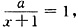 得x=a-1,因为方程的解是负数,所以a-1<0,所以a<1,又因为x+1≠0,所以a-1+1≠0,所以a≠0,所以a<1且a≠0,故选B.
得x=a-1,因为方程的解是负数,所以a-1<0,所以a<1,又因为x+1≠0,所以a-1+1≠0,所以a≠0,所以a<1且a≠0,故选B.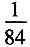
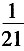
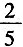
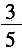
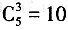 (种)选法,而从10个球选4个球的方法共
(种)选法,而从10个球选4个球的方法共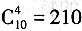 (种)选法,所以概率
(种)选法,所以概率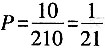 ,故选B。
,故选B。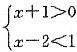 的解集是______.
的解集是______.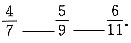
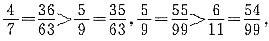
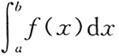
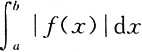
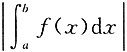
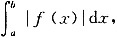 选B.
选B.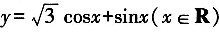 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是______
的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是______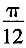
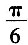
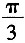
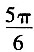
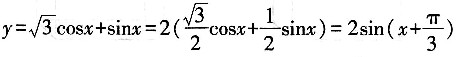 ,则图象向左平移m(m>0)个单位长度得到
,则图象向左平移m(m>0)个单位长度得到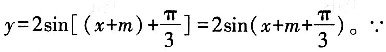 所得的图象关于y轴对称,
所得的图象关于y轴对称,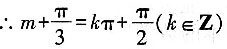 ∴m的最小值为
∴m的最小值为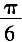 。
。
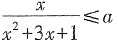 恒成立,则a的取值范围是______。
恒成立,则a的取值范围是______。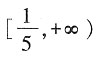
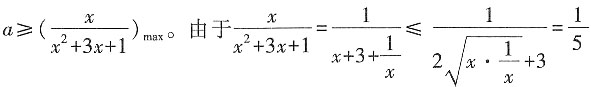 ,当且仅当x=1时,取等号。所以
,当且仅当x=1时,取等号。所以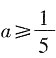 。
。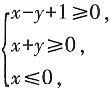 则z=x+2y的最小值是______。
则z=x+2y的最小值是______。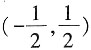 ,验证知z=x+2y在点(0,0)时取得最小值0。
,验证知z=x+2y在点(0,0)时取得最小值0。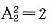 种排法;②2不在千位上,则要从1,3之中取一个数字放在千位,再从0,2之中取一个数字放在个位,其他任排,故有
种排法;②2不在千位上,则要从1,3之中取一个数字放在千位,再从0,2之中取一个数字放在个位,其他任排,故有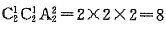 种排法.当取0,2,3,4四个数字时:①3在千位时,其他位可任排,故有
种排法.当取0,2,3,4四个数字时:①3在千位时,其他位可任排,故有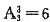 种排法;②3不在千位时,从2,4中取一个数字放在千位,在从剩下的两个偶数中取一个放在个位,其他任排,故有
种排法;②3不在千位时,从2,4中取一个数字放在千位,在从剩下的两个偶数中取一个放在个位,其他任排,故有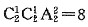 种排法.所以能被6整除的数共有2+8+6+8=24(个).
种排法.所以能被6整除的数共有2+8+6+8=24(个).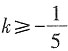 且k≠0
且k≠0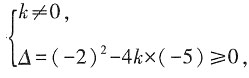 解得
解得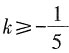 且k≠0。
且k≠0。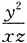 的最小值为______.
的最小值为______.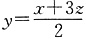 ,代入
,代入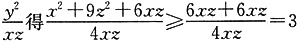 ,当且仅当x=3z时取“=”.
,当且仅当x=3z时取“=”.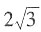
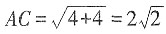 ,PA⊥AC,∴
,PA⊥AC,∴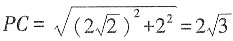 。
。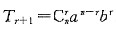 ,则x4的系数是
,则x4的系数是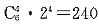 .
.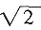 ,O为对角线A1C的中点。
,O为对角线A1C的中点。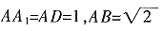 ,则
,则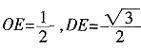 ,故
,故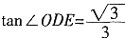 ,即
,即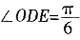 ,故OD与底面所成的角为
,故OD与底面所成的角为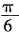 。
。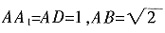 ,则
,则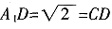 ,又O为A1C的中点,则OD⊥A1C,于是当P为AB的中点时,
,又O为A1C的中点,则OD⊥A1C,于是当P为AB的中点时,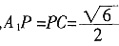 ,从而OP⊥A1C,故A1C⊥平面POD。又
,从而OP⊥A1C,故A1C⊥平面POD。又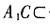 平面A1OD,则平面PDD⊥平面A1OD。
平面A1OD,则平面PDD⊥平面A1OD。