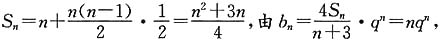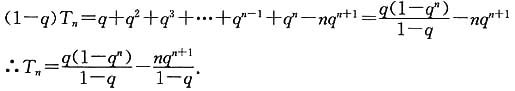一、单项选择题1. 已知圆的方程为(x-3)
2+(y-1)
2=9,现有一直线与圆相切,切点为
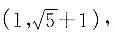
则直线方程为______.
A.
B.

C.
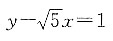
D.
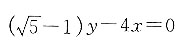
A B C D
B
[解析] 过圆(x-3)
2+(y-1)
2=9上的点
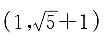
的切线方程是:
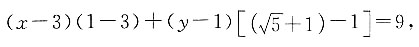
即
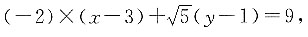
整理可得,
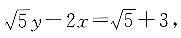
即为过点
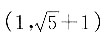
与圆相切的直线方程.
4. 已知二次型
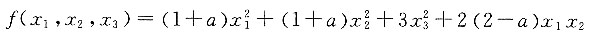
的秩为2,则a的值为______.
A.
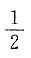
B.-1
C.2
D.-7
A B C D
A
[解析] 二次型矩阵

.二次型的秩为2,即矩阵的秩为2,所以
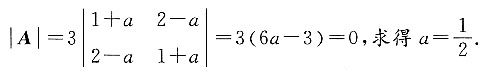
5. 在△ABC中,∠A=120°,AB=5,BC=7,则
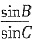
的值为______.
A.
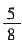
B.
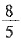
C.
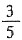
D.
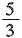
A B C D
C
[解析] 由余弦定理得,BC
2=AC
2+AB
2-2AC·ABcosA,即49=AC
2+25-2×5×ACcos120°,解得AC=3.根据正弦定理,
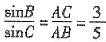
.
6. 若
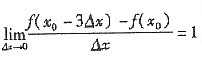
,则f′(x
0)=______.
A.1
B.
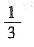
C.3
D.
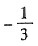
A B C D
D
[解析] ∵
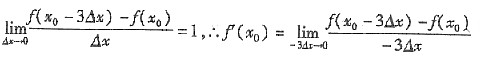
=
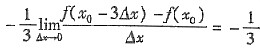
.故选D.
9. sin15°cos75°-cos15°sin75°=______.
A.
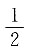
B.
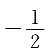
C.
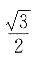
D.
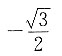
A B C D
D
[解析]
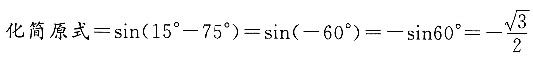
,因此本题选D.
10. 参数方程

(θ为参数)所表示的曲线为______.
A B C D
A
[解析] 本题考查直角坐标方程与参数方程的转化.同睼同意得,
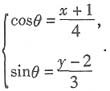
又因为cos
2θ+sin
2θ=1,则
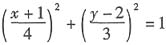
,即
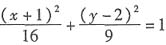
,表示的是椭圆.如对各种圆锥曲线的参数方程非常熟悉,也可直接判断.
14. 某班共有50名学生,其中戴眼镜的学生有10名,教师随机先后两次叫学生发言,且每次只叫一名学生,则两次叫到的学生都戴眼镜的概率为______.
A.
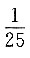
B.

C.
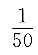
D.1
A B C D
A
[解析] 依题意,每次叫到戴眼镜学生的概率为
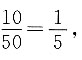
老师两次叫学生发言的事件相互独立,所以概率为
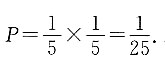
本题应注意老师两次叫的学生可能为同一人.
16. 已知函数

若f(2-x
2)>f(x),则实数x的取值范围是______
- A.(-∞,-1)∪(2,+∞)
- B.(-∞,-2)∪(1,+∞)
- C.(-1,2)
- D.(-2,1)
A B C D
D
[解析] 当
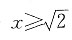
时,2-x
2≤0,有(2-x
2)
3>ln(x+1),此时因为(2-x
2)
3≤0,ln(x+1)>0,所以不等式无解;当
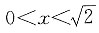
时,2-x
2>0,有ln(2-x
2+1)>ln(x+1),等价于
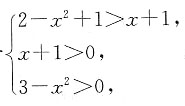
解得-1<x<1,结合前提条件得0<x<1;当
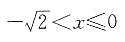
时,2-x
2>0,有ln(2-x
2+1)>x
3,此时因为ln(2-x
2+1)=ln(3-x
2)>ln 1=0,x
3≤0,不等式恒成立,故有
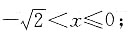
当

时,2-x
2≤0,有(2-x
2)
3>x
3,即2-x
2>x,解得-2<x<1,结合前提条件得
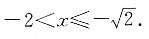
综上,得-2<x<1.
18. 已知等差数列{a
n}的前几项和为S
n,且a
1=
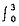
(1+2x)dx,a
2=5,则S
3为______.
A B C D
A
[解析] a
1=
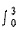
(1+2x)dx=(x+x
2)
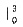
=12,d=a
2-a
1=5-12=-7,则a
3=a
2+d=5-7=-2,S
3=12+5-2=15.
22. 某班照合影,要求第一排站9人,第二排站10人,第三排站11人,班主任必须站在第一排的中间,则可能的站法有______种.
A.
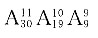
B.
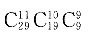
C.
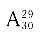
D.
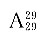
A B C D
D
[解析] 根据题意该班人数为11+10+9-1=29人,本题等价于29名学生站成一排的情况,有
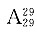
种,班主任插在第一排中间,不影响排列结果.
24. 设D、E、F分别是△ABC的三边BC、CA、AB上的点,且
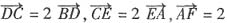
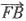
,则
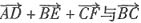
______.
- A.反向平行
- B.同向平行
- C.互相垂直
- D.既不平行也不垂直
A B C D
A
[解析] 由定比分点的向量式得:
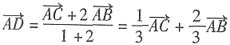
,同理得
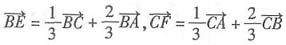
,以上三式相加得
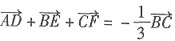
,所以选A.
26. 若不等式组
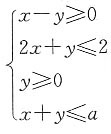
表示的平面区域是一个三角形,则a的取值范围是______
A.
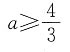
B.0<a≤1
C.
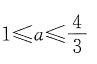
D.
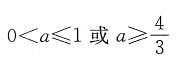
A B C D
D
[解析] 不等式纽

表示的平面区域如图所示(阴影部分).解
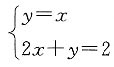
得
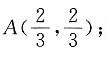
解
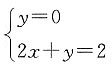
得B(1,0).若原不等式组表示的平面区域是一个三角形,则直线x+y=a中的a的取值范围是0<a≤1或
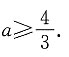
27. 定义平面向量之间的一种运算“

”如下,对任意的m=(a,b),n=(c,d),令
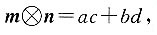
则下列说法错误的是______.
A.
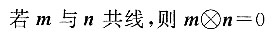
B.
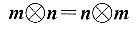
C.
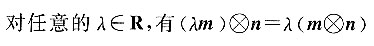
D.
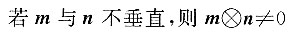
A B C D
A
[解析] 若m与n共线,则ad-bc=0,故A错误.其他三项中的运算均正确.
二、填空题1. 在使用等比数列求和公式时,分为q=1和q≠1两种情况,这种方法属于______.
分类讨论
[解析] 在使用等比数列求和公式时,应考虑当q的取值不同时,所运用的公式也不同,故需要根据不同的条件进行分类讨论.
2. 在平面直角坐标系中,已知两点A(1,2),B(3,-1),O为坐标原点,若点C(x,y)满足
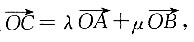
其中λ+μ=1,则点C的轨迹方程是______.
3x+2y-7=0
[解析] 由题,根据三点共线定理可知,A,B,C三点共线.因此点C的轨迹是A,B所在的直线,故点C的轨迹方程是

即3x+2y-7=0.
3. 已知向量a=(1,2),b=(-2,3),若ka+b与a-kb垂直,则实数k的值等于______.
[解析] ka+b=k(1,2)+(-2,3)=(k-2,2k+3),a-kb=(1,2)-k(-2,3)=(1+2k,2-3k),由ka+b与a-kb垂直可知(k-2)(1+2k)+(2k+3)(2-3k)=0,即k
2+2k-1=0,解得
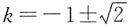
.
4. 半径为4的球O中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是______.
32π
[解析] 设球的一条半径与圆柱相应的母线夹角为α,网柱侧面积S=2π×4sinα×2×4cosα=32πsin2α,当
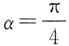
时,S取最大值32π,此时球的表面积与该圆柱的侧面积之差为32π.
5. 设A为n阶矩阵,|A|=3,则|2A*|=______.
[解析]
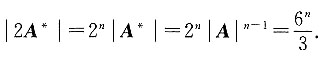
6. 已知数列1,2,2,3,3,3,4,4,4,4,…,则数字12第一次出现是在第______项.
67
[解析] 根据题意可知,数字1第一次出现是在第1项;数字2第一次出现是在第2项;数字3第一次出现是在第4项,数字4第一次出现是在第7项.用n来表示数字,用a
n来表示数字第一次出现时的项数.依据题中规律可得到:a
n-a
n-1=n-1,a
n-1-a
n-2=n-2,…,a
2-a
1=1.各项左右相加,可得
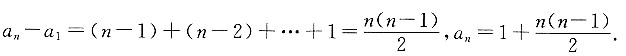
当n=12时,a
12=67.
7. 甲与乙两人分别做一批零件,且相互独立,甲、乙都在规定时间内做完的概率为0.64,且甲在规定时间内做完而乙没有做完的概率与乙在规定时间内做完而甲没有做完的概率相等,则甲、乙都没有在规定时间内做完这批零件的概率为______.
0.04
[解析] 设甲在规定时间内做完零件的概率为p,乙在规定时间内做完零件的概率为q,依题意,p·q=0.64,p(1-q)=q(1-p).即p=q,所以p=q=0.8,所以甲、乙都没有在规定时间内做完这批零件的概率为(1-p)(1-q)=0.04.
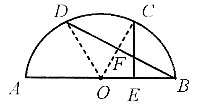
8. 如图所示,C、D是半圆上两个点,
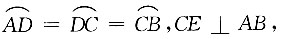
垂足为E,与BD交于F,已知
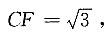
则⊙O的直径为______.
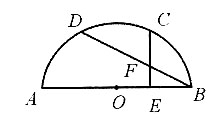
6
[解析] 如图所示,连接OC、OD,设⊙O的半径为r,因为
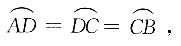
所以∠COB=∠DOA=60°,∠ABD=30°,因为CE⊥AB,OB=OC=r,所以
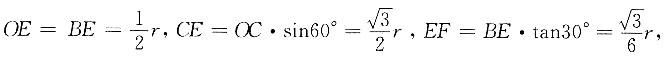
所以
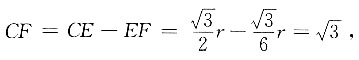
故r=3,直径d=2r=6.
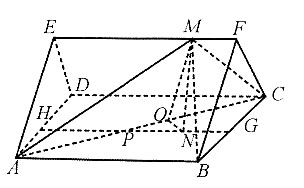
9. 如图,在正三棱柱ADE—BCF中,底面边长为4,ME=3MF,AB=4,则S
△ACM=______.
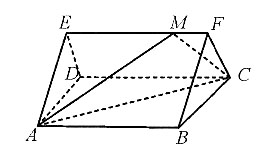
10
[解析] 方法一:取BC、AD中点G、H并连接,与AC交于P,M在面ABCD上的投影N在GH上.过N点作NO⊥AC,根据三垂线定理得,
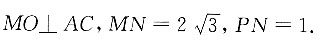
因为△PON∽△PGC,所以
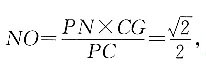
所以
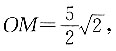
S
△ACM=10.
方法二:因为EF⊥AE,AB⊥BC,EF⊥CF,
即△AEM、△MFC、△ABC为直角三角形,因为△BCF为边长为4的正三角形,
ME=3MF,AB=4,所以
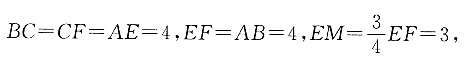
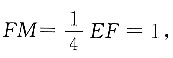
在Rt△AEM、Rt△MFC、Rt△ABC中,
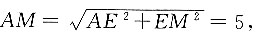

利用余弦定理,
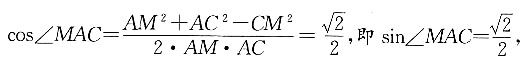
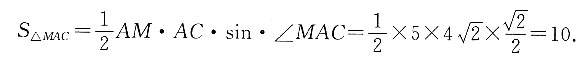
10. 教师的根本任务是______.教师在教育过程中起______作用.
三、解答题1. 求函数
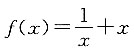
在定义域(1,+∞)上的单调性.
方法一:
设x
1、x
2∈(1,+∞),且x
1<x
2.
所以
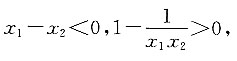
又
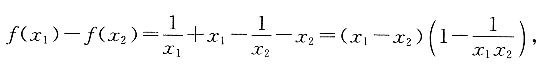
所以f(x
1)-f(x
2)<0,
即f(x
1)<f(x
2).
所以函数
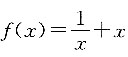
,在定义域(1,+∞)上单调递增.
方法二:
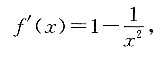
因为x∈(1,+∞),
所以
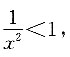
所以
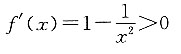
即函数
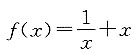
在定义域(1,+∞)上单调递增.
2. 在复平面内,z=a
2(1-i)+a(2+i)+1对应的点在第四象限,求a的取值范围.
原式化简得z=(a
2+2a+1)+(a-a
2)i
该复数在复平面内对应的点在第四象限,
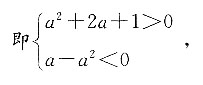
解得

因此的取值范围为(-∞,-1)∪(-1,0)∪(1,+∞).
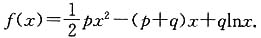 (其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(n,2Sn)(n∈N+)均在函数
(其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(n,2Sn)(n∈N+)均在函数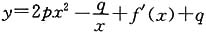 的图象上,(其中f'(x)是函数f(x)的导函数).
的图象上,(其中f'(x)是函数f(x)的导函数).3. 求a
1的值;
解:
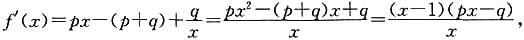
令f'(x)=0,得x=1或

当x的值变化时,f'(x),f(x)的变化情况如下表:
| |
 |
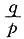 |
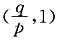 |
1 |
(1,+∞) |
|
| f'(x) |
+ |
0 |
- |
0 |
+ |
| f(x) |
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以f(x)在x=1处取得最小值,即a
1=1.
4. 求数列{a
n}的通项公式;
解:因为

所以
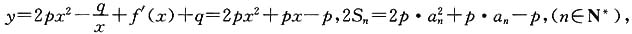
由于a
1=1,所以
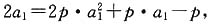
得p=1.
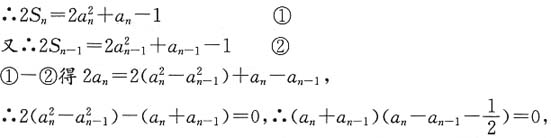
由于a
n+a
n-1>0,∴
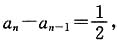
所以{a
n}是以a
1=1,公差为
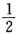
的等差数列,
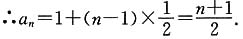
5. 记
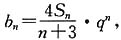
求数列{b
n}的前n项和T
n.
解:
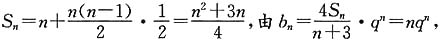
所以,T
n=q+2q
2+3q
3+…+(n-1)q
n-1+nq
n,由p>q>0,而p=1,故q≠1,
qT
n=q
2+2q
3+3q
4+…+(n-1)q
n+nq
n+1,
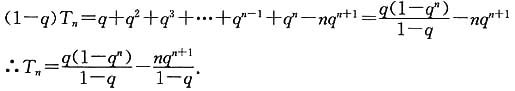
 则直线方程为______.
则直线方程为______.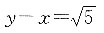

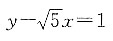
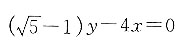
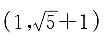 的切线方程是:
的切线方程是: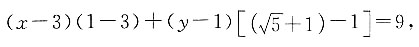 即
即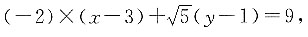 整理可得,
整理可得,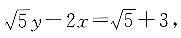 即为过点
即为过点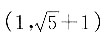 与圆相切的直线方程.
与圆相切的直线方程.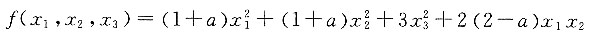 的秩为2,则a的值为______.
的秩为2,则a的值为______.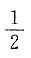
 .二次型的秩为2,即矩阵的秩为2,所以
.二次型的秩为2,即矩阵的秩为2,所以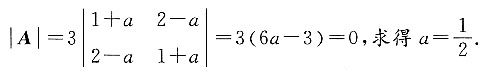
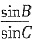 的值为______.
的值为______.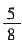
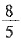
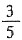
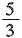
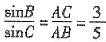 .
.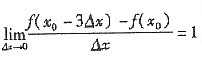 ,则f′(x0)=______.
,则f′(x0)=______.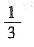
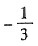
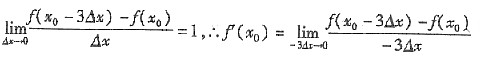
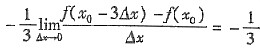 .故选D.
.故选D.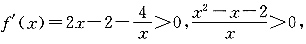 因为x>0,所以(x-2)(x+1)>0,所以x>2.
因为x>0,所以(x-2)(x+1)>0,所以x>2.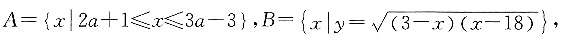 则“A∩B=A”的一个充分不必要条件是______.
则“A∩B=A”的一个充分不必要条件是______.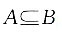 ,又
,又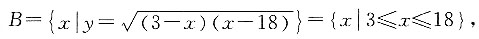 所以2a+1≥3且3a-3≤18,且3a-3≥2a+1,解得4≤a≤7.综合四个选项,只有“5<a<6”能推出“A∩B=A”,而由“A∩B=A”推不出“5<a<6”.故本题答案选D.
所以2a+1≥3且3a-3≤18,且3a-3≥2a+1,解得4≤a≤7.综合四个选项,只有“5<a<6”能推出“A∩B=A”,而由“A∩B=A”推不出“5<a<6”.故本题答案选D.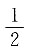
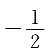
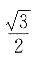
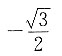
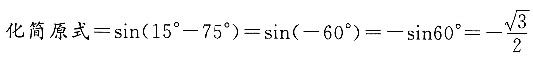 ,因此本题选D.
,因此本题选D. (θ为参数)所表示的曲线为______.
(θ为参数)所表示的曲线为______.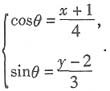 又因为cos2θ+sin2θ=1,则
又因为cos2θ+sin2θ=1,则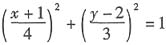 ,即
,即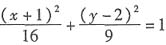 ,表示的是椭圆.如对各种圆锥曲线的参数方程非常熟悉,也可直接判断.
,表示的是椭圆.如对各种圆锥曲线的参数方程非常熟悉,也可直接判断.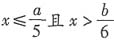 .又因为(A∩B)∩N={2,3,4},所以
.又因为(A∩B)∩N={2,3,4},所以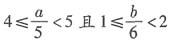 ,即20≤a<25,6≤b<12,a有5种取值,b有6种取值,所以整数对(a,b)的个数为6×5=30.
,即20≤a<25,6≤b<12,a有5种取值,b有6种取值,所以整数对(a,b)的个数为6×5=30.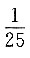

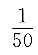
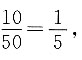 老师两次叫学生发言的事件相互独立,所以概率为
老师两次叫学生发言的事件相互独立,所以概率为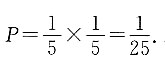 本题应注意老师两次叫的学生可能为同一人.
本题应注意老师两次叫的学生可能为同一人.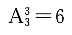 种排法,再将“+”,“-”两个符号插入,中间两个空中有
种排法,再将“+”,“-”两个符号插入,中间两个空中有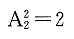 种方法,共有6×2=12种方法,选B.
种方法,共有6×2=12种方法,选B. 若f(2-x2)>f(x),则实数x的取值范围是______
若f(2-x2)>f(x),则实数x的取值范围是______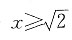 时,2-x2≤0,有(2-x2)3>ln(x+1),此时因为(2-x2)3≤0,ln(x+1)>0,所以不等式无解;当
时,2-x2≤0,有(2-x2)3>ln(x+1),此时因为(2-x2)3≤0,ln(x+1)>0,所以不等式无解;当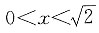 时,2-x2>0,有ln(2-x2+1)>ln(x+1),等价于
时,2-x2>0,有ln(2-x2+1)>ln(x+1),等价于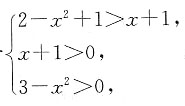 解得-1<x<1,结合前提条件得0<x<1;当
解得-1<x<1,结合前提条件得0<x<1;当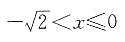 时,2-x2>0,有ln(2-x2+1)>x3,此时因为ln(2-x2+1)=ln(3-x2)>ln 1=0,x3≤0,不等式恒成立,故有
时,2-x2>0,有ln(2-x2+1)>x3,此时因为ln(2-x2+1)=ln(3-x2)>ln 1=0,x3≤0,不等式恒成立,故有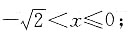 当
当 时,2-x2≤0,有(2-x2)3>x3,即2-x2>x,解得-2<x<1,结合前提条件得
时,2-x2≤0,有(2-x2)3>x3,即2-x2>x,解得-2<x<1,结合前提条件得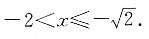 综上,得-2<x<1.
综上,得-2<x<1.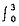 (1+2x)dx,a2=5,则S3为______.
(1+2x)dx,a2=5,则S3为______.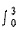 (1+2x)dx=(x+x2)
(1+2x)dx=(x+x2)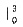 =12,d=a2-a1=5-12=-7,则a3=a2+d=5-7=-2,S3=12+5-2=15.
=12,d=a2-a1=5-12=-7,则a3=a2+d=5-7=-2,S3=12+5-2=15.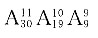
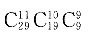
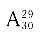
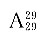
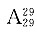 种,班主任插在第一排中间,不影响排列结果.
种,班主任插在第一排中间,不影响排列结果.

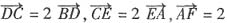
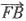 ,则
,则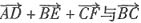 ______.
______.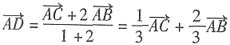 ,同理得
,同理得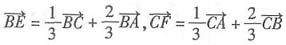 ,以上三式相加得
,以上三式相加得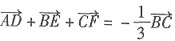 ,所以选A.
,所以选A.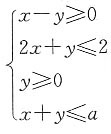 表示的平面区域是一个三角形,则a的取值范围是______
表示的平面区域是一个三角形,则a的取值范围是______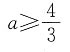
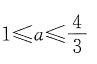
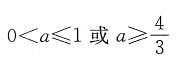
 表示的平面区域如图所示(阴影部分).解
表示的平面区域如图所示(阴影部分).解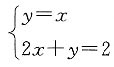 得
得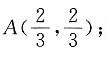 解
解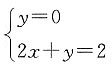 得B(1,0).若原不等式组表示的平面区域是一个三角形,则直线x+y=a中的a的取值范围是0<a≤1或
得B(1,0).若原不等式组表示的平面区域是一个三角形,则直线x+y=a中的a的取值范围是0<a≤1或
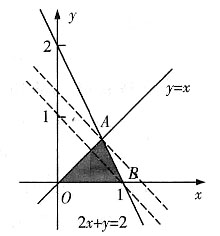
 ”如下,对任意的m=(a,b),n=(c,d),令
”如下,对任意的m=(a,b),n=(c,d),令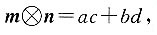 则下列说法错误的是______.
则下列说法错误的是______.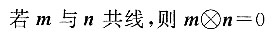
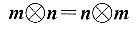
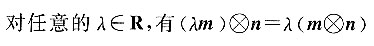
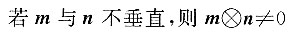
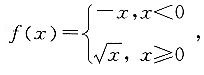 则下列说法正确的是______.
则下列说法正确的是______.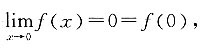 故f(x)连续,又因为
故f(x)连续,又因为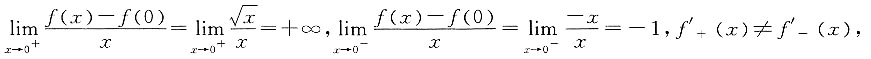 因此f(x)导数不存在,又因为y=f(x)在点(0,0)处存在切线x=0,故C项正确.
因此f(x)导数不存在,又因为y=f(x)在点(0,0)处存在切线x=0,故C项正确.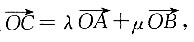 其中λ+μ=1,则点C的轨迹方程是______.
其中λ+μ=1,则点C的轨迹方程是______. 即3x+2y-7=0.
即3x+2y-7=0.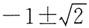
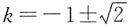 .
.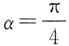 时,S取最大值32π,此时球的表面积与该圆柱的侧面积之差为32π.
时,S取最大值32π,此时球的表面积与该圆柱的侧面积之差为32π.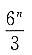
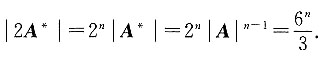
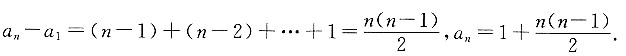 当n=12时,a12=67.
当n=12时,a12=67.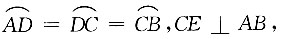 垂足为E,与BD交于F,已知
垂足为E,与BD交于F,已知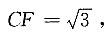 则⊙O的直径为______.
则⊙O的直径为______.
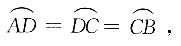 所以∠COB=∠DOA=60°,∠ABD=30°,因为CE⊥AB,OB=OC=r,所以
所以∠COB=∠DOA=60°,∠ABD=30°,因为CE⊥AB,OB=OC=r,所以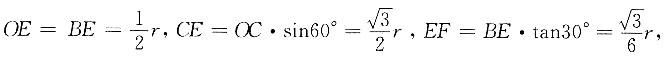 所以
所以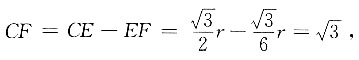 故r=3,直径d=2r=6.
故r=3,直径d=2r=6.

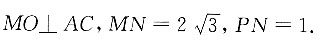 因为△PON∽△PGC,所以
因为△PON∽△PGC,所以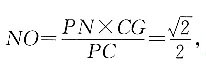 所以
所以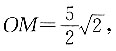 S△ACM=10.
S△ACM=10.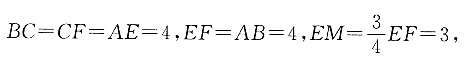
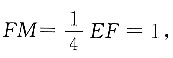 在Rt△AEM、Rt△MFC、Rt△ABC中,
在Rt△AEM、Rt△MFC、Rt△ABC中,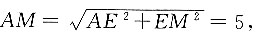
 利用余弦定理,
利用余弦定理,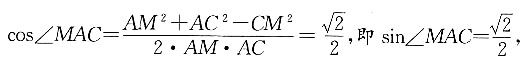
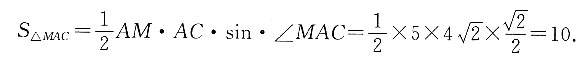

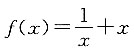 在定义域(1,+∞)上的单调性.
在定义域(1,+∞)上的单调性.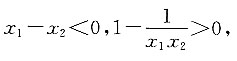
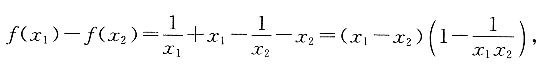 所以f(x1)-f(x2)<0,
所以f(x1)-f(x2)<0,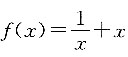 ,在定义域(1,+∞)上单调递增.
,在定义域(1,+∞)上单调递增.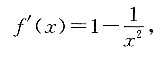
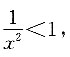
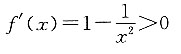
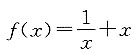 在定义域(1,+∞)上单调递增.
在定义域(1,+∞)上单调递增.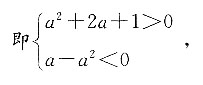

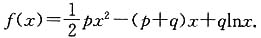 (其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(n,2Sn)(n∈N+)均在函数
(其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(n,2Sn)(n∈N+)均在函数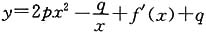 的图象上,(其中f'(x)是函数f(x)的导函数).
的图象上,(其中f'(x)是函数f(x)的导函数).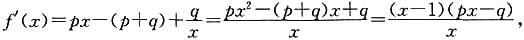


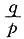
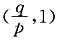

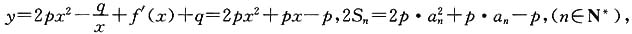
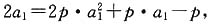 得p=1.
得p=1.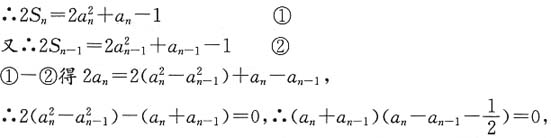
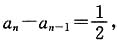 所以{an}是以a1=1,公差为
所以{an}是以a1=1,公差为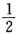 的等差数列,
的等差数列,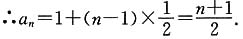
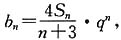 求数列{bn}的前n项和Tn.
求数列{bn}的前n项和Tn.