一、单项选择题4. 已知x
1,x
2,…,x
20的平均数是a;x
21,x
22,…,x
30的平均数是b,则x
1,x
2…x
30的平均数是______.
A.
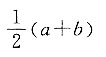
B.
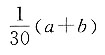
C.
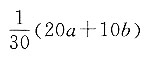
D.
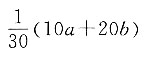
A B C D
C
[解析] 依题意得,x
1+x
2+…+x
20=20a,x
21+x
22+…+x
30=10b,所以x
1+x
2+…+x
30=20a+10b,
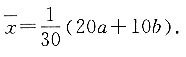
8. 分段函数
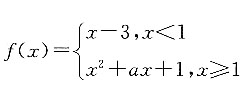
的值域为R,则a的值可能是______.
A B C D
D
[解析] x<1时,函数的值域为(-∞,-2);x≥1时,
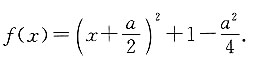
分两种情况进行讨论:①当a>0时,
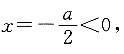
即f(x)的对称轴在x轴的负半轴,此时当x=1时,f(x)有最小值,因为函数的值域为R,故应有f(1)=1+a+1≤-2,得a≤-4,故此时a无解;②当a<0时,
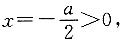
此时
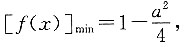
因为值域为R,所以
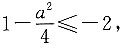
解得
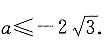
四个选项中只有D项符合条件.
12. 如图所示,一小船在离岸边12米处由岸上拉索拉靠岸.已知岸高5米,当拉索向前进了5米时,小船向前行驶了______米.
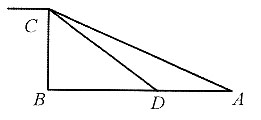
A.
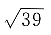
B.7
C.
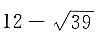
D.5
A B C D
C
[解析] 设小船在A地时,距离岸边B为12米,岸高BC=5米,所以拉索
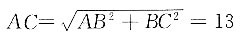
米;当拉索向前进了5米时,小船行驶到D地,此时CD=13-5=8米,所以
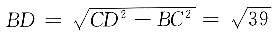
米,则小船前进了
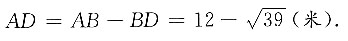
13. 若两圆周长之比为9:4,则两圆面积之比为______.
A B C D
D
[解析] 圆的周长C=2πr,面积S=πr
2.因为C
1:C
2=9:4,所以r
1:r
2=9:4,则
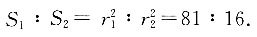
14. 已知复数
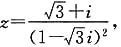
则
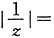
______.
A.
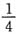
B.
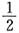
C.1
D.2
A B C D
D
[解析] 因为
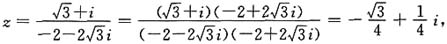
所以
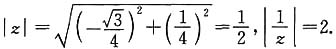
故选D.
16. 设a
0为单位向量,①若a为平面内的某个向量,则a=|a|a
0;②若a与a
0平行,则a=|a|a
0;③若a与a
0平行且|a|=1,则a=a
0.上述命题中,假命题的个数是______
A B C D
D
[解析] 向量是既有大小又有方向的量,a与|a|a0的模相等,但方向不一定相同,故①是假命题;若a与a0平行,则a与a0的方向有两种情况:一是同向,二是反向,反向时a=-|a|a0,故②③也是假命题.综上所述,假命题的个数是3.
19. 设曲线
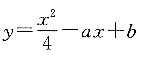
和y=xy
3+1在点(2,-1)处相切,其中a、b是常数,则______.
A.a=0,b=2
B.

C.
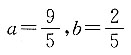
D.
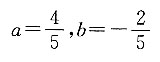
A B C D
D
[解析] 由已知可得,曲线
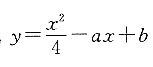
在点(2,-1)处的斜率

将方程y=xy
3+1对x求导得y'=y
3+3xy
2y',则该曲线在(2,-1)处的斜率y'(2)=(-1)
3+3×2×(-1)
2y'(2),
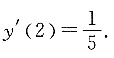
因为这两条曲线在(2,-1)处相切,所以在该点它们的斜率相同,即
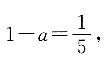
解得
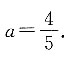
又因为曲线
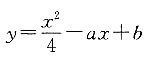
过点(2,-1),即
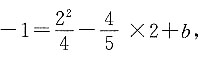
所以
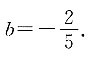
20. 设全集U=R,集合M={x|x
2>1},N={x|x>-3},下列关系中正确的是______.
A.
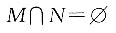
B.M∩N=N
C.M∪N=R
D.M∪N=M
A B C D
C
[解析] 因为M={x>1或x<-1},所以M∩N={x|-3<x<-1或x>1},M∪N=R,所以本题选C.
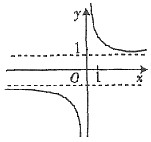
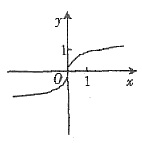
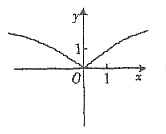
23. 函数
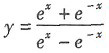
的图象大致为______.
A.
B.

C.
D.
A B C D
A
[解析]

则
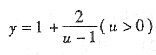
在[0,1)上递减,在(1,+∞)上递减,而u=e
2x在R上递增.∴
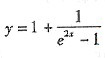
的单调区间都是减的.故选A.
24. 设命题p:1≤x≤5;命题q:x
2-ax+2≤0.命题p是命题q的充分不必要条件,则a的取值范围为______.
A.
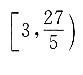
B.(-∞,3]
C.[3,+∞)
D.
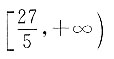
A B C D
D
[解析] 因为命题p是命题q的充分不必要条件,所以由p可以推出q,由q不能推出p,则不等式x
2-ax+2≤0的解集不为空集.命题q:x
2-ax+2≤0,即

则
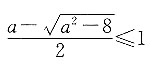
且
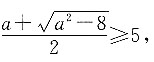
解得
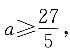
所以a的取值范围为
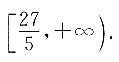
26. 函数y=f(2x-1)的定义域为(0,3),则f(x
2+1)的定义域为______.
A.(1,5)
B.
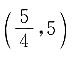
C.(1,10)
D.
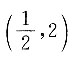
A B C D
B
[解析] y=f(2x-1)的定义域为(0,3),即0<2x-1<3,解得
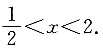
则
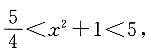
即f(x
2+1)的定义域为
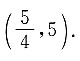
27. 下列数与
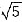
相差最小的是_______
A.2
B.
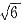
C.
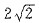
D.3
A B C D
B
[解析]本题主要考查无理数的大小判断.
四个选项可分别转化为
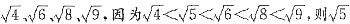
与哪个数之差最小的问题,只需比较
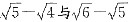
的大小即可.
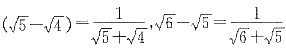
,因为
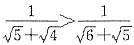
,故
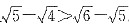
.即四个数字中
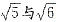
相差最小.
二、填空题1. 数形结合的思想,其实质是将抽象的数学语言和______结合起来,使代数问题几何化、几何问题代数化.
直观的图象
[解析] 数形结合的关键是代数问题和图形之间的互相转化,将抽象的数学语言和直观的图象结合起来,使问题获得解决.
2. (x+1)
9的展开式中x
3的系数是______.(用数字作答)
84
[解析] (x+1)
9的展开式中x
3的系数是

.
3. 已知对数函数f(x)=lg(x
2+1)-1,则f[f(0)]=______.
-lg5
[解析] f(0)=lg1-1=-1,则f[f(0)]=f(-1)=lg2-1=-lg5.
4. 若函数
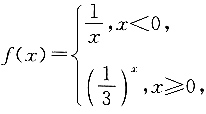
则不等式
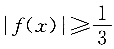
的解集为______.
[-3,1]
[解析] 依题可得
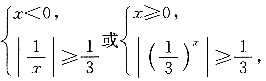
解之得-3≤x<0或0≤x≤1,所以不等式
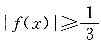
的解集为[-3,1].
5. 数字表诗各字如下:
| 白 | 日 | 依 | 山 | 尽 | , | 黄 | 河 | 入 | 海 | 流 | ; |
| 1 | 2 | 3 | 4 | 5 | | 6 | 7 | 8 | 9 | 10 | |
| 欲 | 穷 | 千 | 里 | 目 | , | 更 | 上 | 一 | 层 | 楼 | ; |
| 11 | 12 | 13 | 14 | 15 | | 16 | 17 | 18 | 19 | 20 | |
若以此中四个数组成一个成语,成语中第一个字对应的数字是第二个字对应的数字的9倍,第四个字对应的数比第三个字对应的数大2,第二个字对应的数为第四个字对应数字的
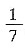
,则这个成语是______.
6. 若直线x-2y+5=0与直线2x+my-6=0互相垂直,则实数m=______.
1
[解析] 因为直线x-2y+5=0与直线2x+my-6=0互相垂直,所以(1,-2)(2,m)=2-2m=0,m=1.
7. 若向量
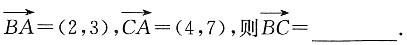
(-2,-4)
[解析]
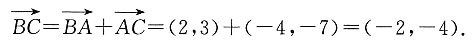
8. 数学教学基本功包括______、语言表达的技能、组织和调控课堂的技能、______。
9. 已知数列{a
n}为公比大于1的等比数列,且满足9a
3-a
5=0,则
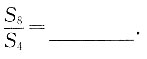
82
[解析] 已知数列{a
n}为等比数列,则9a
3-a
5=9×a
1q
2-a
1q
4=0,因为数列{a
n}公比大于1,所以

10. ______是学生将所学的数学知识转化为数学技能、技巧,形成数学能力的重要途径和手段.
数学练习
[解析] 数学练习是一种有目的、有组织、有指导的数学学习实践活动,是学生将所学的数学知识转化为数学技能、技巧,形成数学能力的重要途径和手段.通过练习可以使学生从不会到会,从不熟练到熟练.
三、解答题已知a,b,c分别为△ABc三个内角A,B,c的对边,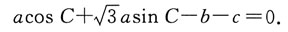
1. 求A;
由
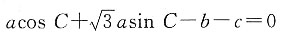
及正弦定理得
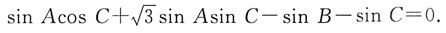
因为B=π-A-C,所以sin B=sin(A+C)=sin Acos C+cos Asin C,
所以
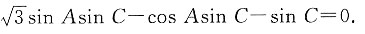
由于sin C≠0,所以
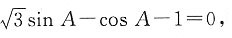
即
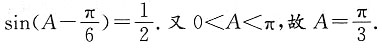
2. 若n=2,△ABC的面积为
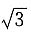
,求b,c.
△ABC的面积
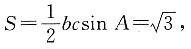
故bc=4.
而a
2=b
2+c
2-2bccos A,故b
2+c
2=8.解得b=c=2.
3. 在数学教学中,如何贯彻严谨性与量力性相结合的原则?
教师认真了解学生的心理特点与接受能力。教学过程中,严谨性的要求应是明确的、积极的和逐步提高的,要求学生语言精确、思考缜密、言必有据、思路清晰。教师的每一节课都应力争结构、层次和步骤都有条不紊;在具体的解题过程中,要做到步骤清晰。
4. 简述运用问题探索法进行教学的一般步骤.
(1)创造探索条件.学生能顺利地进行探索,需要有一定的条件,就是要围绕探索新问题而选择的必备知识和经验,它起着承前启后的桥梁作用.可通过学生回答问题或进行课堂练习为探索新问题创造条件.
(2)引出探索问题和结论.教师要注意向学生指明探索途径,使学生思维朝着正确方向发展,形成新的认识过程,找出推理依据,并做出评价.
(3)总结探索成果.通过探索得到结论后,还须回顾探索过程,找出思维规律,将获得的知识、技能同提高能力统一起来,达到获得知识,发展能力,促进全面发展的目的.
5. 甲、乙二位同学同时开始数棋子,甲数7个时,乙数5个,现乙数至55个时,忘记了自己所数的数,又从1开始继续数其余的棋子,数至135个时,棋子数完了,求棋子的总数.
解:设甲数棋子的速度是7x,乙数棋子的速度是5x,棋子总数为y,则有:
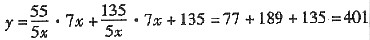
.
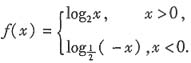 若f(a)>f(-a),则实数a的取值范围是______.
若f(a)>f(-a),则实数a的取值范围是______.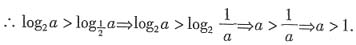
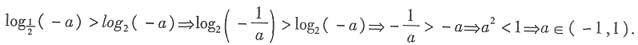
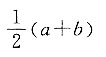
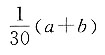
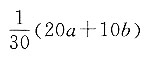
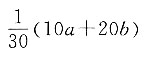
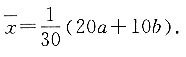
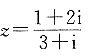 (i是虚数单位)在复平面对应的点位于______.
(i是虚数单位)在复平面对应的点位于______.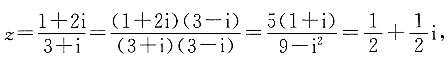 因此z在复平面上对应的点位于第一象限.
因此z在复平面上对应的点位于第一象限.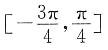
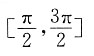
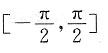
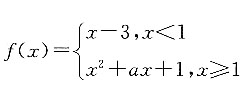 的值域为R,则a的值可能是______.
的值域为R,则a的值可能是______.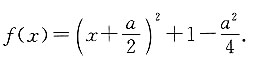 分两种情况进行讨论:①当a>0时,
分两种情况进行讨论:①当a>0时,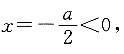 即f(x)的对称轴在x轴的负半轴,此时当x=1时,f(x)有最小值,因为函数的值域为R,故应有f(1)=1+a+1≤-2,得a≤-4,故此时a无解;②当a<0时,
即f(x)的对称轴在x轴的负半轴,此时当x=1时,f(x)有最小值,因为函数的值域为R,故应有f(1)=1+a+1≤-2,得a≤-4,故此时a无解;②当a<0时,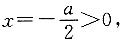 此时
此时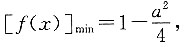 因为值域为R,所以
因为值域为R,所以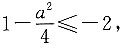 解得
解得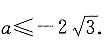 四个选项中只有D项符合条件.
四个选项中只有D项符合条件.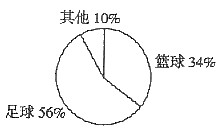
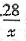 =56%,解得,x=50.
=56%,解得,x=50.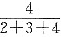 =80°,故为锐角三角形,选B.
=80°,故为锐角三角形,选B.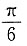 ,且与平面α,β分别相交于点A,B,点S∈l,AS=5,BS=1,则平面α,β之间的距离是______
,且与平面α,β分别相交于点A,B,点S∈l,AS=5,BS=1,则平面α,β之间的距离是______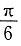 ,得此时平面α,β之间的距离是2;当点S在平面α,β之间时,AB=6,同理得平面α,β之间的距离是3,故选择C.
,得此时平面α,β之间的距离是2;当点S在平面α,β之间时,AB=6,同理得平面α,β之间的距离是3,故选择C.
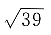
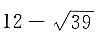
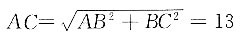 米;当拉索向前进了5米时,小船行驶到D地,此时CD=13-5=8米,所以
米;当拉索向前进了5米时,小船行驶到D地,此时CD=13-5=8米,所以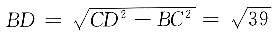 米,则小船前进了
米,则小船前进了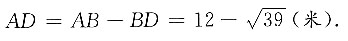
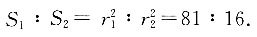
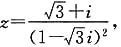 则
则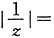 ______.
______.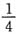
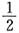
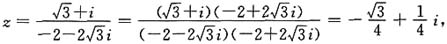 所以
所以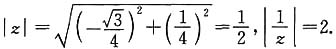 故选D.
故选D.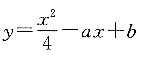 和y=xy3+1在点(2,-1)处相切,其中a、b是常数,则______.
和y=xy3+1在点(2,-1)处相切,其中a、b是常数,则______.
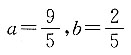
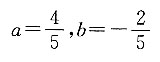
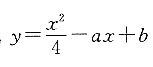 在点(2,-1)处的斜率
在点(2,-1)处的斜率 将方程y=xy3+1对x求导得y'=y3+3xy2y',则该曲线在(2,-1)处的斜率y'(2)=(-1)3+3×2×(-1)2y'(2),
将方程y=xy3+1对x求导得y'=y3+3xy2y',则该曲线在(2,-1)处的斜率y'(2)=(-1)3+3×2×(-1)2y'(2),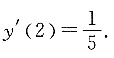 因为这两条曲线在(2,-1)处相切,所以在该点它们的斜率相同,即
因为这两条曲线在(2,-1)处相切,所以在该点它们的斜率相同,即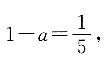 解得
解得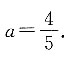 又因为曲线
又因为曲线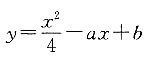 过点(2,-1),即
过点(2,-1),即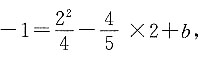 所以
所以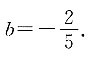
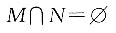
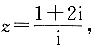 则复数
则复数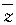 =______.
=______.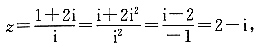 则
则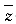 =2+i
=2+i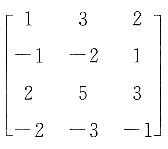 的秩为______.
的秩为______. ,所以矩阵的秩为3.
,所以矩阵的秩为3.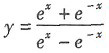 的图象大致为______.
的图象大致为______.



 则
则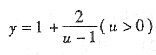 在[0,1)上递减,在(1,+∞)上递减,而u=e2x在R上递增.∴
在[0,1)上递减,在(1,+∞)上递减,而u=e2x在R上递增.∴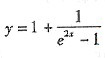 的单调区间都是减的.故选A.
的单调区间都是减的.故选A.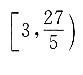
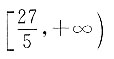
 则
则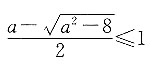 且
且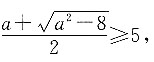 解得
解得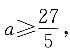 所以a的取值范围为
所以a的取值范围为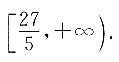
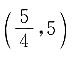
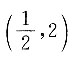
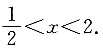 则
则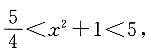 即f(x2+1)的定义域为
即f(x2+1)的定义域为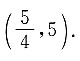
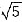 相差最小的是_______
相差最小的是_______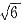
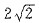
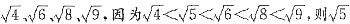 与哪个数之差最小的问题,只需比较
与哪个数之差最小的问题,只需比较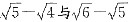 的大小即可.
的大小即可.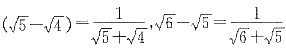 ,因为
,因为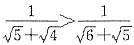 ,故
,故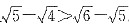 .即四个数字中
.即四个数字中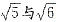 相差最小.
相差最小. .
.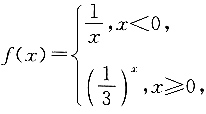 则不等式
则不等式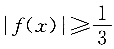 的解集为______.
的解集为______.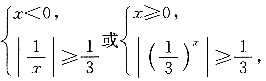
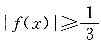 的解集为[-3,1].
的解集为[-3,1].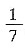 ,则这个成语是______.
,则这个成语是______.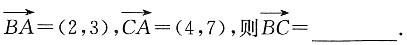
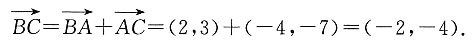


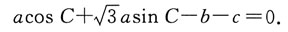
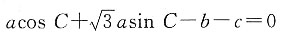 及正弦定理得
及正弦定理得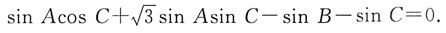
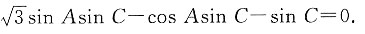
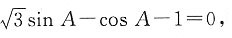 即
即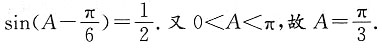
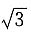 ,求b,c.
,求b,c.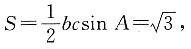 故bc=4.
故bc=4.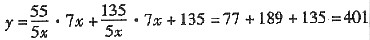 .
.