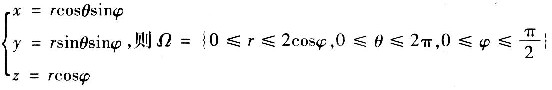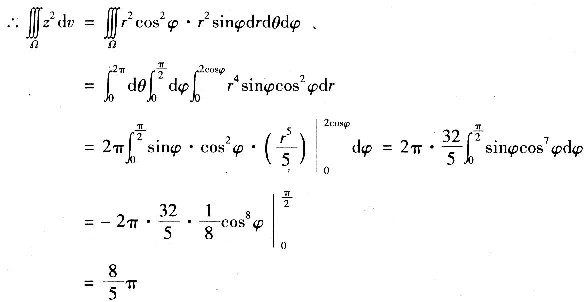二、填空题1. 设函数
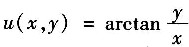
,则
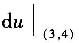
=______.
2. 设z=f(x
6-y
6)可微,则
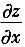
=______.
3. 三重积分
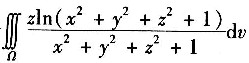
=______,其中Ω是球x
2+y
2+z
2≤1.
0
因为Ω关于平面z对称,
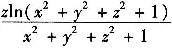
为z的奇函数
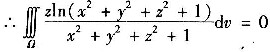
4. 微分方程y"+4y'+3y=0的通解为y=______.
c1e-x+c2e-3x
∵特征方程为r2+4r+3=0∴r1=-3,r2=-1,从而通解为y=c1e-x+c2e-3x
5. 幂级数
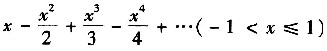
的和函数是______.
ln(1+x)
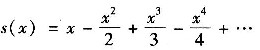
令
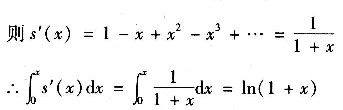
即s(x)-s(0)= ln(1+x)显然s(0)=0∴s(x)=ln(1+x)
三、计算题1. 已知向量a={1,0,-2},b={1,1,0},试求向量c,使c⊥a,c⊥b且|c|=6.
设c={x,y,z}
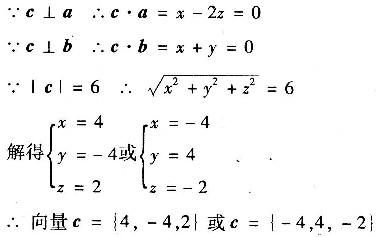
2. 讨论函数
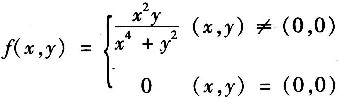
在点(0,0)处的连续性.
令y=kx
2,则
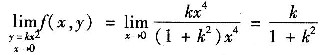
上述极限随k的不同而不同.
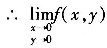
不存在
∴f(x,y)在(0,0)点不连续.
3. 求函数u=f(x,y,z)=x
2+xy+yz在点(1,0,3)处沿方向角为α=60°,β=45°,r=60°的方向导数.
4. 令z=x
y,而x=sint,y=cost,求
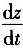
.
5. 求出z=x
3+y
3-3xy的极值.
f(x,y)=x
3+y
3-3xy
∴f
x(x,y)=3x
2-3y,f
y(x,y)=3y
2-3x
A=f
xx=6x,B=f
xy=-3,c=f
yy=6y
令
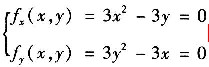
得驻点(1,1)(0,0)
关于第一个驻点(1,1)有B
2-AC=9-6×6=-27<0且A>0
因此(x,y)在点(1,1)取得极小值f(1,1)=1+1-3=-1
关于第二个驻点(0,0)有B
2-AC=9>0,因此f(x,y)在(0,0)点取不到极值.
6. 计算二重积分
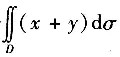
,其中D:x
2+y2≤x+y+1.
7. 求心形线r=a(1+cosθ)的长度.
由于
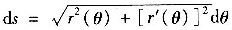
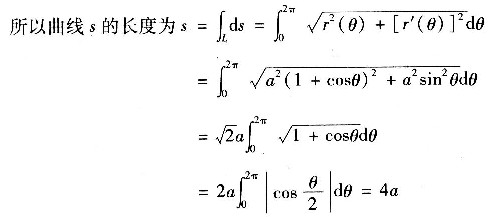
8. 计算
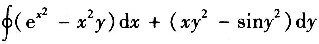
,L是圆周x
2+y
2=a
2沿逆时针方向.
9. 计算
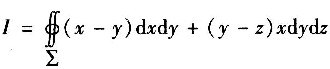
,∑为柱面x
2+y
2=1及平面z=0,z=3所围成立体的全表面外侧.
P=(y-z)x,Q=0,R=x-y
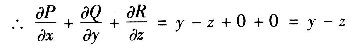
设封闭曲面所围的空间区域为Ω,利用高斯公式和柱面坐标有
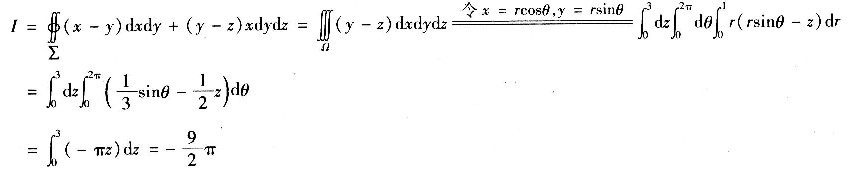
10. 判断正项级数
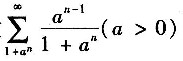
的敛散性.
11. 求幂级数
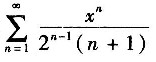
的收敛半径和收敛区间.
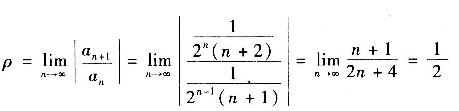
∴级数的收敛半径为

对x=2,原级数成为
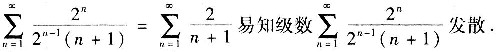
对x=-2,原级数成为
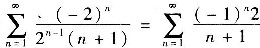
是交错级数,由莱布尼茨判别法知该级数收敛.
∴级数
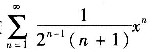
的收敛半径为2,收敛区间是[-2.2)
12. 求微分方程y"+3y'+2y=e
-x.
对应齐次方程的特征方程为r2+3r+2=0
∴r1=-2,r2=-1
∴齐次方程的通解为y=C1e-2x+C2e-x
∵r2=-1是特征方程的单根
∴应设特解为y*=Axe-x
则 y*'=Ae-x-Axe-x,y*"=-Ae-x-Ae-x+Axe-x=-2Ae-x+Axe-x,
将它们代入原方程得
(-2Ae-x+Axe-x)+3(Ae-x-Axe-x)+2Axe-x=e-x
∴Ae-x=e-x ∴A=1
所以原方程的一个特解y*=xe-x
于是原方程的通解为y=c1e-2x+c2e-x+xe-x
四、综合题1. 将函数
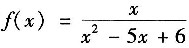
展开成关于x-5的幂级数.
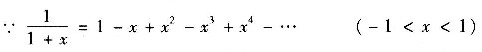
令t=x-5,则
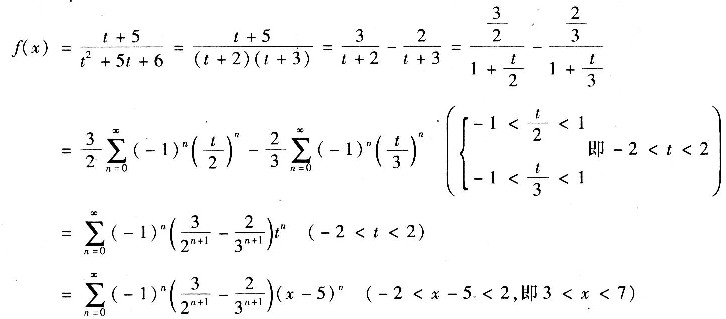
2. 计算曲线积分为
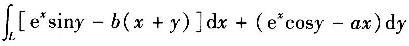
,其中a,b均为正常数.L是从点A(2a,0)沿曲线
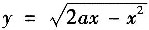
到原点的弧度.(如图)
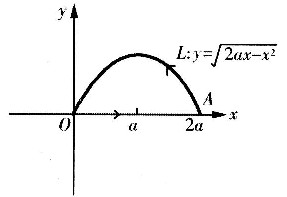
3. 设Ω是球体x
2+y
2+z
2≤2z,求三重积分
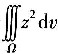
.
令