二、填空题1. 二重极限
=______．
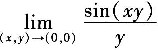
2. 二重积分
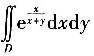
=______，其中D={(x，y)|x
2+y
2≤1}，常数a，b＞0．
3. 设二元函数
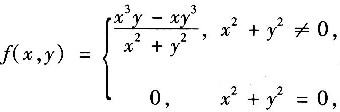
则f
xy(0，0)=______．
-1
当
，并且
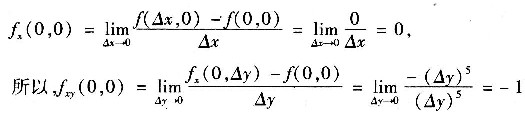
4. 极限
=______．
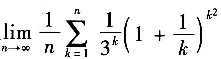
0
考虑级数
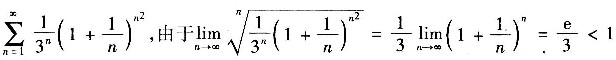
所以，这一正项级数收敛，因此
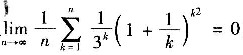
5. 设函数y=e
2x+(x+1)e
x是二阶常系数线性微分方程y"+ay'+by=ce
x的一个特解，则常数a，b，c及该微分方程的通解为______．
a=-3，b=2，c=-1，y=C1ex+C2e2x+xex
将y=e
2x+x+1)e
x代入y"+ay'+by=ce
x得：
(4+2a+v)e
2x+a[2e
2x+(x+2)e
x]+b[e
2x+(x+1)e
x]=xe
x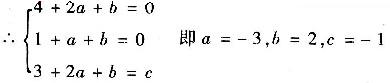 
∴该方程为y"-3y'+2y=-e
x 对应的齐次特征方程r
2-3r+2=0的根为r=1，2，所以通解y=c
1e
x+c
2e
2x ∴y"-3y'+2y=-e
x的通解为y=c
1e
x+c
2e
2x+[e
2x+(x+1)e
x]=C
1e
x+C
2e
2x+xe
x)
三、计算题1. 从点A
3，-2，4)沿a={2，-10，11}的方向取长度为45的线段AB，求点B的坐标．
设点B
x，y，z)，则
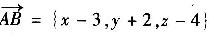
因为
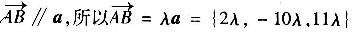
因为
解之得λ=3，所以
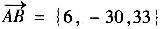
由x-3=6，y+2=-30，z-4=33得，所求点B的坐标是(9，-32，37)
2. 求曲面S：(x-y)
2-z
2=1在点M(1，0，0)的切平面π的方程．
设F(x，y，z)=(z-y)2-z2-1，则
所以s在点M处的切平面百的方程为2(x-1)-2y=0，即x-y-1=0
3. 求函数u=xyz在点(5，1，2)处，沿A(5，1，2)到B(9，4，14)的方向l的方向导数．
4. 设二元函数z=z(x，y)由方程z=x+ye
z确定，求
．
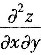
所给方程两边分别关于x，y求偏导数，得
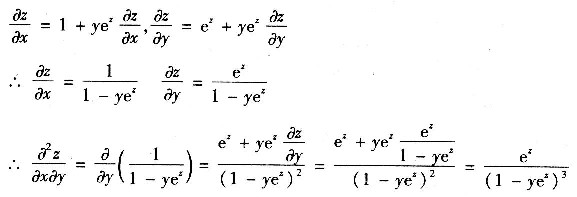
5. 求函数z=x
2+y
2在
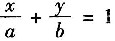
条件下的极值．
6. 设B是由
，y=x和x=2所围成的平面区域，求二重积分
．
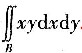
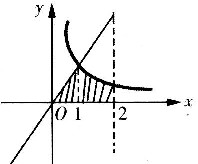
积分区域如图所示
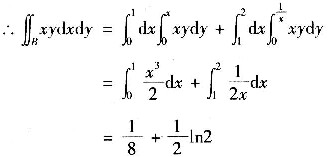
7. 设L为椭圆争
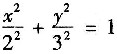
，其周长为l，计算曲线积分
．
由于积分路线L关于x=0对称，函数xy
2关于x为奇函数，故
又沿曲线
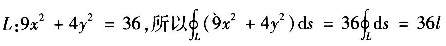
于是所求曲线积分
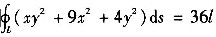
8. 计算
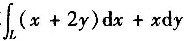
，其中L是从点(0，1)沿曲线
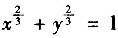
(x≥0)到点(1，0)．
L的参数方程为
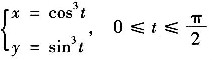
故
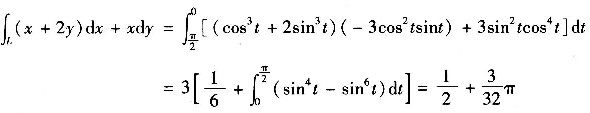
9. 计算
，其中∑是立体
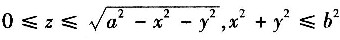
(a＞b＞0)的表面的外侧．
11. 把f(x)=ln(1+x+x
3)展开为x的幂级数．
12. 求微分方程y"=y'+x的解．
令y'=p，则
，代入方程得
为一阶线性微分方程，解得p=c
1e
x-x-1，即：y'=c
1e
x-x-1，积分得
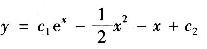
四、综合题1. 指出幂级数
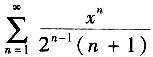
的收敛半径和收敛区间．
2. 求方程e
ydx+(xe
y+2y)dy=0的通解．
P=e
y，Q=xe
y+2y
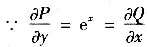
，故存在一个二元函数F(x，y)使
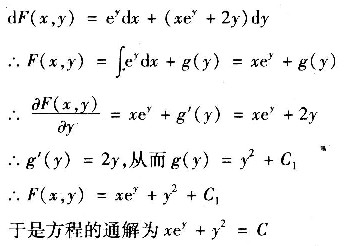
3. 在一长宽高之为和某一常数c的长方体中，求出一个具有最大体积者
设长方体的长、宽、高分别为x，y，z，体积V=xyz，x+y+z=c
构造拉格朗日函数F(x，y，z，λ)=xyz-λ(x+y+z-c)
令
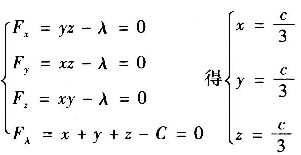
根据实际意义知
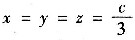
时，体积最大．
D．-y2
，则 
存在表明其对应的P(x，y)→P0(x0，y0)的路径为二重极限
的P→P0各种路径中的一条，所以，
收敛，则下列级数中收敛的为 
为 
D．
的敛散性．
深色：已答题 浅色：未答题