银符考试题库B12
现在是：
试卷总分：100.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
河北省专升本高等数学(二)真题汇编1
一、单项选择题
(在每小题给出的四个备选项中，选出一个正确的答案)
1.
的定义域为______
A.(2，+∞)
B.[2，+∞)
C.(1，2)
D.(-∞，1]
A
B
C
D
B
[解析] 由
解得x≥2，故选B．
2. 下列等式正确的是______
A．
B．
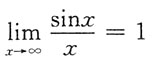
C．
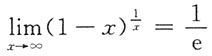
D．
A
B
C
D
A
[解析] A项，
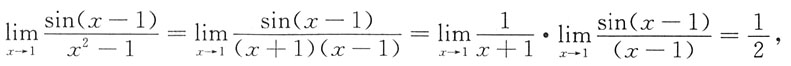
A正确；B项，由于|sinx|≤1，而
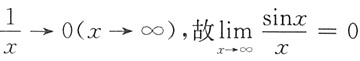
，B错误；
C项，
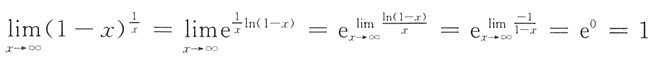
，C错误；
D项，
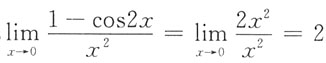
．D错误．
3.
，则x=0是f(x)的______
A.可去间断点
B.跳跃间断点
C.第二类间断点
D.连续点
A
B
C
D
B
[解析]
，
，
，故x=0是f(x)的跳跃间断点．
4. 设f(x)=1-x，
，则当x→1时______
A.f(x)是比g(x)高阶的无穷小
B.f(x)是比g(x)低阶的无穷小
C.f(x)与g(x)是同阶但不等价的无穷小
D.f(x)与g(x)是等价无穷小
A
B
C
D
C
[解析]
，故当x→1时，f(x)与g(x)是同阶但不等价的无穷小．
5. 由方程e
y
+ln(x+y)=x所确定的隐函数y=f(x)的导数
______
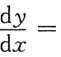
A．
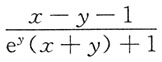
B．
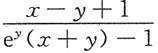
C．
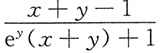
D．
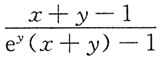
A
B
C
D
C
[解析] 方程两边同时对x求导，可得
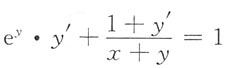
，整理可得
6. z=e
u
sinv，而u=xy，v=x+y，
______
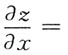
A.
exy
[ysin(x+y)+cos(x+y)]
B.e
xy
[xsin(x+y)-cos(x+y)]
C.e
xy
[ysin(x+y)-cos(x+y)]
D.e
xy
[xsin(x+y)+cos(x+y)]
A
B
C
D
A
[解析]
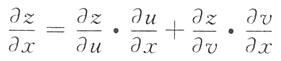
=e
u
·sinv·y+e
u
cosv
=e
xy
[ysin(x+y)+cos(x+y)]．
7. 极限
______
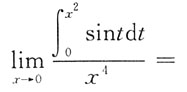
A．
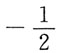
B．-1
C．1
D．
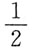
A
B
C
D
D
[解析]
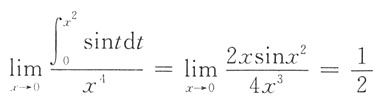
，故选D．
8. 已知矩阵
，则r(A)=______
A.0
B.1
C.2
D.3
A
B
C
D
C
[解析] 对A进行初等行变换，
所以r(A)=2．
9. 下列无穷级数中，发散的是______
A．
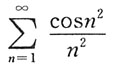
B．
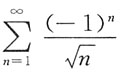
C．
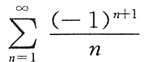
D．
A
B
C
D
D
[解析] A项，由
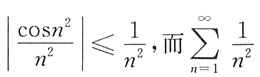
收敛，可知其收敛；B、C项，级数为交错级数，由莱布尼茨判别法可知其收敛；D项，由
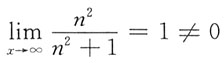
，可知其发散．
10. 幂级数
的收敛半径为______
A.1
B.2
C.4
D.-6
A
B
C
D
B
[解析] 级数的收敛半径
，故选B．
二、填空题
1. 曲线f(x)=x
3
-2x
2
+1，则拐点坐标为______．
[解析] f'(x)=3x
2
-4x，f"(x)=6x-4，令f"(x)=0，得
，又
时，f"(x)＜0，
时，f"(x)＞0，故
是其拐点．
2. 参数方程
所确定曲线在
处的切线方程为______．
[解析]
时，
，曲线在
处的切线方程为
，即
3. 设z=e
xy
2
，则其全微分为______．
dz=ye
xy
2
(ydx+2xdy)
[解析]
，故dz=ye
xy2
(ydx+2xdy)．
4.
在x=1处连续，则a=______．
2
[解析]
，
，f(x)在x=1处连续，则有
，得a=2．
5. 设行列式
，则x=______．
2
[解析]
，故x=2．
三、计算题
(每小题10分，共40分，将解答的过程、步骤和答案填写在相应位置上，写在其他位置上)
1. 计算定积分
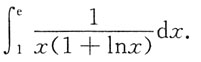
2. 求由曲线y=x
2
，
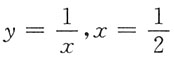
，x=2所围成的平面图形的面积．
曲线y=x
2
，
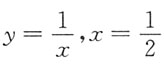
，x=2围成的平面图形如图阴影所示，
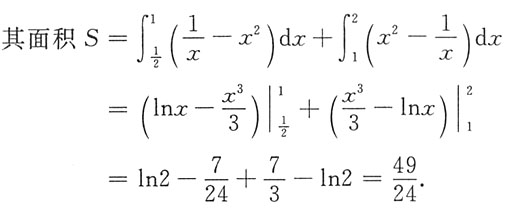
3. 求微分方程
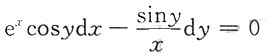
满足初始条件y|
x=0
=0时的特解．
微分方程可化为
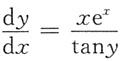
，即xe
x
dx=tanydy，
两边积分可得(x-1)e
x
+C
1
=-ln|cosy|，
又方程满足y|
x=0
=0，代入可得-1+C
1
=0，即C
1
=1，
故所求特解为ln|cosy|=e
x
-xe
x
-1．
4. 已知三阶矩阵
，B=2I，其中I为单位矩阵，AX=B．求矩阵X．
|A|=-2，故A可逆，由AX=B=2I，可得X=2A
-1
，利用初等变换求A
-1
：
四、应用题
(本题10分．将解答的主要过程、步骤和答案填写在相应位置上)
一工厂加工某种产品，固定成本1万元，每多生产一百件产品，成本增加2万元，总收入R(单位：万元)是产量Q(单位：百件)的函数，设需求函数为Q=12-2P．
1. 求利润函数；
由题可知，产量为Q时的成本C=2Q+1，收入
，故利润函数
2. 产量为何值时，利润最大?最大利润是多少?
L'=-Q+4，令L'=0，可得Q=4，又L"=-1＜0，所以当Q=4(百件)时，利润最大，最大利润L(4)=7(万元)；
3. 求当价格P=3时的需求弹性，并解释所得结果的经济含义．
P=3时，Q=6，需求弹性函数为
，故η(3)=1，其经济含义：当P=3时，价格下降百分之一，引起需求量上升百分之一．
一、单项选择题
1
2
3
4
5
6
7
8
9
10
二、填空题
1
2
3
4
5
三、计算题
1
2
3
4
四、应用题
1
2
3
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
的定义域为______
解得x≥2，故选B．
，B错误；
，C错误；
．D错误．
，则x=0是f(x)的______
，
，
，故x=0是f(x)的跳跃间断点．
，则当x→1时______
，故当x→1时，f(x)与g(x)是同阶但不等价的无穷小．
______
，整理可得
______
______
，故选D．
，则r(A)=______
收敛，可知其收敛；B、C项，级数为交错级数，由莱布尼茨判别法可知其收敛；D项，由
，可知其发散．
的收敛半径为______
，故选B．
，又
时，f"(x)＜0，
时，f"(x)＞0，故
是其拐点．
所确定曲线在
处的切线方程为______．
时，
，曲线在
处的切线方程为
，即
，故dz=yexy2(ydx+2xdy)．
在x=1处连续，则a=______．
，
，f(x)在x=1处连续，则有
，得a=2．
，则x=______．
，故x=2．
，x=2所围成的平面图形的面积．
，x=2围成的平面图形如图阴影所示，
满足初始条件y|x=0=0时的特解．
，即xexdx=tanydy，
，B=2I，其中I为单位矩阵，AX=B．求矩阵X．
，故利润函数
，故η(3)=1，其经济含义：当P=3时，价格下降百分之一，引起需求量上升百分之一．
深色：已答题 浅色：未答题