一、单项选择题(在每小题给出的四个备选项中，选出一个正确的答案)4. 已知函数f(x)=x
8+3x
6-2x
5-5x
3+x
2-1，则f
(7)(2)=______
A B C D
D
[解析] f(7)(x)=x·8!，故f(7)(2)=2·8!．
5. 一阶微分方程2xydx+x
2dy=0的通解为______
A．
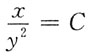
B．
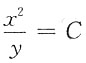
C．x
2y=C
D．xy
2=C
A B C D
C
[解析]
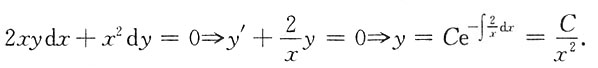
7.
______
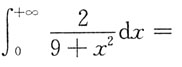
A．
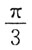
B．
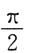
C．
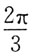
D．π
A B C D
A
[解析]
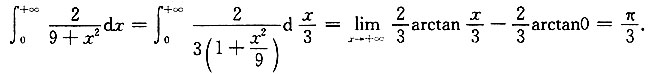
10. 下列无穷级数中，条件收敛的是______
A．
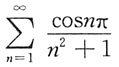
B．
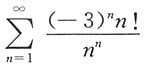
C．
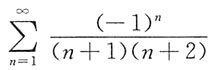
D．
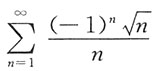
A B C D
D
[解析]
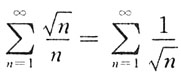
，该级数是
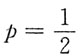
的p
-级数，发散，但
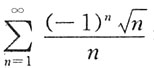
满足莱布尼茨条件，收敛，所以D项级数条件收敛．A、C绝收收敛，B项发散．
二、填空题1. 已知函数z=x
2e
y，则dz=______．
2xeydx+x2eydy
[解析]
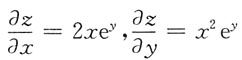
，所以dz=2xe
ydx+x
2e
ydy．
2. 极限
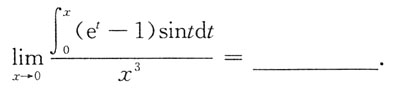
[解析]
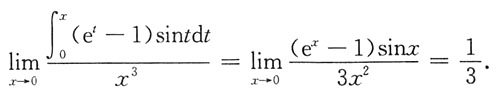
3. 向量组α
1=(1，2，0，1)，α
2=(1，3，0，-1)，α
3=(-1，-1，1，0)的秩为______．
3
[解析]
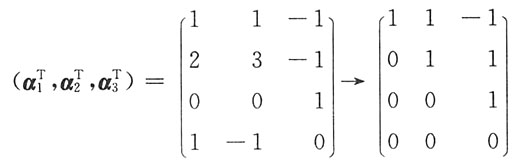
，所以秩为3．
4. 已知函数
在定义域内连续，则a=______，b=______．
[解析] 因为f(x)在定义域内连续，则有
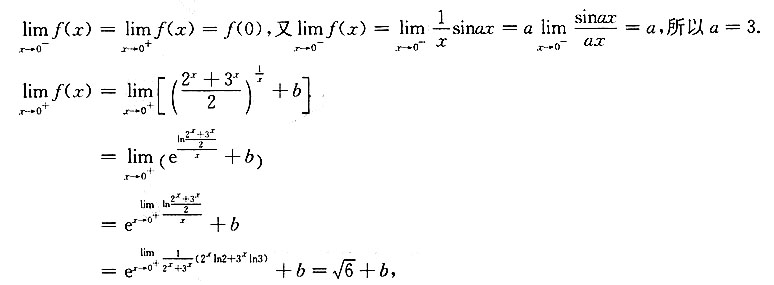
所以
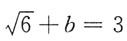
，即
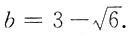
5. 幂级数
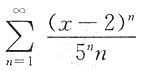
的收敛域为______．
[-3，7)
[解析]
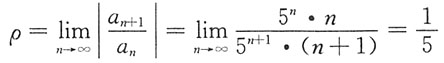
，所以R=5，即-5＜x-2＜5，所以-3＜x＜7．当x=-3时，级数为
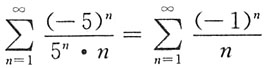
，是交错级数，且满足幕布尼茨条件，收敛；当x=7时，级数为
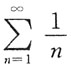
，是调和级数，发散．故该级数收敛域为[-3，7)．
三、计算题(每小题10分，共40分，将解答的主要过程、步骤和答案填写在相应位置上，写在其他位置上无效)1. 设方程xyz=sinxyz确定二元隐函数，z=z(x，y)，求
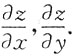
设F(x，y，z)=xyz-sinxyz，
则F
x=yz-yzcosxyz，F
y=xz-xzcosxyz，F
z=xy-xycosxyz．
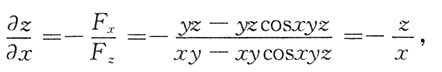
同理可得，
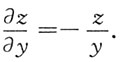
2. 求微分方程y'=2+x+2y
2+xy
2满足初始条件y(0)=1的特解．
原方程化简为y'=(2+x)(1+y
2)，
分离变量得
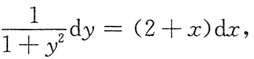
两端积分
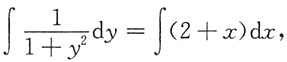
方程的通解为
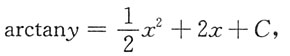
由初始条件y(0)=1，得
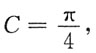
得原方程的特解为
3. 求方程组
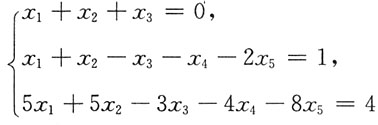
的通解．
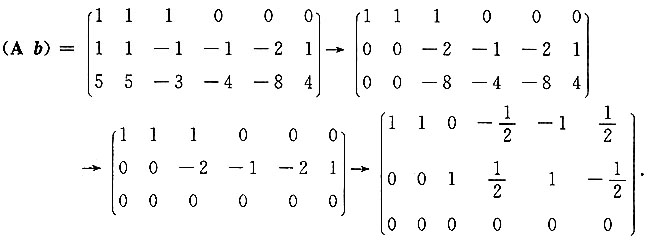
同解方程组为
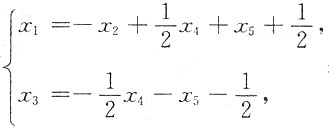
其中x
2，x
4，x
5为自由元．
令
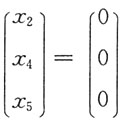
，得原方程组的一个特解
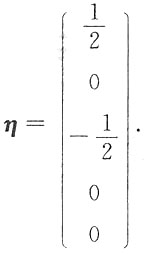
令
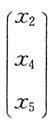
分别为
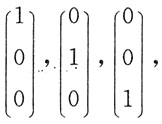
，得对应齐次方程组的一个基础解系为
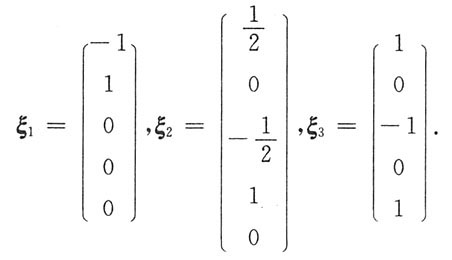
故方程组的通解为x=η+k
1ξ
1+k
2ξ
2+k
3ξ
3(k
1，k
2，k
3为任意常数)．
4. 求曲线y=x
2上一点P
0，使该点处的切线与曲线y=x
2、直线x=3及直线x=6所围图形面积最小，并求出最小面积．
设切点
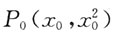
，由y'=2x，k=y'|
x=x0=2x
0，
得切线方程为
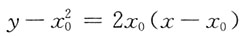
，即
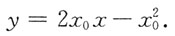
所围图形面积为
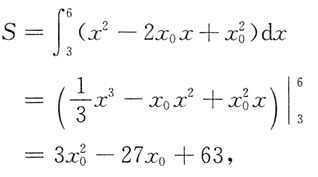
求导，得：S'=6x
0-27，令S'=0，得唯一驻点
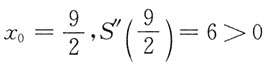
，故在
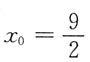
处取得极小值，又由于驻点唯一，则面积函数S在
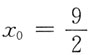
处取得最小值．
故P
0点坐标为
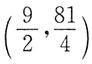
时所求面积最小，最小面积是
．
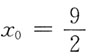
四、应用题(本题10分，将解答的主要过程、步骤和答案填写在相应位置上，写在其他位置上无效)1. 假设某企业在两个互相分割的市场上出售同一种产品，两个市场的销售量分别是
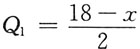
，Q
2=12-x，其中x为该产品在两个市场的价格(万元/吨)．该企业生产这种产品的总成本函数是C=2(Q
1+Q
2)+5．试确定x的值，使企业获得最大利润，并求出最大利润．
由已知条件得利润函数为
L=(Q
1+Q
2)x-C
=(Q
1+Q
2)x-2(Q
1+Q
2)-5
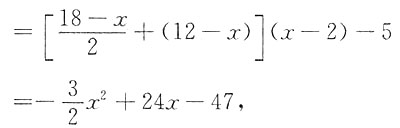
求导得：L'=-3x+24，
令L'=0，得驻点x=8．
根据实际情况，L存在最大值，且驻点唯一，则驻点即为最大值点．
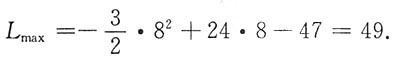
故当两个市场价格为8万元/吨时，企业获得最大利润，此时最大利润为49万元．
的定义域为______
即得x＞4．
______
，则|2A|=______
的凸区间是______
______
深色：已答题 浅色：未答题