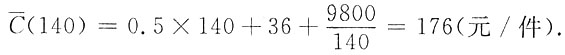一、单项选择题(在每小题给出的四个备选项中,选出一个正确的答案)1. 极限
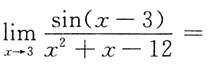
______
A.0
B.
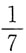
C.
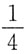
D.1
A B C D
B
[解析]
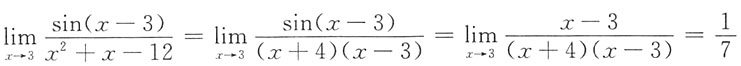
,故选B.
2. 设函数
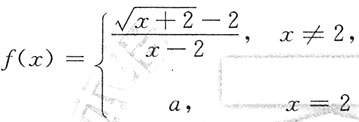
在x=2处连续,则a=______
A.4
B.
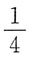
C.2
D.
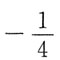
A B C D
B
[解析]
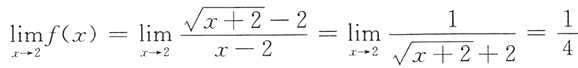
,又f(2)=a,根据连续的定义得
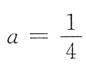
,故选B.
5. 设f'(cos
2x)=sin
2x,且f(0)=0,则f(x)=______
A.
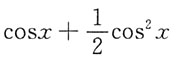
B.
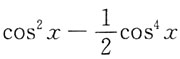
C.
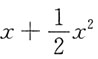
D.
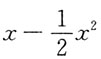
A B C D
D
[解析] f'(cos
2x)=sin
2x=1-cos
2x,f'(x)=1-x,
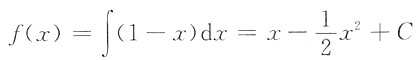
,又由f(0)=0得C=0,
所以
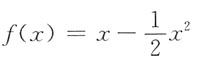
,故选D.
6. 过椭圆x
2+2y
2=27上横、纵坐标相等的点的切线斜率为______
A.-1
B.
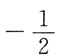
C.
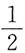
D.1
A B C D
B
[解析] 对椭圆x
2+2y
2=27两端使用隐函数求导法,得2x+4yy'=0,所以
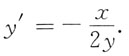
,因为x=y,得
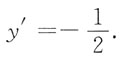
.
7. 下列级数中条件收敛的是______
A.
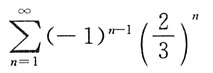
B.
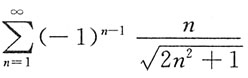
C.
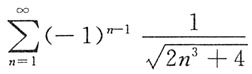
D.
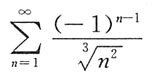
A B C D
D
[解析]
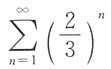
收敛,故A项绝对收敛;
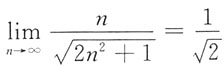
,故B项发散;
又

收敛,所以C项绝对收敛;
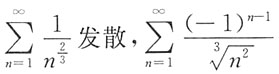
是交错级数,由莱布尼茨判别法知收敛,故D项条件收敛.
9. 微分方程sinxcosydy+cosxsinydx=0的通解为______
- A.sinxcosy=C
- B.cosxsiny=C
- C.sinxsiny=C
- D.cosxcosy=C
A B C D
C
[解析] 因为微分方程sinxcosydy+cosxsinydx=0,
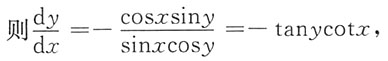
则-cotydy=cotxdx,所以-ln|siny|+C
1=ln|sinx|,
即ln|sinxsiny|=C
1,|sinxsiny|=e
C1,
故sinxsiny=C,(C为任意常数).
10. 设A,B均为n阶矩阵,|A|=2,|B|=-3,则|2A*B
-1|=______
A.
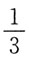
B.
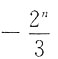
C.
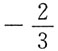
D.
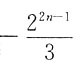
A B C D
D
[解析]
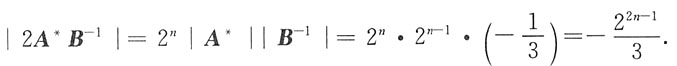
三、计算题(每小题10分,共40分.将解答的主要过程、步骤和答案填写在相应位置上,写在其他位置上无效)1. 平面图形由曲线
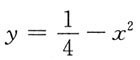
位于点

处的切线L以及y轴所围成,求该平面图形的面积.
2. 设u=x
2+sin2y+e
xy,求全微分du.
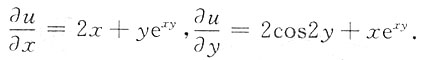
所以
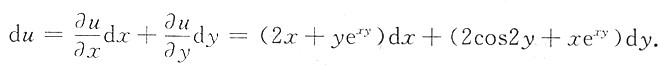
3. 求微分方程y'-2y-e
x=0的通解.
原方程可整理为y'-2y=ex,
这是一阶线性微分方程,其中P(x)=-2,Q(x)=ex.
所以原方程的通解为
y=e-∫P(x)dx(∫Q(x)e∫P(x)dxdx+C)
=e∫2dx(∫exe-∫2dxdx+C)
=e2x(∫e-xdx+C)=e2x(-e-x+C)
=-ex+Ce2x(其中C为任意常数).
4. 已知线性方程组
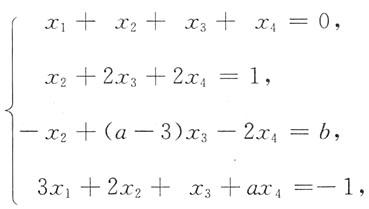
当a,b为何值时方程组有无穷多个解,并求出其通解.
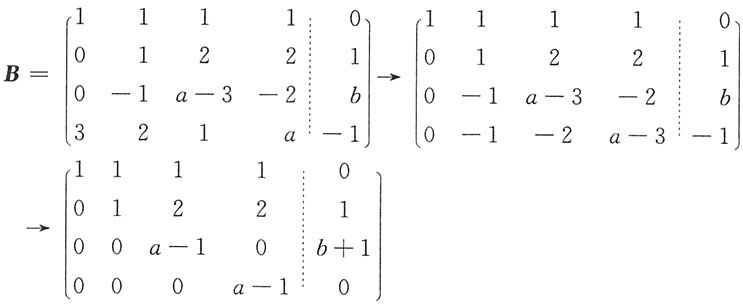
由于方程组有无穷多解,故
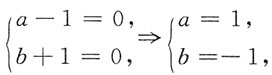
即a=1,b=-1时方程组有无穷多解,此时

同解方程组为
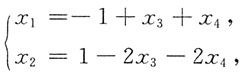
x
3,x
4为自由变量,
通解为(x
1,x
2,x
3,x
4)T=k
1(1,-2,1,0)
T+k
2(1,-2,0,1)
T+(-1,1,0,0)
T.
其中k
1,k
2为任意实数.
四、应用题(本题10分.将解答的主要过程、步骤和答案填写在相应位置上,写在其他位置上无效)1. 某厂每天生产Q件某种产品的成本函数为C(Q)=0.5Q
2+36Q+9800(元).为使平均成本最低,每天产量应为多少?此时,每件产品平均成本为多少?
因为
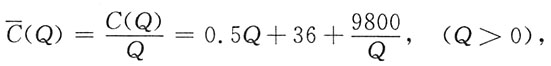
所以
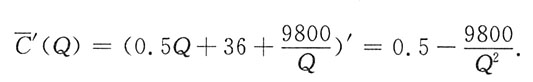
令

,得Q
1=140,Q
2=-140(舍去).
Q
1=140是函数
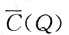
在其定义域内的唯一驻点,且该问题确实存在最小值.
所以Q
1=140是平均成本函数
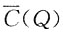
的最小值点,即为使平均成本最低,每天产量应为140件.
此时的平均成本为