银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
 ,参加跳远的占全体参加竞赛人数的
,参加跳远的占全体参加竞赛人数的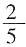 ,参加跳高的占全体参加竞赛人数的
,参加跳高的占全体参加竞赛人数的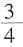 ,两项都参加的有12人。问全年级共有多少人?
,两项都参加的有12人。问全年级共有多少人?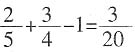 ,因此全体参加竞赛的人数有
,因此全体参加竞赛的人数有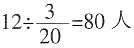 。这样,全年级应该有
。这样,全年级应该有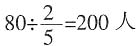 。
。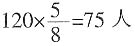 ,喜欢游泳的有
,喜欢游泳的有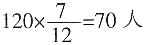 。由容斥原理公式,两种活动都不喜欢的有120-(75+70-43)=18人。
。由容斥原理公式,两种活动都不喜欢的有120-(75+70-43)=18人。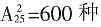 。
。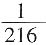
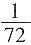


 ,所以所求概率为
,所以所求概率为 。
。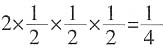 ,而出现两正面一反面或两反面一正面的概率为
,而出现两正面一反面或两反面一正面的概率为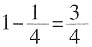 ,则甲应该要求乙每次至少给30元,才可考虑参加这个游戏。
,则甲应该要求乙每次至少给30元,才可考虑参加这个游戏。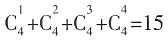 种币值。所以选择D。
种币值。所以选择D。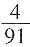
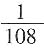

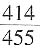
 种情况。由题意音乐、电影、游戏光盘各1张,有
种情况。由题意音乐、电影、游戏光盘各1张,有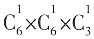 种情况,则所求概率为
种情况,则所求概率为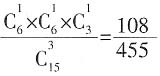 。
。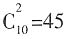 种选法,其中选出的2个人相邻的,有10种不同的选法,因此两个人不相邻。有45-10=35种选法。
种选法,其中选出的2个人相邻的,有10种不同的选法,因此两个人不相邻。有45-10=35种选法。 种不同方法;然后挑选乙角色,有
种不同方法;然后挑选乙角色,有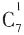 种角色;接着挑选丙角色、丁角色,依次有
种角色;接着挑选丙角色、丁角色,依次有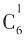 种不同方法、
种不同方法、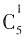 种不同方法。由乘法原理,不同的挑选方案共有
种不同方法。由乘法原理,不同的挑选方案共有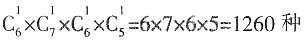 。
。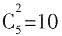 种,都是女职员共有
种,都是女职员共有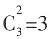 种,因此至少有一个男职员参加共有10-3=7种情况,可能性为
种,因此至少有一个男职员参加共有10-3=7种情况,可能性为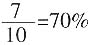 。
。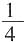
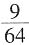
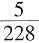
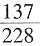
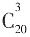 种情况,3件都是一级品的话,有
种情况,3件都是一级品的话,有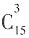 种情况,因此至少有一件为二级品的,有
种情况,因此至少有一件为二级品的,有 种情况,其概率是
种情况,其概率是 。
。 种情况。这里用到的是分步思想,所以应用乘法原理,共有3×24=72种排班方法。
种情况。这里用到的是分步思想,所以应用乘法原理,共有3×24=72种排班方法。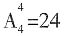 种情况,B和C本身又有2种情况,因此最终的编排方法有24×2=48种。
种情况,B和C本身又有2种情况,因此最终的编排方法有24×2=48种。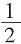
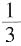
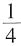

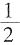 ,则乙最终取胜的可能性为
,则乙最终取胜的可能性为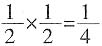 ,选C。
,选C。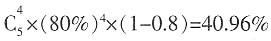 。
。| 学校 | 专业 | |||||||||||||
| 1. | 1. 2. | |||||||||||||
| 2. | 1. 2. | |||||||||||||
| 3. | 1. 2. | |||||||||||||
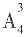 种选择,然后选择第一个学校的专业,有
种选择,然后选择第一个学校的专业,有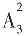 种选择,接着依次选择第二、第三个学校的专业,各有
种选择,接着依次选择第二、第三个学校的专业,各有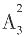 种选择,因此,一共有
种选择,因此,一共有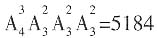 种不同的填法。
种不同的填法。 种方法,三个节目的全排列数为
种方法,三个节目的全排列数为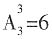 种。根据归一法可知.一共有120÷6=20种安排方法。
种。根据归一法可知.一共有120÷6=20种安排方法。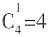 种方法,现在这4个节目形成5个空(包含两端),将剩余的一个节目插入这5个空中,有
种方法,现在这4个节目形成5个空(包含两端),将剩余的一个节目插入这5个空中,有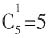 种方法,所以一共有4×5=20种方法。
种方法,所以一共有4×5=20种方法。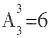 种;(2)有且只有两人被分到一个部门,此时不同的分配方案有
种;(2)有且只有两人被分到一个部门,此时不同的分配方案有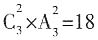 种。综上,共有18+6=24种不同的分配方案。
种。综上,共有18+6=24种不同的分配方案。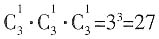 种,再减去三个人被分到同一科室的情况,为3种,故最终的分配方案为27-3=24种。
种,再减去三个人被分到同一科室的情况,为3种,故最终的分配方案为27-3=24种。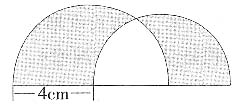
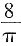
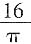
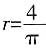 ,则每个圆形丝框的面积为
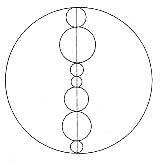
,则每个圆形丝框的面积为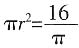 。
。

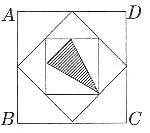

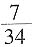
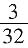
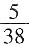
 ,最小正方形面积为第二大正方形面积的
,最小正方形面积为第二大正方形面积的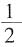 ,第二大正方形面积是最大正方形面积的
,第二大正方形面积是最大正方形面积的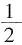 ,则阴影三角形的面积为
,则阴影三角形的面积为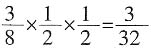 ,故选C。
,故选C。