一、选择题(1~15小题为学科专业知识测试题,16~25小题为综合知识测试题)4. 如图一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是______。
A.1
B.
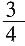
C.
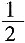
D.9
A B C D
C
[解析] 圆锥的侧面展开图是一个扇形,扇形的弧长等于底面圆周长。设圆锥底面半径为r,根据题意得
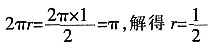
。
11. 已知F
1,F
2是椭圆
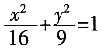
的两焦点,过点F
2的直线交椭圆于A,B两点。在△AF
1B中,若有两边之和是10,则第三边的长度为______。
A B C D
A
[解析] 根据椭圆定义,知△AF1B的周长为4a=16,故所求的第三边的长度为16-10=6。
13. 设等比数列{a
n}的前n项和为S
n,
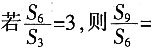
______。
A.2
B.
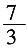
C.

D.3
A B C D
B
[解析] 设公比q,则
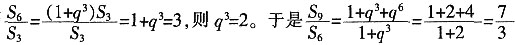
。
15. 已知抛物线C:y
2=8x焦点为F,准线与x轴交点为K,点A在C上且|AK|=
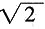
·|AF|,则△AFK的面积为______。
A B C D
B
[解析] 抛物线C:y
2=8x的焦点为F(2,0),准线为x=-2,K(-2,0),设A(x
0,y
0),过A点向准线作垂线AB,则B(-2,y
0),因|AK|=
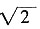
|AF|,又|AF|=|AB=x
0(-2)=x
0+2,由BK
2=Ak
2-AB
2得
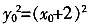
,即8x
0=(x
0+2)
2,解得A(2,±4),△AFK的面积为
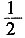
|KF|·|y
0|=
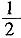
×4×4=8。
二、综合知识判断题3. 国家实行国家教育考试制度。国家教育考试由国务院教育行政部门确定种类,并由当地学校或者行政部门组织考试。
对 错
B
[解析] 国家实行国家教育考试制度。国家教育考试由国务院教育行政部门确定种类,并由国家批准的实施教育考试的机构承办。
三、填空题1. 将一颗骰子先后随机抛掷两次,设向上的点数分别为a,b,则关于x的方程ax+b=0有整数解的概率为______。
[解析] a、b共有36种不同的组合方法,若使x有整数解,a为1时,b共有6种取值方法,a为2时,b共有3种取值方法,a为3时,b共有2种取值方法,a为4、5、6时,b各有1种取值方法,共14种情况能使x有整数解,所以概率为
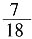
。
2. 与直线y=5相切,且与圆x
2+y
2-2x+2y-2=0外切的面积最小的圆的方程为______。
(x-1)2+(y-3)2=4
[解析] 已知圆的圆心为(1,-1),半径为2,所求圆若使半径最小一定有其圆心在x=1这条直线上,则所求圆的圆心横坐标为1,设所求半径为R,同时已知圆圆心到直线y=5的距离=2R+2=6,R=2,所求圆圆心到直线y=5的距离为R,可得圆心纵坐标为3。
3. 已知正数x、y满足方程
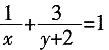
,则x+y的最小值是______。
[解析]
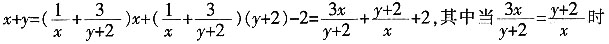
,该等式取得最小值为

。
4. 已知{a
n}是等差数列,若
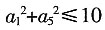
,则a
5+a
6+…+a
9的最大值是______。
25
[解析] 由已知得,(a
3-2d)
2+(a
3+2d)
2≤10,则
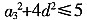
,又由柯西不等式
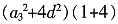
≥(a
3+4d)
2,即
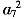
≤25,a
7最大取值为5,a
5+a
6+…+a
9=5a
7,所以答案为25。
5. 设椭圆的方程为

,(a>b>0),过右焦点F且不与x轴垂直的直线与椭圆交于P、Q两点,若在椭圆的右准线上存在点R,使△PQR为正三角形,则椭圆的离心率的取值范围是______。
(
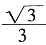
,1)
[解析] M为PQ的中点,QQ',MM',PP'分别垂直于右准线,
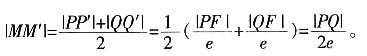
因为△PQR为正三角形,
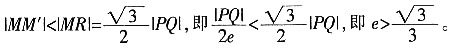
所以e的范围是(
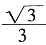
,1)。
6. 两个袋子中都装有红、黄、白三个小球,这些球除颜色外,形状、大小、质地等完全相同。搅匀后,在看不到球的条件下,随机分别从两个袋子中摸出一个球,摸出两球的颜色相同的概率是______。
[解析] 随机分别从两个袋子中摸出两球颜色相同的概率为
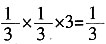
。
7. 已知反比例函数
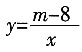
(m为常数)的图象经过点A(-1,6),则m的值为______。
2
[解析] 将点(-1,6)代入反比例函数
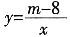
中,解得m=2。
8. 如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于______。
[解析] 根据同弧所对圆周角相等,得∠AED=∠ABD。所以在直角三角形ABC中tan∠ABC=
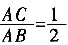
。即tan∠AED=
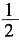
。
9. 曲线y=x
3+x+1在点(1,3)处的切线方程是______。
4x-y-1=0
[解析] 由题意得即曲线y'=3x2+1,曲线y=x3+x+1在点(1,3)处切线的斜率为4,所以切线方程为y-3=4(x-1),即4x-y-1=0。
10. 已知a,b为常数,若f(x)=x
2+4x+3,f(ax+b)=x
2+10x+24,则5a-b=______。
2
[解析] 由f(x)=x
2+4x+3,f(ax+b)=x
2+10x+24,得:(ax+b)
2+4(ax+b)+3=x
2+10x+24,即a
2x
2+2abx+b
2+4ax+4b+3=x
2+10x+24,比较系数得:
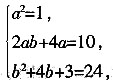
解得:a=-1,b=7,或a=1,b=3,则5a-b=2。
四、解答题(共45分)1.
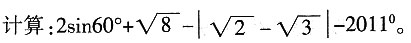
2. 当x=
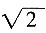
-1时,求代数式(x-1)
2-2(2-x)的值。
(x-1)
2-2(2-x)
=x
2-2x+1-4+2x
=x
2-3
当x=
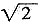
-1时,
原式

。
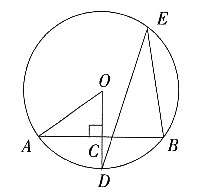
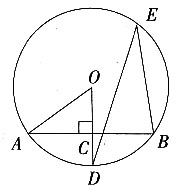
3. 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上。
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长。
(1)∵OD⊥AB,
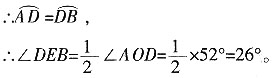
(2)∵OD⊥AB,
∴AC=BC,
∵△AOC为直角三角形,DC=3,OA=5,
由勾股定理,可得
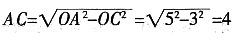
。
∴AB=2A C=8。
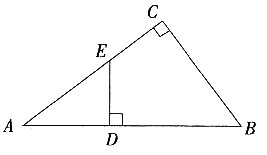
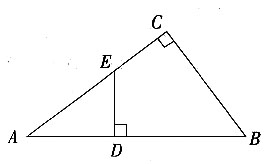
4. 如图,在△ABC中,∠C=90°,在AB边上取一点D,使BD=BC,过D作DE⊥AB交AC于E,AC=8,BC=6。求DE的长。
在△ABC中,∠C=90°,4C=8,BC=6,
∴AB=
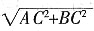
=10。
又∵BD=BC=6,
∴AD=AB-BD=4。
∵DE⊥AB,
∴∠ADE=∠C=90°。
∴△AED~△ABC。
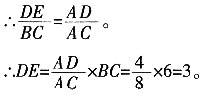
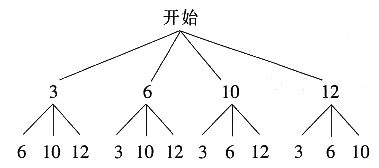
5. 请用树状图表示出两人抽牌可能出现的所有结果;
6. 求抽出的两张牌都是偶数的概率。
∵两张牌的数字都是偶数有6种结果,
∴P(偶数)
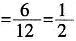
。
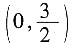 。
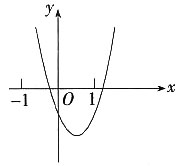
。7. 求二次函数的表达式,并在下面的网格中画出它的图象;
依题意可设此二次函数的表达式为产y=a(x+1)
2+2,又点(0,
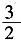
)在它的图象上,可得
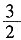
=a+2,解得a=
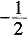
。
所求为y=
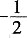
(x+1)
2+2。
令y=0,得x
1=1,x
2=-3。
画出其图象如下图。
8. 说明对于任意实数m,点M(m,-m
2)在不在这个二次函数的图象上。
若点M(m,-m
2)在此二次函数的图象上,
则-m
2=
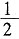
(m+1)
2+2
得m
2-2m+3=0。
方程的判别式:4-12=-8<0,该方程无解。
所以点M(m,-m
2)不在此二次函数的图象上。
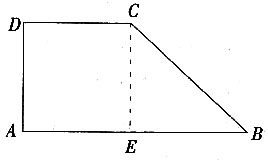
9. 如图,在梯形ABCD中,AB∥CD,∠A=90°,CD=4,AB=10,tan∠B=
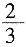
。求BC的长。
作CE⊥AB于E,
∵AB∥CD,∠A=90°
∴四边形AECD是矩形。
∴AE=DC=4。
∵AB=10,
∴BE=6。
在Rt△BEC中,
∵tan∠B=
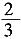
,BE=6。
∴CE=4。
由勾股定理,得

。
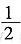 (∠B+∠C)=180°,故∠BOC=180°-
(∠B+∠C)=180°,故∠BOC=180°-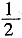 (∠B+∠C)=115°。
(∠B+∠C)=115°。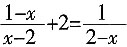 ,可知方程______。
,可知方程______。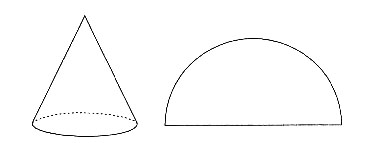
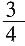
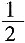
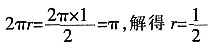 。
。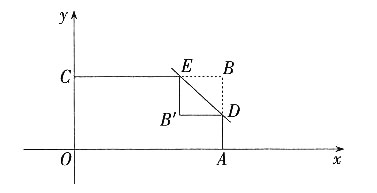
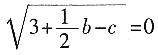 ,以a,b,c为边长组成的三角形面积等于______。
,以a,b,c为边长组成的三角形面积等于______。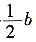 -c=0,所以b=4,c=5。易知a、b、c构成一个直角三角形,面积为
-c=0,所以b=4,c=5。易知a、b、c构成一个直角三角形,面积为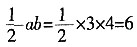 。
。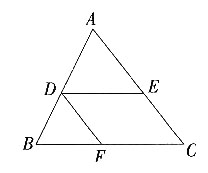
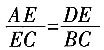

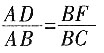

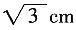 ,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥的侧面积为______。
,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥的侧面积为______。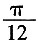
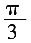
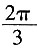
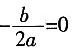
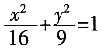 的两焦点,过点F2的直线交椭圆于A,B两点。在△AF1B中,若有两边之和是10,则第三边的长度为______。
的两焦点,过点F2的直线交椭圆于A,B两点。在△AF1B中,若有两边之和是10,则第三边的长度为______。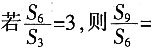 ______。
______。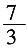

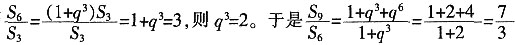 。
。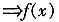 在(1-δ,1+δ)是凸的
在(1-δ,1+δ)是凸的 在此区间上,y=f(x)在点(1,f(1))即(1,1)处的切线y-1=f'(1)(x-1),即y=x在此曲线的上方(除切点外)。因此f(x)<x(x∈(1-δ,1+δ),x≠1)。
在此区间上,y=f(x)在点(1,f(1))即(1,1)处的切线y-1=f'(1)(x-1),即y=x在此曲线的上方(除切点外)。因此f(x)<x(x∈(1-δ,1+δ),x≠1)。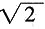 ·|AF|,则△AFK的面积为______。
·|AF|,则△AFK的面积为______。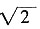 |AF|,又|AF|=|AB=x0(-2)=x0+2,由BK2=Ak2-AB2得
|AF|,又|AF|=|AB=x0(-2)=x0+2,由BK2=Ak2-AB2得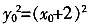 ,即8x0=(x0+2)2,解得A(2,±4),△AFK的面积为
,即8x0=(x0+2)2,解得A(2,±4),△AFK的面积为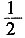 |KF|·|y0|=
|KF|·|y0|=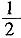 ×4×4=8。
×4×4=8。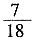
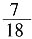 。
。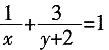 ,则x+y的最小值是______。
,则x+y的最小值是______。
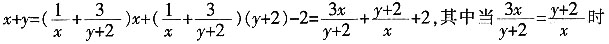 ,该等式取得最小值为
,该等式取得最小值为 。
。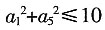 ,则a5+a6+…+a9的最大值是______。
,则a5+a6+…+a9的最大值是______。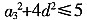 ,又由柯西不等式
,又由柯西不等式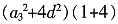 ≥(a3+4d)2,即
≥(a3+4d)2,即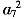 ≤25,a7最大取值为5,a5+a6+…+a9=5a7,所以答案为25。
≤25,a7最大取值为5,a5+a6+…+a9=5a7,所以答案为25。 ,(a>b>0),过右焦点F且不与x轴垂直的直线与椭圆交于P、Q两点,若在椭圆的右准线上存在点R,使△PQR为正三角形,则椭圆的离心率的取值范围是______。
,(a>b>0),过右焦点F且不与x轴垂直的直线与椭圆交于P、Q两点,若在椭圆的右准线上存在点R,使△PQR为正三角形,则椭圆的离心率的取值范围是______。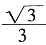 ,1)
,1)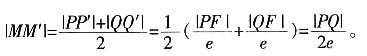
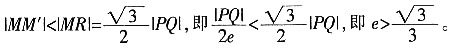
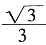 ,1)。
,1)。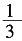
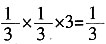 。
。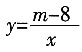 (m为常数)的图象经过点A(-1,6),则m的值为______。
(m为常数)的图象经过点A(-1,6),则m的值为______。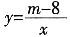 中,解得m=2。
中,解得m=2。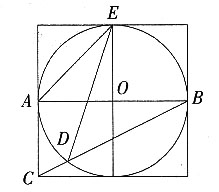
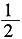
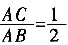 。即tan∠AED=
。即tan∠AED=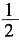 。
。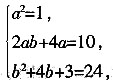 解得:a=-1,b=7,或a=1,b=3,则5a-b=2。
解得:a=-1,b=7,或a=1,b=3,则5a-b=2。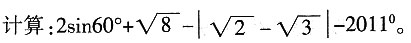

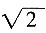 -1时,求代数式(x-1)2-2(2-x)的值。
-1时,求代数式(x-1)2-2(2-x)的值。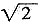 -1时,
-1时, 。
。
 。
。
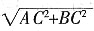 =10。
=10。

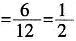 。
。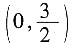 。
。
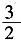 )在它的图象上,可得
)在它的图象上,可得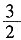 =a+2,解得a=
=a+2,解得a=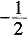 。
。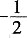 (x+1)2+2。
(x+1)2+2。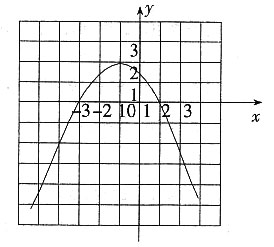
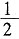 (m+1)2+2
(m+1)2+2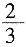 。求BC的长。
。求BC的长。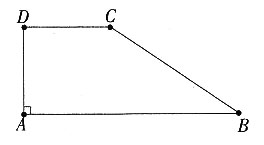
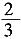 ,BE=6。
,BE=6。 。
。