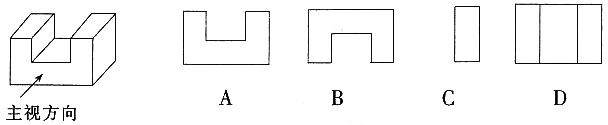
一、选择题(1~15小题为学科专业知识测试题,16~25小题为综合知识测试题)4. 在(x-1)(x+1)
8的展开式中的x
5系数是______。
A B C D
B
[解析] (x-1)(x+1)
8展开式中x
5的系数为
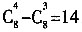
。
5. 已知圆O
1,O
2的半径分别是r
1=3,r
2=5若两圆相切,则圆心距O
1,O
2的值是______。
A B C D
C
[解析] 两圆半径分别为r1=3、r2=5,若两圆内切,则O1O2=5-3=2,若两圆外切,则O1O2=5+3=8,所以选C。
7. 若x
1,x
2是一元二次方程x
2+4x+3=0的两个根,则x
1x
2是______。
A B C D
B
[解析] 对于一元二次方程ax
2+bx+c=0(a≠0),若方程有两个实根x
1、x
2,则x
1+x
2=
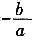
,x
1x
2=
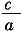
。由题意知x
1x
2=3。
10. 已知sinα-cosα=
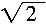
,α∈(0,π),则tanα=______。
A.-1
B.
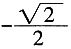
C.
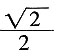
D.1
A B C D
A
[解析]
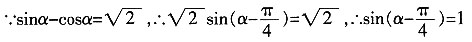
∵a∈(0,π),
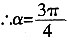
,∴tanα=-1,故选A。
11. 一质点受到平面上的三个力F
1,F
2,F
3(单位:牛顿)的作用而处于平衡状态,已知F
1,F
2成60°角,且F
1,F
2的大小分别为2和4,则F
3的大小为______。
A.6
B.2
C.
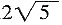
D.
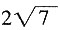
A B C D
D
[解析] 利用余弦定理
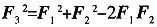
cos(180°-60°)=28,所以F
3的大小为
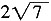
。
14. 投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n-mi)为实数的概率为______。
A.
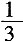
B.
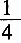
C.
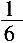
D.
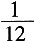
A B C D
C
[解析] 因为(m+ni)(n-mi)=2mn+(n
2-m
2)i为实数,所以n
2=m
2,故m=n,则可以取1、2…6,共6种可能,所以
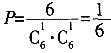
。
15. 在△ABC中,AB=2,AC=3,
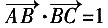
,则BC=______。
A.
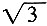
B.

C.
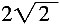
D.
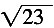
A B C D
A
[解析] 由题目可知
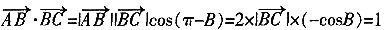
。
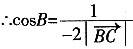
。又由触定理知
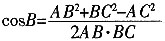
,解得BC=
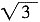
。
二、综合知识判断题1. 1948年8月1日,新疆保卫和平民主同盟在乌鲁木齐成立。
对 错
B
[解析] 1948年8月1日,新疆保卫和平民主同盟在伊宁成立。
2. 马克思主义民族理论的核心是世界和平和民族团结。
对 错
B
[解析] 马克思主义民族理论的核心是民族平等和民族团结。
4. 明知校舍或者教育教学设施有危险,而不采取措施,造成人员伤亡或者重大财产损失的,对直接负责的主管人员和其他直接责任人员,给予行政处分。
对 错
B
[解析] 明知校舍或者教育教学设施有危险,而不采取措施,造成人员伤亡或者重大财产损失的,对直接负责的主管人员和其他直接责任人员,依法追究刑事责任。
5. 位于塔里木的交河故城和高昌故城,距今已有2000多年历史,是吐鲁番千年沧桑历史的见证。
对 错
B
[解析] 位于吐鲁番的交河故城和高昌故城,距今已有2000多年历史,是吐鲁番千年沧桑历史的见证。
三、填空题1. 两块一样重的合金,一块合金中铜与锌的比是3:7,另一块合金中铜与锌的比是2:3。现将两块合金合成一块,新合金中铜与锌的比是______。
2.
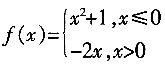
,若f(x)______。
3. 已知sin(α-π)=
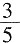
,则cos2α=______。
[解析] 由题意sin(π-α)=sinα=
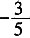
,cos2α=1-2sin
2α=

。
4. 关于x的不等式
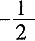
x
2+2x>mx的解集为{x|0<x<2},则m=______。
1
[解析] 将方程转化为x(x-4+2m)<0,由此方程解集为{x|0<x<2},知4-2m=2,故m=1。
5. 已知等比数列{a
n}中,a
3=12,a
5=48,那么a
7=______。
192
[解析]
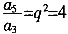
,a
3,a
5,a
7是以4为公比的等比数列,故a
7=192。
6. 函数

的定义域为______。
[解析] 由题意得log
0.5(4x
2-3x)≥0,则由对数函数性质得0<4x
2-3x≤1,即
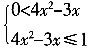
。求得函数的定义域为:
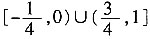
。
7. 在由数字0,1,2,3,4,5所组成的没有重复数字的四位数中,不能被5整除的数共有______个。
192
[解析] 没有重复数字的四位数共有5×5×4×3=300个。末位数是0的数有5×4×3=60个,末位数是5的数有4×4×3=48个,所以不能被5整除的数有300-60-48=192个。
8. 若3
a=0.618,a∈[k,k+1),k∈Z,则k=______。
-1
[解析] 3a=0.618,a∈[-1,0),又由a∈[k,k+1)且k∈Z,故得k=-1。
9. 在1~2003这些自然数中,能被2整除或能被5整除的数共有______个。
1201
[解析] 1~2003中能被2整除的有1001个;1~2003中能被5整除的有400个,既能被2又能被5整除的数有200个。故在1~2003这些自然数中,能被2整除或能被5整除的数共有1001+400-200=1201个。
10. 在同一平面上,2个点可以连成一条线段,10个点可以连成______条线段。
四、解答题(共45分)1. 二次函数的图象经过点(1,2)和(0,-1)且对称轴为x=2,求二次函数解析式。
设所求二次函数的解析式为:y=a(x-2)
2+k
由已知条件可得:
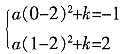
解得:
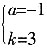
∴所求二次函数的解析式为:y=-(x-2)
2+3,
即y=-x
2+4x-1。
2. 已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=4cm。
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若2sinA-1=0,求⊙O的直径。
(1)∵AB为⊙O的直径
∴AC⊥BC
∵OD∥BC
∴AC⊥OD
(2)∵OD∥BC,O为AB的中点
∴OD为△ABC的中位线
∵BC=4cm
∴DD=2cm
(3)∵2sinA-1=0
∴∠A=30°
在△ABC中,∠ACB=90°,∠A=30°,BC=4cm,
∴AB=8cm。
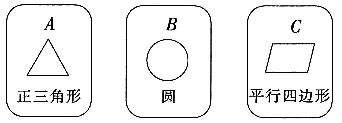
3. 用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A,B,C表示);

| 结果
|
AA
|
AB
|
AC
|
BA
|
BB
|
BC
|
CA
|
CB
|
CC
|
| 两轴对称图形
|
是
|
是
|
不是
|
是
|
是
|
不是
|
不是
|
不是
|
不是
|
4. 求摸出两张牌面图形都是轴对称图形的纸牌的概率;
摸出的两张牌面都是轴对称图形的纸牌的概率是
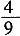
。
5. 小华和小明玩游戏,规定:若摸出两张牌面图形都是轴对称图形的纸牌,则小华赢;否则,小明赢。请你说明此规定是否公平。
此规定不公平。因为小华赢的概率是
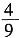
,小明赢的概率是
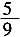
。
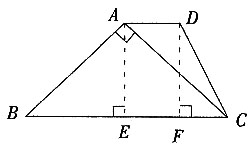
6. 如图,在梯形ABCD中,AD∥BC,AB⊥AC,AB=45°,AD=
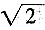
,BC=
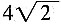
,求DC的长。
分别过点A,D作AE⊥BC于点E,DF⊥BC于点F。
∴AE∥DF
又∵AD∥BC,
∴四边形AEFD是矩形。
∴EF=AD=
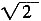
。
∵AB⊥AC,∠B=45°,BC=
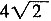
,
∴AB=AC ∴
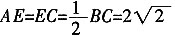
。
∴DF=AE=
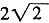
。
CF=EC-EF=
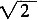
,
在Rt△DFC中,∠DFC=90°,DF=
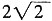
,CF=
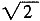
,
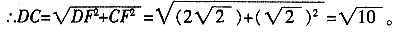
7. 如图,四边形OABC是面积为4的正方形,函数
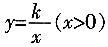
的图象经过点B。
(1)求k的值;
(2)将正方形OABC分别沿直线AB,BC翻折,得到正方形MABC'和NA'BC。设线段MC',NA'分别与函数
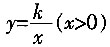
的图象交于点F,E。求线段EF所在直线的解析式。
(1)∵B(2,2),∴k=4。
(2)由题意可知,M(4,0),N(0,4)
可求得F(4,1),E(1,4)。
设直线EF的解析式为y=kx+b,
可求得k=-1,b=5。
所以,线段EF所在直线的解析式为
y=-x+5。
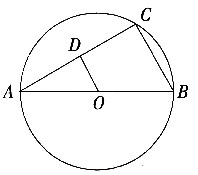
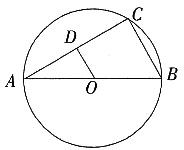
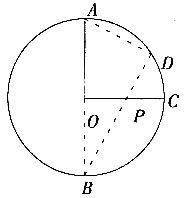
8. 如图,OA、OC是⊙O的半径,OA=1,且OC⊥OA,点D在

,在OC求一点P,使PA+PD最小,并求这个最小值。
延长AO交⊙O于B,连结BD交OC于点P,则点P为所求。连结AD。
∵AB为⊙O的直径,
∴∠ADB=90°
∵OC⊥OA,
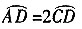
,
∴∠ABD=30°
∵OA=1
∴AB=2
∴BD=
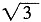
即PA+PD最小值为
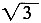
。
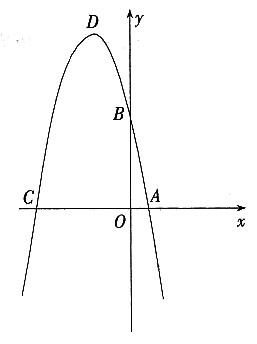
9. 如图,抛物线y=-x
2+bx+c与x轴的一个交点是A,与y轴的交点是B,且OA、OB(|OA<|OB|)的长是方程x
2-6x+5=0的两个实数根。
(1)求A、B两点的坐标;
(2)求出此抛物线的解析式及顶点D的坐标;
(3)求出此抛物线与x轴的另一个交点C的坐标;
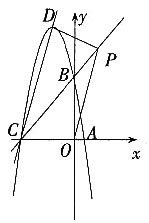
(4)在直线BC上是否存在一点P,使四边形PDCO为梯形?若存在,求出P点坐标,若不存在,说明理由。
(1)∵x
2-6x+5=0的两个实数根为x
1=1,x
2=5,
OA、OB(OA<OB)的长是方程x
2-6x+5=0的两个实数根,
∴OA=1,OB=5
∴A(1,0),B(0,5)。
(2)∵抛物线y=-x
2+bx+c与x轴的一个交点是A,与y轴的交点是B。
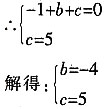
∴所求二次函数的解析式为:y=-x
24x+5。
顶点坐标为:D(-2,9)。
(3)此抛物线与x轴的另一个交点C的坐标为(-5,0)。
(4)直线CD的解析式为:y=3x+15,
直线BC的解析式为:y=x+5。
①若以CD为底,则OP∥CD,
直线OP的解析式为:y=3x。
于是有
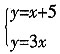
解得:
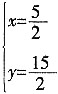
∴点P的坐标为
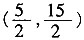
。
②若以OC为底,则DP∥CO。
直线DP的解析式为:y=9。
于是有

解得:
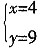
∴点P的坐标为(4,9)。
∴在直线BC上存在点P,使四边形PDCO为梯形且P点坐标为
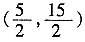
或(4,9)。
 。
。
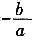 ,x1x2=
,x1x2=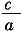 。由题意知x1x2=3。
。由题意知x1x2=3。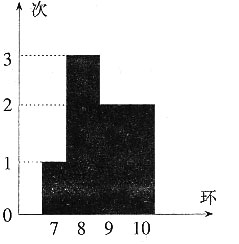
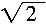 ,α∈(0,π),则tanα=______。
,α∈(0,π),则tanα=______。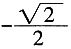
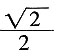
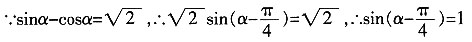
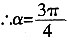 ,∴tanα=-1,故选A。
,∴tanα=-1,故选A。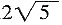
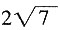
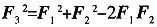 cos(180°-60°)=28,所以F3的大小为
cos(180°-60°)=28,所以F3的大小为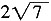 。
。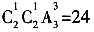 ;若小张、小赵都入选,则有选法
;若小张、小赵都入选,则有选法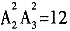 ,共有选法36种,选A。
,共有选法36种,选A。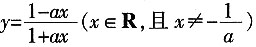 的反函数是______。
的反函数是______。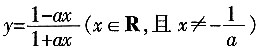
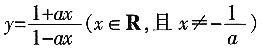
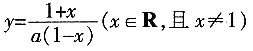
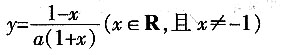
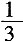
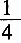
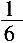
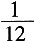
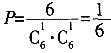 。
。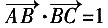 ,则BC=______。
,则BC=______。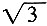

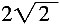
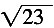
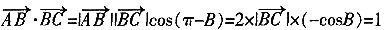 。
。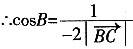 。又由触定理知
。又由触定理知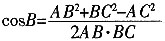 ,解得BC=
,解得BC=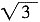 。
。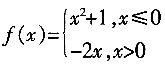 ,若f(x)______。
,若f(x)______。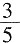 ,则cos2α=______。
,则cos2α=______。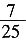
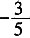 ,cos2α=1-2sin2α=
,cos2α=1-2sin2α= 。
。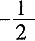 x2+2x>mx的解集为{x|0<x<2},则m=______。
x2+2x>mx的解集为{x|0<x<2},则m=______。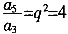 ,a3,a5,a7是以4为公比的等比数列,故a7=192。
,a3,a5,a7是以4为公比的等比数列,故a7=192。 的定义域为______。
的定义域为______。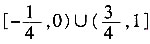
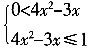 。求得函数的定义域为:
。求得函数的定义域为: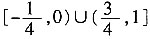 。
。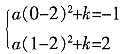
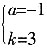

 。
。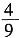 ,小明赢的概率是
,小明赢的概率是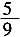 。
。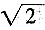 ,BC=
,BC=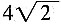 ,求DC的长。
,求DC的长。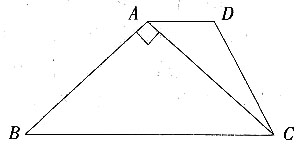
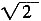 。
。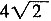 ,
,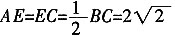 。
。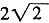 。
。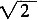 ,
,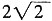 ,CF=
,CF=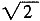 ,
,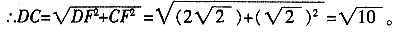
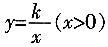 的图象经过点B。
的图象经过点B。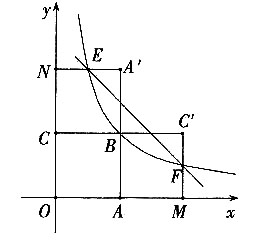
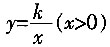 的图象交于点F,E。求线段EF所在直线的解析式。
的图象交于点F,E。求线段EF所在直线的解析式。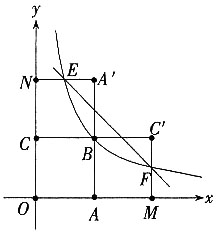
 ,在OC求一点P,使PA+PD最小,并求这个最小值。
,在OC求一点P,使PA+PD最小,并求这个最小值。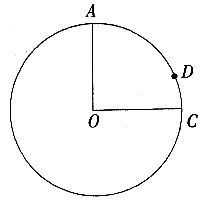
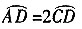 ,
,
 。
。
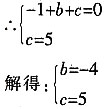
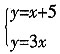 解得:
解得: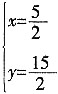
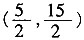 。
。 解得:
解得: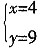
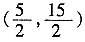 或(4,9)。
或(4,9)。