一、逻辑推理题下列每题给出的A、B、C、D、E五个选项中。只有一项是符合试题要求的。 二、数学单项选择题2. 已知f'(x)=
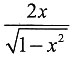
,则
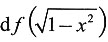
=______.
A.-2xdx
B.
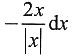
C.
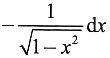
D.
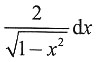
A B C D
B
[解析]

3.
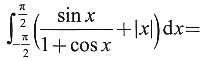
______.
A.0
B.
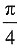
C.
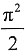
D.
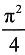
A B C D
D
[解析] 此题考查定积分的计算,需要用奇偶函数在对称区间上的性质化简.
5. 使不等式
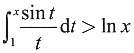
成立的x的范围是______.
A.(0,1)
B.
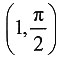
C.
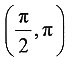
D.(π,+∞)
A B C D
A
[解析] 设f(x)=
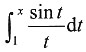
-ln x,则
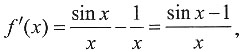
由于在(0,+∞)内f'(x)≤0,所以函数f(x)在(0,+∞)内单调不增.
又因为f(1)=0,所以当x∈(0,1)时,f(x)≥0;当x∈(1,+∞)时,f(x)≤0,即只有在(0,1)内才有f(x)≥0,而且是f(x)>0(因为x∈(0,1)时,f'(x)<0,因此f(x)是单调递减的),故只有
在(0,1)内不等式
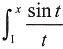
dt>ln x成立.
6. 已知函数f(x,y)=
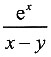
,则______.
A.
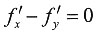
B.
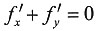
C.
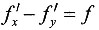
D.
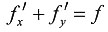
A B C D
D
[解析] 因为
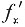
(x,y)=
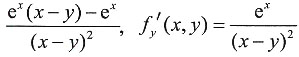
.所以
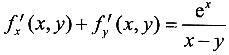
=f(x,y).故选D.
7. 设随机变量X的概率分布为P{X=k}=
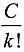
(k=0,1,2,…),则E(X
2)=______.
A B C D
D
[解析] 由分布律性质,有
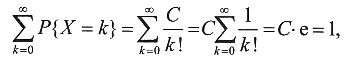
因此C=e
-1,于是P{X=k}=
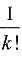
e
-1(k=0,1,2,…),由此可知,随机变量X服从参数λ=1的泊松分布,进而有EX=DX=λ=1,所以
E(X
2)=DX+(EX)
2=1+1=2.
9. 设
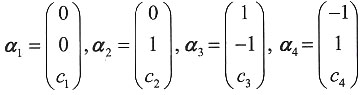
,其中,c
1,c
2,c
3,c
4为任意常数,则下列向量组线
- A.α1,α2,α3
- B.α1,α2,α4
- C.α1,α3,α4
- D.α2,α3,α4
A B C D
C
[解析] 由于|α
1,α
3,α
4|=
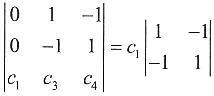
=0,可知向量组α
1,α
3,α
4线性相关,故选C.
10. 设A为m×n矩阵,R(A)=n-2,α
1,α
2,α
3,是非齐次线性方程组Ax=b的3个线性无关的解向量,k
1,k
2是任意常数,则此方程组的通解是______.
- A.k1(α1-α2)+k2(α2+α3)+α1
- B.k1(α1-α3)+k2(α1+α2)+α1
- C.k1(α1-α3)+k2(α1+α3)+α2
- D.k1(α1-α2)+k2(α2)-α3))+α2)
A B C D
D
[解析] 因为非齐次线性方程组Ax=b满足R(A)=n-2,所以导出组Ax=O的基础解系中含有2个线性无关的解向量.又α1,α2,α3是Ax=b的3个线性无关的解向量,所以α1-α2,α2-α3均是Ax=O的解,并且容易验证α1-α2,α2-α3线性无关,它们是Ax=O的一个基础解系,因此,Ax=b的通解为k1(α1-α2)+k2(α2-α3)+α2.
三、数学计算题1.
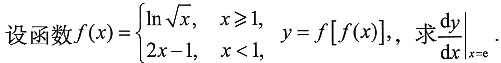
2. 设y=e
3u,u=f(t),t=lnx,其中f(u)可微,求dy。
解:dy=e
3ud(3u)=3e
3udu=3e
3uf'(t)dt=3e
3uf'(t)
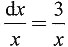
f'(ln x)e
3f(ln x)dx.
3. 设f(x)=φ(a+bx)-φ(a-bx),其中,φ(x)在(-∞,+∞)内有定义,且在x=a处可导,求f'(0).
解:若b=0时,则f(x)≡0,故f'(0)=0.若b≠0时,由导数的定义,可得
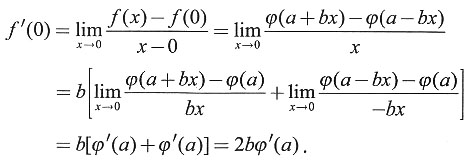
4. 设点(1,3)是曲线y=x
3+ax
2+bx+c的拐点,且x=2是此曲线的极值点,求a,b,c.
解:点(1,3)在曲线y=x
3+ax
2+bx+c上,所以有1+a+b+c=3.又因为x=2是曲线的极值点,由取得极值的必要条件,有
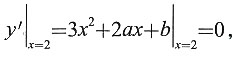
即12+4a+b=0.点(1,3)是曲线的拐点,所以有
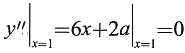
,即6+2a=0.解方程组
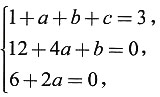
得到a=-3,b=0,c=5.
5.
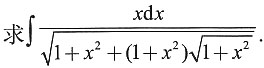
解:此题略加变形可得
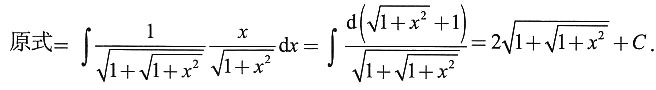
[解析] 对于多层根号的积分,往往先略加变形,以便寻找简便的途径,不宜盲目采用去根号的方法.
6.
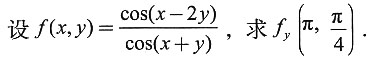
解:法一 先求偏导函数f
y(x,y),再求
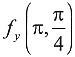
.由于
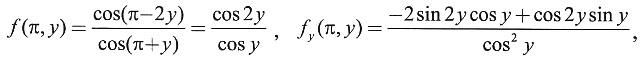
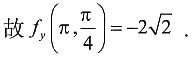
法二 利用偏导数f
y(x
0,y
0)即为一元函数f(x
0,y)在y
0处的导数,f
x(x
0,y
0)为f(x,y
0)在x
0处的导数.由于
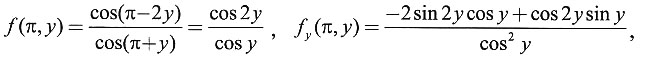

7. 求X的分布函数F(x);
解:F(x)=P{X≤x}=
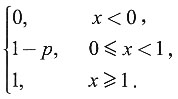
[解析] 离散型随机变量的分布函数求法,离散型随机变量函数的概率分布求法.
8. 令Y=F(X),求Y的概率分布.
解:由于Y=F(x)=
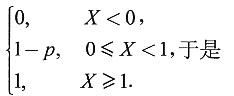
P{Y=0}=P{x<0}=0,
P{Y=1-p}=P{0≤X<1}=P{X=0}=1-p,
P{Y=1}=P{X≥1}=P{X=1}=p.
所以Y的概率分布为
9. 设随机变量X~N(0,1),随机变量
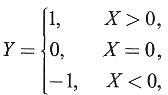
,的数学期望.
解:EY=-1·P{Y=-1}+0·P{Y=0}+1·P{Y=1}
=1·P{X<0}+1·P{X>0}=1×
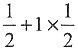
=1.
10. 设矩阵
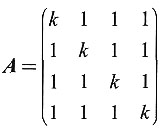
,且R(A)=3,求k的值.
解:由于A为4阶方阵,又R(A)=3知|A|=0,即|A|=(k+3)(k-1)3=0,解得k=-3或k=1.由于当k=1时,R(A)=1,故k=-3.
[解析] 因为R(A)<4,所以|A|=0.利用|A|=0解出参数k,再验证k取何值时R(A)=3.
11. 设
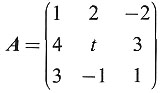
,B为三阶非零矩阵,且AB=O,求t.
解:因B为三阶非零矩阵,又AB=O,故B的列向量为方程组Ax=O的解且为非零解,故|A|=0,解得t=-3.
四、写作题共40分。其中论证有效性分析20分,论说文20分。1. 论证有效性分析:分析下面的论证在概念、论证方法、论据及结论等方面的有效性,600字左右。(论证有效性分析的一般要点是:概念特别是核心概念的界定和使用是否准确并且前后一致,有无各种明显的逻辑错误,论证的论据是否成立并且支持结论,结论成立的条件是否充分,等等。)
大众传播中的文章是否有必要像学术研究中的论文一样强调逻辑的绝对严密?不仅不必要,而且不应该。
投入大众传播的文章,其根本目的是传达正确的思想,而达到这个目的的前提是有足够多的受众。为了有足够多的受众,一定要用群众喜闻乐见的表达手法。几十年前,红军用“打土豪、分田地”“红军主张讨老婆不要钱”这样的口号,动员了广大农民,形成社会潮流冲击原有的社会结构,这种成功的经验是今天的人们应该借鉴的。
若一味追求严谨,做出些曲高和寡的文章,无异于将我们的阵地拱手让出。如果让煽动者、蛊惑者们钻了空子,利用逻辑性的表达方式传播邪恶的思想,后果将不堪设想。写文章的人的第一职责应该是正确而有效地引导舆论,而不是让自己的文章虽然无懈可击但不为大众接受。
我们可以设想这样一种情况,一篇充满比喻、排比的激情澎湃的评论,即使被学问家们在逻辑上批得体无完肤,只要它引起了社会的关注,激起了群众的热情,给群众以启迪,引发了群众的行动,那么这就是一篇成功的评论。学问家们固然可以有些“众人皆醉我独醒”的学者气,但评论家们一定不能,因为一篇脱离了大众的评论没有任何意义。
从另一个方面来说,投入大众传播的文章往往不像学术论文那样有较长的篇幅,而在很多的篇幅内要想进行充分的论证是很难做到的。因此,任何一篇文章或多或少都会有逻辑上的缺陷。有人担心这样的文章里会用煽动群众的方式传播错误观点和虚假信息。但是那些所谓逻辑严谨的文章,里面同样不缺少错误观点和虚假信息。
题干材料存在的主要逻辑漏洞有:
(1)材料认为讲求逻辑就是脱离大众,这预设了受众都是没有逻辑性的,这样的预设未必成立。
(2)为了有足够多的受众,很可能需要一篇文章的作者从形式和内容两个方面着手,材料只考虑到了一个方面。“群众喜闻乐见的表达手法”是就形式而言,“逻辑性”是就内容而言,二者并非矛盾对立的关系。讲究逻辑的严密并不意味着一定没有喜闻乐见的形式。
(3)几十年前红军的口号并不是文章,用这样的例子来论证写文章的方法是无效的。况且,由于社会、政治、经济环境的变化,几十年前的经验放到现在的社会,可能并不适用。
(4)“正确而有效地引导舆论”和“文章无懈可击但不为大众接受”并不是两种仅有的可能,讲求逻辑而有足够的受众也是可能的,“追求严谨”并不必然导致“曲高和寡”。
(5)如果一篇文章缺少逻辑性,如何判断其传播的是“正确的思想”?
(6)如果一篇文章不讲求逻辑严密性,即使“喜闻乐见”了,也只会出现谬误。如果谬误能够激起群众热情而付之行动,那也未必是成功的,也许会如材料所言,“让煽动者、蛊惑者们钻了空子,利用大众喜闻乐见的表达方式传播邪恶的思想,后果不堪设想”。
(7)群众热情和群众行动未必是判断一篇评论是否成功的标准,就算是,这也未必是唯一标准;也许还需要“正确的思想”以及合理的论证。
(8)即使评论文章不需要强调逻辑严密性,也推不出来投入大众传播中的所有文章都不需要逻辑的严密性。
(9)材料试图用否定讲逻辑的可能性的方法来否定讲逻辑的必要性。一篇文章具有严密的逻辑性或许是困难的,但并不能说明这是不必要的。
(10)即便逻辑严谨的文章也可能有这样那样的问题,但这不能说明逻辑不严谨的文章传递虚假信息和错误观点就是合理的,材料转移了论题。
(指出其他逻辑错误,只要言之成理,也可得分。)
2. 论说文:根据以下材料,自拟题目写一篇论说文,600字左右。
2016年6月,上海市停止实行70岁以上老人持“敬老卡”免费乘坐公交车及地铁,改为发放老年综合津贴。记者实地观察发现,公交车站及地铁上的老年乘客明显减少。据巴士公交二、三公司48、49路车队反映,当天老年乘客比以往下降了8成以上。
论说文思考角度提示
每个人的需求和消费习惯是极其个性化的,硬塞到手里的有可能是你不需要的。免费乘车即是如此,受限于活动范围、出行习惯、消费偏好、身体状况等因素,并非所有老年人都有乘坐公交车的“刚需”。
变“乘车免费”为“综合津贴”,就是把消费选择权交给老人,他们可以把这些钱用来乘车、购物、健身、听戏……可见,取消乘车免费,不是拿掉了福利,而是转移了福利,让福利以另一种形式实现。通过福利变现钱,老年人的福利需求就可以进行个性化配置。
免费往往会刺激无效需求,导致对公共资源的过度使用。公共交通出行,尤其在北京、上海、广州这样的大城市,高峰时段的拥挤是每个乘车人都躲不过的一段不愉快体验,更造成了让座纠纷对社会公德的反复击打。
公交免费的取消,有可能压缩一部分可有可无的需求,将“为省几毛鸡蛋钱绕城一圈”的现象挤压出去。从这个角度而言,免费政策,不一定对应着最大福利,却肯定对应着膨胀了的公共成本。这种情况下,还是要依靠消费、需求、供给的真实市场信号来调节资源,这样才会更贴切地对接个人生活。
转移福利符合福利分配的经济原则和市场原则,也会一改“免费的就是好的”的认知,指导人们走出某种福利错觉,让老年人的权益保障更真实。
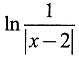 ,则x=2是f(x)的______.
,则x=2是f(x)的______.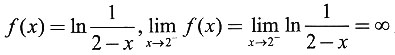 ,则x=2是f(x)的第二类间断点.
,则x=2是f(x)的第二类间断点.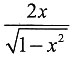 ,则
,则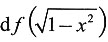 =______.
=______.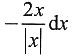
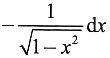
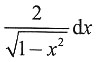

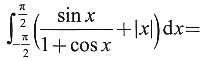 ______.
______.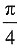
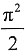
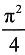
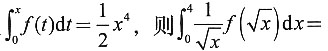 ______.
______.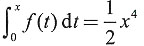 知,f(x)=2x3,于是
知,f(x)=2x3,于是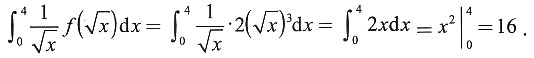
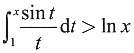 成立的x的范围是______.
成立的x的范围是______.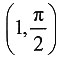
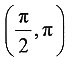
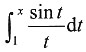 -ln x,则
-ln x,则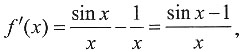
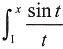 dt>ln x成立.
dt>ln x成立.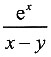 ,则______.
,则______.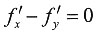
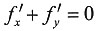
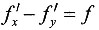
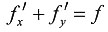
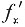 (x,y)=
(x,y)=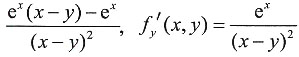 .所以
.所以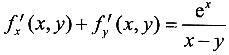 =f(x,y).故选D.
=f(x,y).故选D.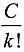 (k=0,1,2,…),则E(X2)=______.
(k=0,1,2,…),则E(X2)=______.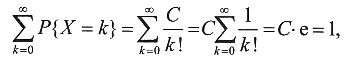
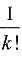 e-1(k=0,1,2,…),由此可知,随机变量X服从参数λ=1的泊松分布,进而有EX=DX=λ=1,所以
e-1(k=0,1,2,…),由此可知,随机变量X服从参数λ=1的泊松分布,进而有EX=DX=λ=1,所以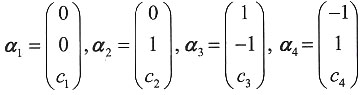 ,其中,c1,c2,c3,c4为任意常数,则下列向量组线
,其中,c1,c2,c3,c4为任意常数,则下列向量组线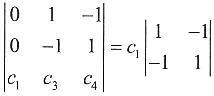 =0,可知向量组α1,α3,α4线性相关,故选C.
=0,可知向量组α1,α3,α4线性相关,故选C.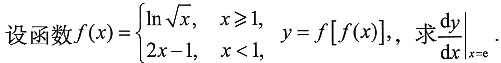

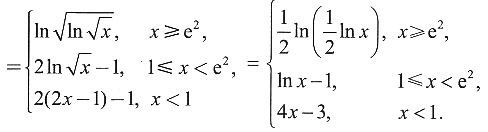
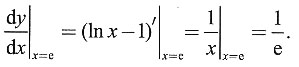
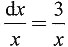 f'(ln x)e3f(ln x)dx.
f'(ln x)e3f(ln x)dx.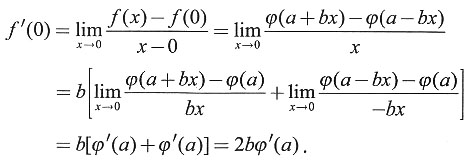
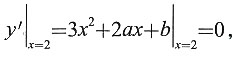 即12+4a+b=0.点(1,3)是曲线的拐点,所以有
即12+4a+b=0.点(1,3)是曲线的拐点,所以有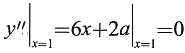 ,即6+2a=0.解方程组
,即6+2a=0.解方程组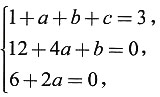 得到a=-3,b=0,c=5.
得到a=-3,b=0,c=5.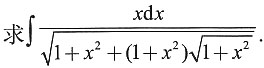
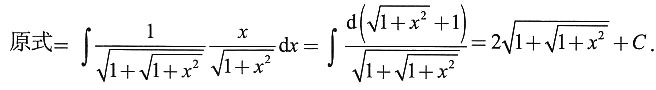
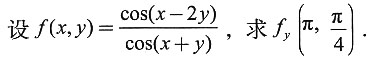
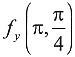 .由于
.由于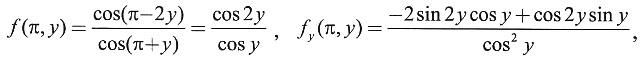
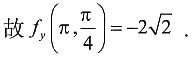
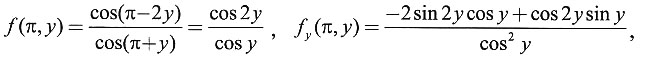

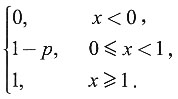
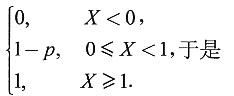
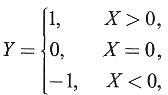 ,的数学期望.
,的数学期望. =1.
=1.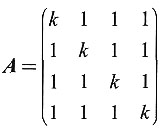 ,且R(A)=3,求k的值.
,且R(A)=3,求k的值.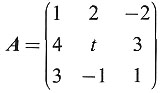 ,B为三阶非零矩阵,且AB=O,求t.
,B为三阶非零矩阵,且AB=O,求t.