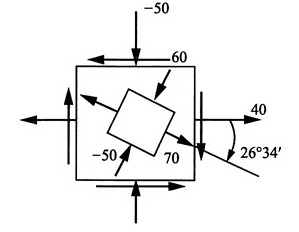
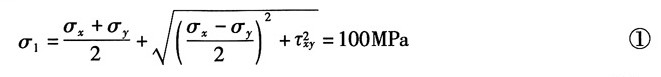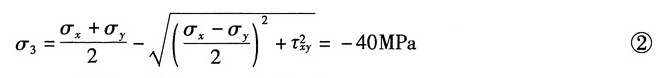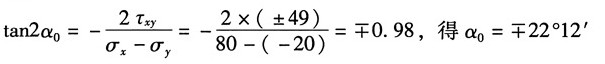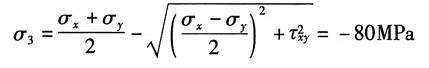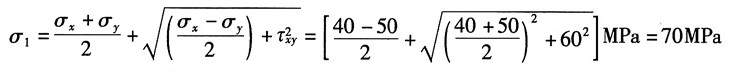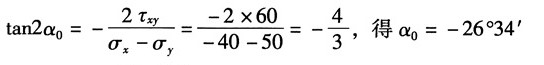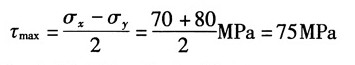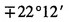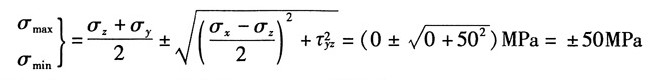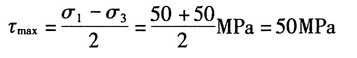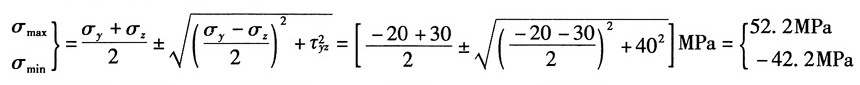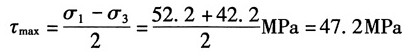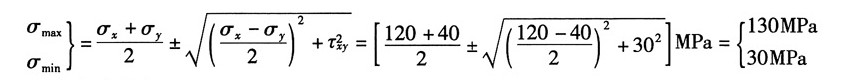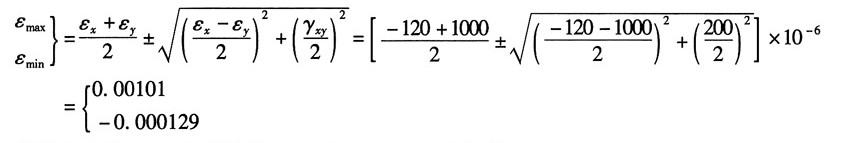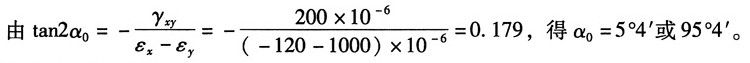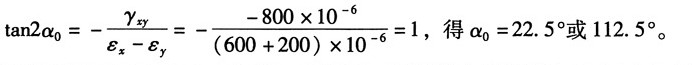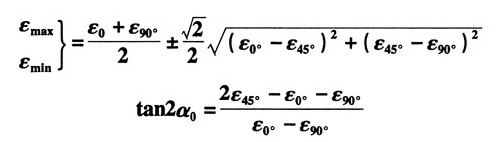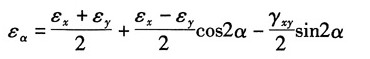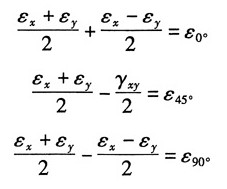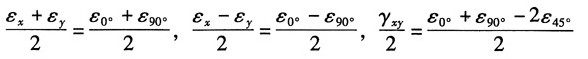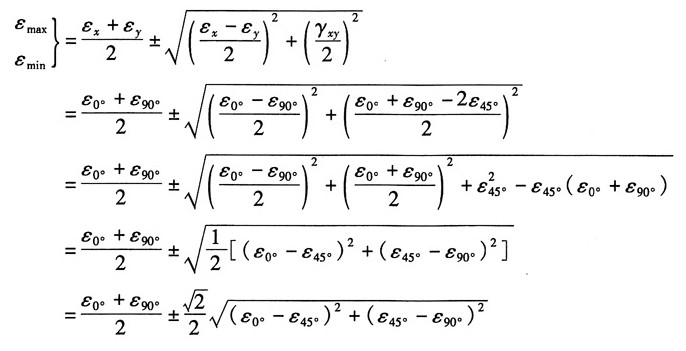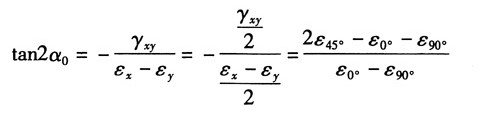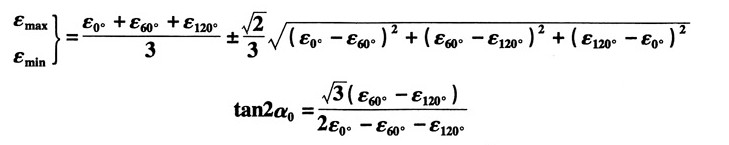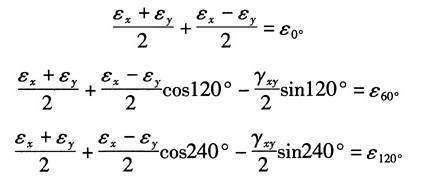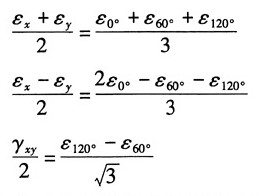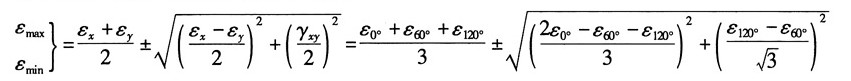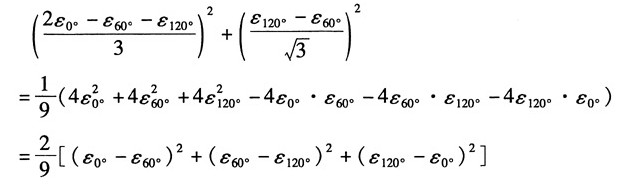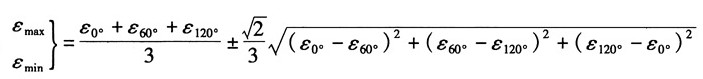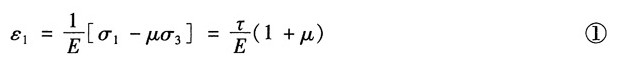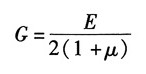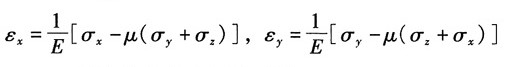计算题1. 构件受力如图1所示。
 图1
图1 (1)试确定危险点的位置。
(2)用单元体表示危险点处的应力状态。
解:(a)杆处于单向拉伸状态,每个点都是危险点,其应力状态如图2(a)所示。
 图2
图2 (b)对图1(b)作如下标记。
受扭圆轴处于单向应力状态,BC段的轴表面点是危险点,应力状态如图2(b)所示。
(c)受弯扭组合作用的轴,危险点位于固定端截面处最上和最下边缘,为二向应力状态,如图2(c)所示。
(d)受拉伸与扭转作用的轴,轴表面各点都为危险点,为二向应力状态,如图2(d)所示。
2. 在图1所示各单元体中,试用解析法和图解法求斜截面ab上的应力。应力的单位为MPa。
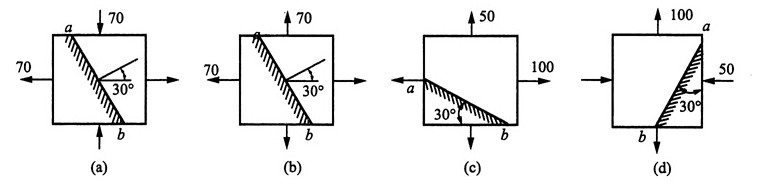 图1
图1
解:(1)①解析法
由图1(a)可知:σ
x=70MPa,σ
y=-70MPa,τ
xy=0,α=30°
则有:
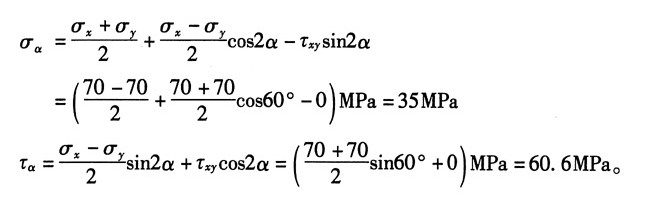
②图解法
作σOτ直角坐标系,A点(σ
x,τ
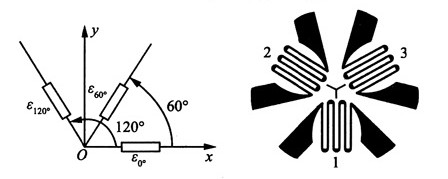
xy),B点(σ
y,-τ
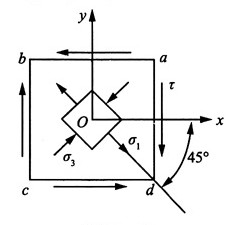
xy),以AB为直径作圆,即为应力圆,圆心为O,以OA为始边,逆时针旋转2α=60°与应力圆的交点(σ
C,τ
C)即为斜截面ab上的应力,如图2(a)所示,由图量取知:σ
α=σ
C=35MPa,τ
α=τ
C=61MPa
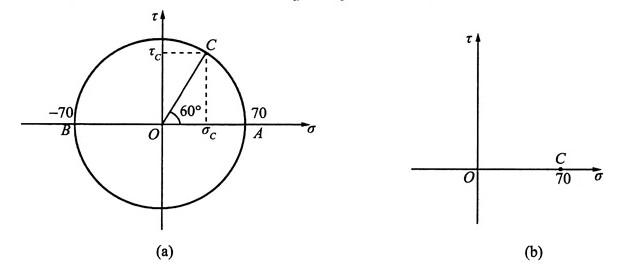
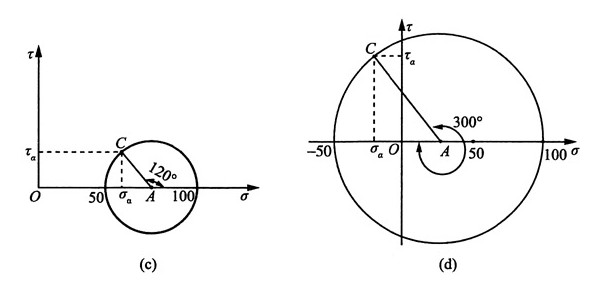 图2
图2 (2)①解析法
由图1(b)可知:σ
x=70MPa,σ
y=70MPa,τ
xy=0,α=30°
则有:
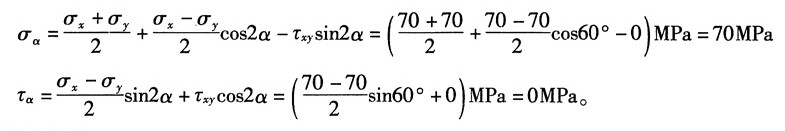
②图解法
同理,该单元体的应力圆褪化为一个点C(70,0),也称点圆,如图2(b)所示。故有σ
α=70MPa,τα=0MPa
(3)①解析法
由图1(c)知:σ
x=100MPa,σ
y=50MPa,τ
xy=0,α=60°
则有:
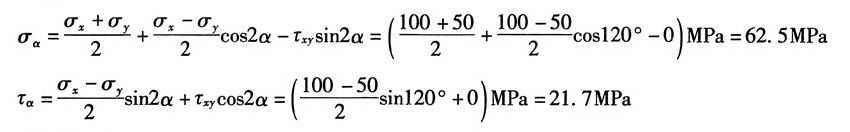
②图解法
同理,该单元体的应力圆如图2(c)所示。由图量取知:σ
α=σ
C=63MPa,τ
α=τ
C=22MPa。
(4)①解析法
由图1(d)可知:σ
x=-50MPa,σ
y=100MPa,τ
xy=0,α=150°
则有:
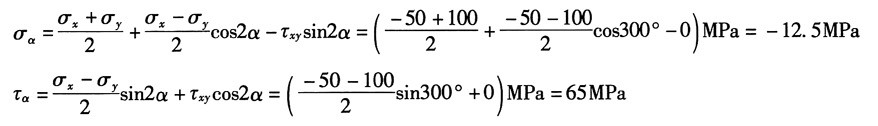
②图解法
同理,该单元体的应力圆如图2(d)所示。由图量取知:σ
α=-13MPa,τ
α=65MPa。
3. 已知单元体的应力状态如图1所示,图中应力单位皆为MPa。试用解析法及图解法求:
(1)主应力大小,主平面位置;
(2)在单元体上绘出主平面位置及主应力方向;
(3)图示平面内的极值切应力。
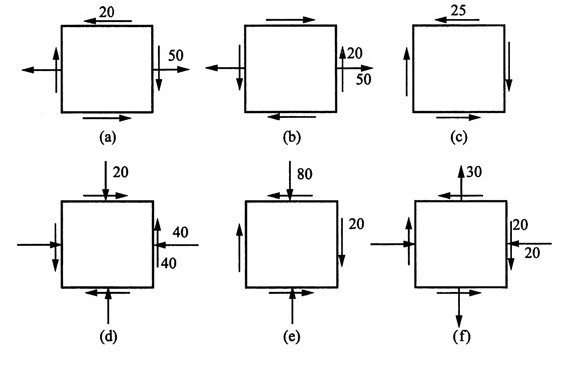 图1
图1
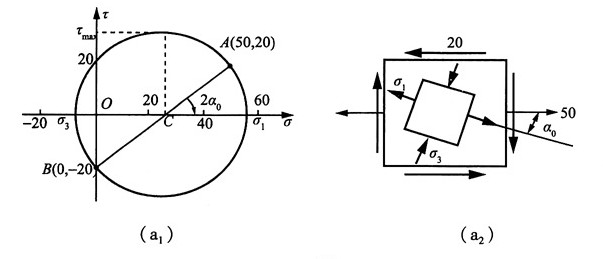
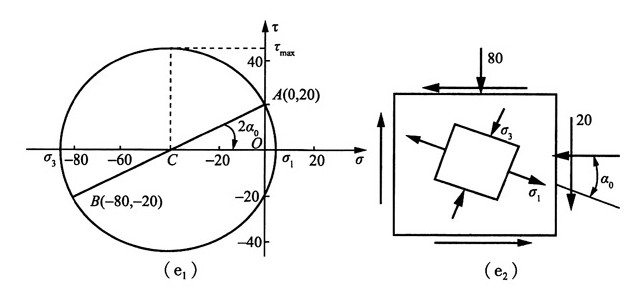
解:(1)图1(a),按应力的符号规则知:σ
x=5MPa,σ
y=0,τ
xy=20MPa
①解析法
由公式得:
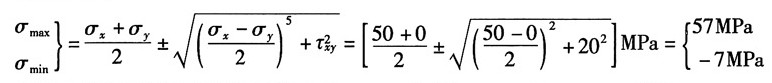
故按主应力的符号规定记主应力为:σ
1=57MPa,σ
2=0,σ
3=-7MPa
主平面位置:由
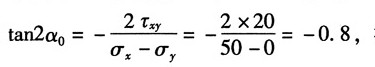
得α
0=-19.3°
最大切应力:

②图解法
作单元体的应力圆,如图2(a
1)所示,与σ轴的两个交点为σ
1、σ
3。应力圆的半径即为最大切应力的值,σ
1、σ
3、τ
max、2α
0均可从图上量取。
主平面在单元体上的位置是由已知x平面逆时针旋转α
0得到,如图2(a
2)所示。
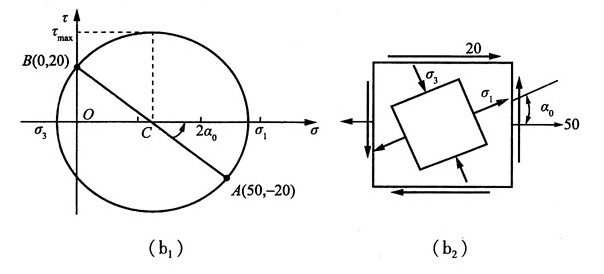
(2)图2(b),按应力的符号规则可知:σ
x=50MPa,σ
y=0,τ
xy=-20MPa
①解析法
由公式得:
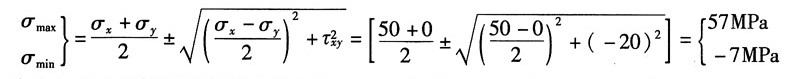
故按主应力的符号规定记主应力为:σ
1=57MPa,σ
2=0,σ
3=-7MPa
主平面位置:由
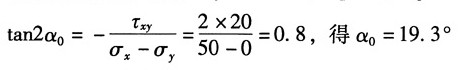
最大切应力:
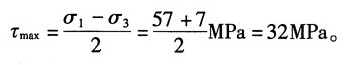
②图解法
作单元体的应力圆,如图2(b
1)所示σ
1、σ
3、τ
max、2α
0,均可从图上量取。主平面在单元体上的位置是由已知x平面逆时针旋转α
0得到,如图2(b
2)所示。
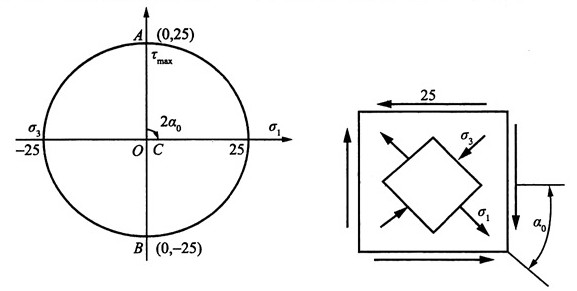
(3)图1(c),按应力的符号规则知:σ
x=0,σ
y=0,τ
xy=25MPa
①解析法
由公式得:
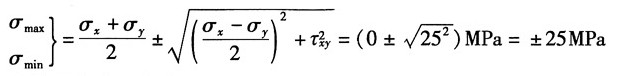
故按主应力的符号规定记主应力为:σ
1=25MPa,σ
2=0,σ
3=-25MPa
主平面位置:由

得α
0=-45°
最大切应力:
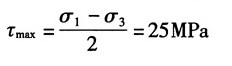
②图解法
作单元体的应力圆,如图2(c
1)所示,σ
1、σ
3、τ
max、2α
0均可从图上量取。
主平面在单元体上的位置是由已知x平面逆时针旋转α
0得到,如图2(c
2)所示。
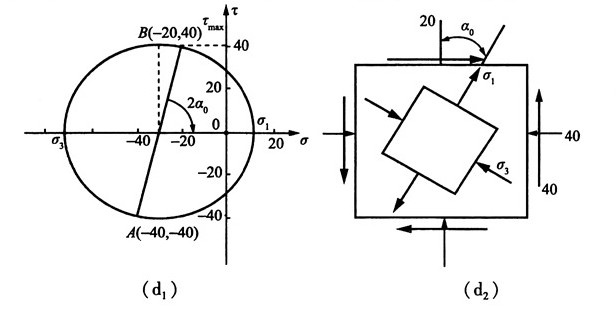
(4)图1(d),按应力的符号规则:σ
x=-40MPa,σ
y=-20MPa,τ
xy=-40MPa
①解析法
由公式得:
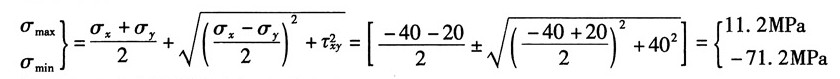
故按主应力的符号规定记主应力为:σ
1=1.12MPa,σ
2=0,σ
3=-71.2MPa
主平面位置:由

得α
0=-38°
最大切应力:
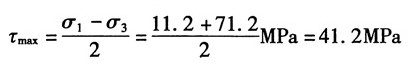
②图解法
作单元体的应力圆,如图2(d
1)所示,σ
1、σ
3、t
max、2α
0均可从图上量取。
主平面在单元体上的位置是由已知y平面逆时针旋转α
0得到,如图2(d
2)所示。
(5)图1(e),按应力的符号规则知:σ
x=0,σ
y=-80MPa,τ
xy=20MPa
①解析法
由公式得:
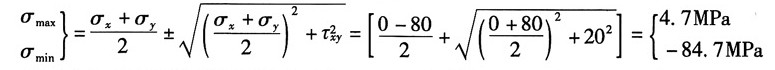
故按主应力的符号规定记主应力为:σ
1=4.7MPa,σ
2=0,σ
3=-84.7MPa
主平面位置由
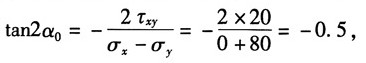
得α
0=-13.3°
最大切应力:
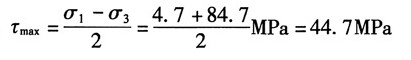
②图解法
作单元体的应力圆,如图2(e
1)所示,σ
1、σ
3、τ
max、2α
0均可从图上量取。
主平面在单元体上的位置是由已知x平面逆时针旋转α
0得到,如图2(e
2)所示。
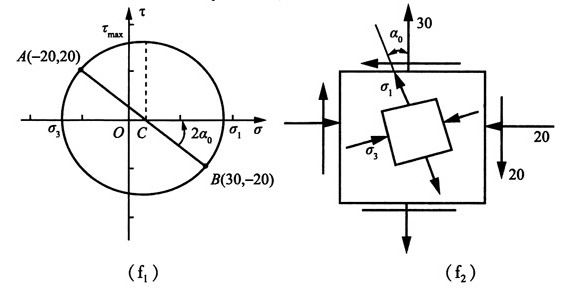
(6)图1(f),按应力的符号规则知:σ
x=-20MPa,σ
y=30MPa,τ
xy=20MPa
①解析法
由公式得:
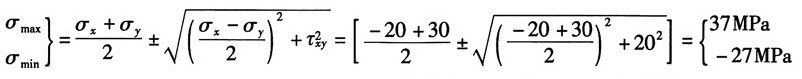
故按主应力的符号规定记主应力为:σ
1=37MPa,σ
2=0,σ
3=-27MPa
主平面位置由
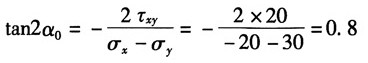
得:α
0=19.3°
最大切应力:
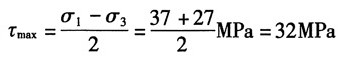
②图解法
作单元体的应力圆,如图2(f
1)所示,均可从图上量取。
主平面在单元体上的位置是由已知y平面逆时针旋转α
0得到,σ
1、σ
2、τ
max、2α
0如图2(f
2)所示。
4. 在图1所示应力状态中,试用解析法和图解法求出指定斜截面上的应力(应力单位为MPa)。
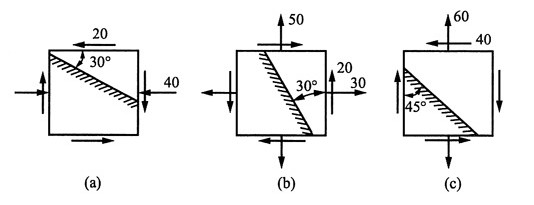 图1
图1
解:(1)①解析法
由图1(a)可知:σ
x=-40MPa,σ
y=0,τ
xy=20MPa,α=60°
则有:
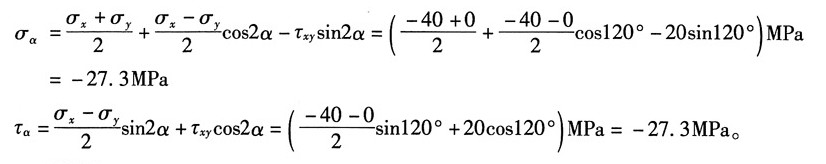
②图解法
作σOτ直角坐标系,A点(σ
x,τ
xy),B点(σ
y,-τ
xy),以AB为直径作圆,即为应力圆,记圆心为C,以CA为始边,逆时针旋转2α=120°与应力圆的交点即为所求斜截面上的应力(σ
α,τ
α),如图2(a)所示,由图量取得解。

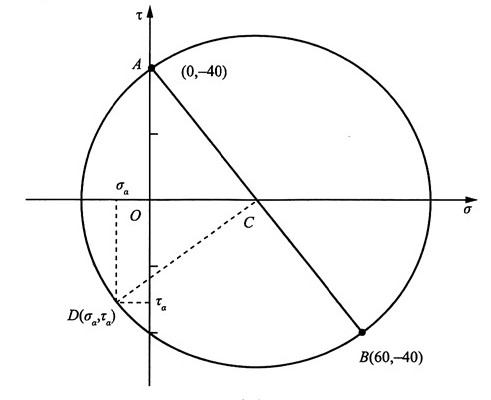 图2
图2 (2)①解析法
由图1(b)可知:σ
x=30MPa,σ
y=50MPa,τ
xy=-20MPa,α=30°
则有:
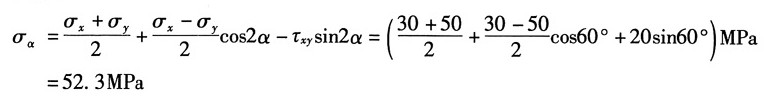
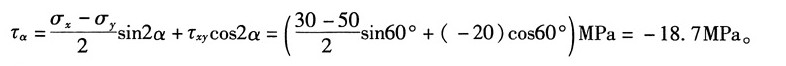
②图解法
同理作应力圆,以C为圆心,以CA为始边,逆时针旋转2α=60°与应力圆的交点即为所求斜截面上的应力(σ
α,τ
α),如图2(b)所示,由图量取得解。
(3)①解析法
由图1(c)可知:σ
x=0,σ
y=60MPa,τ
xy=40MPa,α=45°
则有:
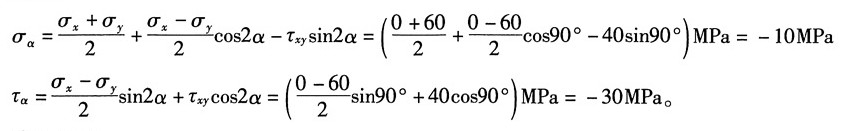
②图解法
同理作应力圆,以C为圆心,以CA为始边,逆时针旋转2α=90°与应力圆的交点即为所求斜截面上的应力(σ
α,τ
α),如图2(c)所示,由图量取得解。
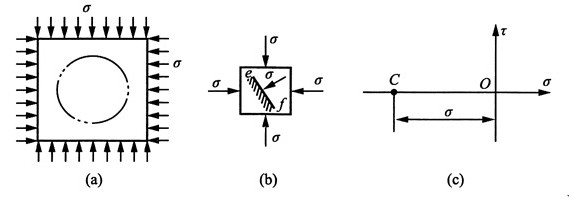
5. 若物体在两个方向上受力相同,如图(a)所示,试分析物体内任一点的应力状态。
解:在这种情况下,物体内任意一点的应力状态皆如图(b)所示。代表这一应力状态的应力圆如图(c)所示退缩成一点C,半径等于零。单元体任意斜面ef上的正应力都等于σ,切应力都等于零。这样,如从物体中任意地割取一部分,例如从中分割出一个圆柱体,则在圆柱体的柱面上的正应力也都是σ。
6. 圆筒壁内任意点处的主应力σ
1、σ
2及图示平面内的极值切应力τ
max;
解:根据题意,壁内单元体为二向应力状态,主应力分别为:
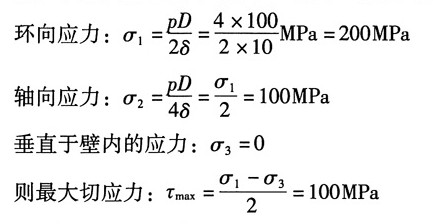
旷等=勰MPa=200MPa
7. 斜截面ab上的正应力及切应力。
解:由图可知:σ
x=100MPa,σ
y=200MPa,τ
xy=0,α=60°
根据公式得斜截面ab上的应力为:
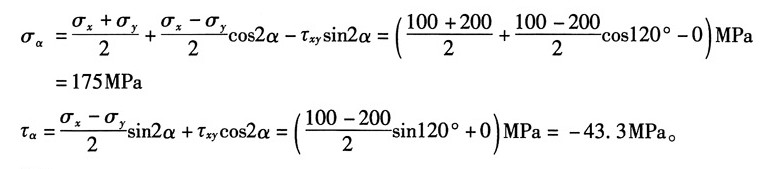
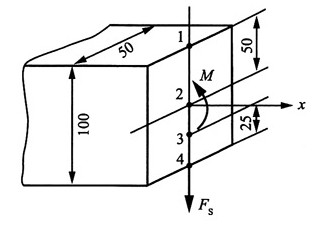
8. 已知矩形截面梁某截面上的弯矩及剪力分别为M=10kN·m,F
S=120kN,试绘出截面上1、2、3、4各点处的应力状态的单元体,并求其主应力。
解:(1)1点
其应力分量:
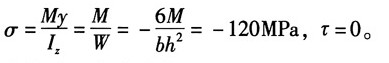
其处于单向应力状态,主应力为:σ
1=σ
2=0,σ
3=σ=-120MPa
应力状态如图(a)所示。
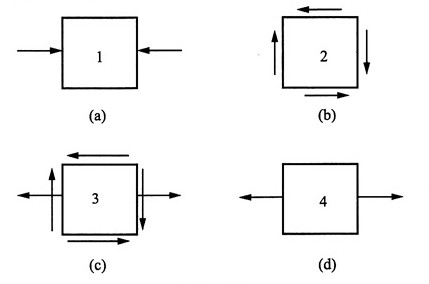
(2)2点
其应力分量:

其处于纯剪切状态,主应力为:σ
1=36MPa,σ
2=0,σ
3=-36MPa
应力状态如图(b)所示。
(3)3点
其应力分量:
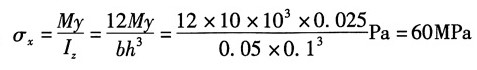
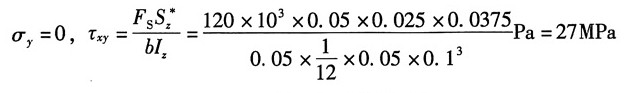
根据
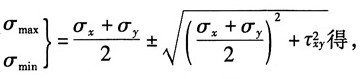
其主应力:
σ
1=70.4MPa,σ
2=0,σ
3=-10.4MPa
应力状态如图(c)所示。
(4)4点
同点1处于单向应力状态,但该点受拉,则主应力:σ
1=120MPa,σ
2=σ
3=0
应力状态如图(d)所示。
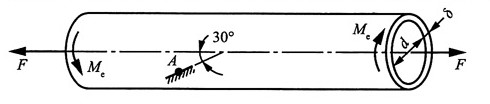
9. 钢制曲拐的横截面为圆形,其直径为20mm,C端与钢丝相连,钢丝的横截面面积A=6.5mm
2。曲拐和钢丝的弹性模量同为E=200GPa,G=84GPa。若钢丝的温度降低50℃,且α
l=12.5×10
-6℃
-1,试求曲拐截面A的顶点处的应力状态。
解:(1)求钢丝内力F
假想沿C点将该结构断开,则钢丝上C点的位移δ
C与曲拐ABC上C点的挠度δ'
C相等,即有变形协调方程:δ
C=δ'
C。
δ
C由两部分组成:温度降低使钢丝缩短Δl
T,在内力F作用下伸长Δl
F:
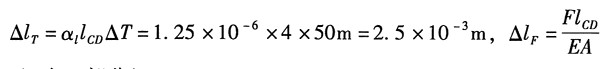
δ'
C由三部分组成:AB杆的弯曲变形产生的B端垂直位移w
B,BC杆的弯曲变形产生的C端垂直位移w
C,AB杆扭转引起的C端位移φ
Bl
BC。
故根据叠加原理可得:
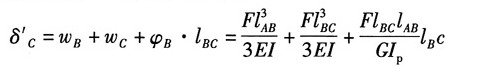
曲拐横截面对中性轴的惯性矩:
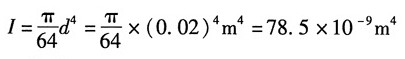
则其极惯性矩:I
p=2I=1.57×10
-8m
4 将以E各式代入协调方程可得:F=26.1N。
(2)求截面A顶点应力状态
由(1)可知曲拐截面A顶点的应力分量:
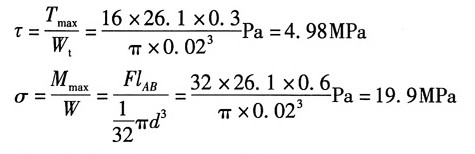
其应力状态如图所示。
10. A点在指定斜截面上的应力;
解:A的应力状态的单元体如图(a)所示,则:

对于薄壁圆筒其切应力:
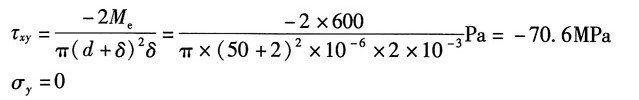
由公式得所求斜截面上的应力:
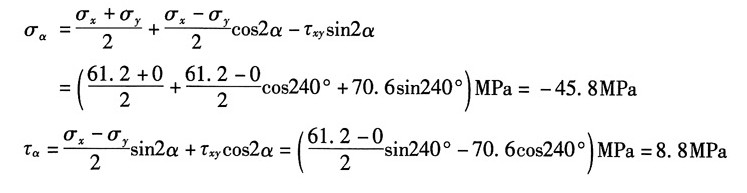
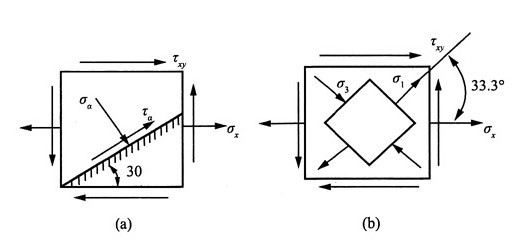
11. A点主应力的大小及方向(用单元体表示)。
解:A点的主应力:
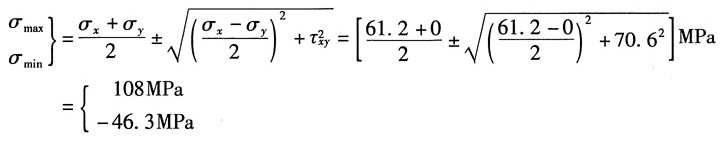
又根据符号规定得,A点的主应力:σ
1=108MPa,σ
2=0,σ
3=-46.3MPa
方向:由
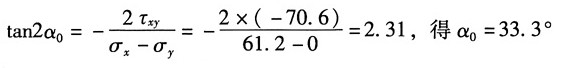
则其方位图如图(b)所示。
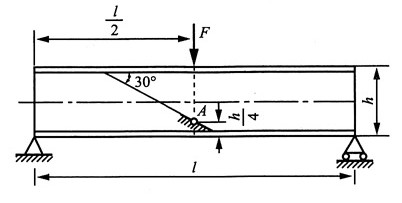
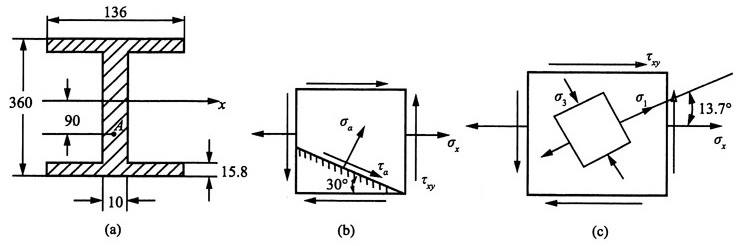
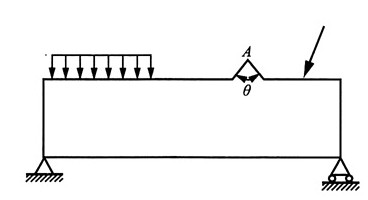
12. 如图所示简支梁为36a工字钢,F=140kN,l=4m。A点所在横截面在集中力F的左侧。且无限接近F力作用的截面。试求:
(1)A点在指定斜截面上的应力;
(2)A点的主应力及主平面位置(用单元体表示)。
解:根据题意,A点所在截面的内力分量分别为:

查型钢表知36a工字钢的截面参数I
x=15880cm
4,截面尺寸如图(a)所示。
由此可计算点A以下部分对中性轴的静矩:

分析可知,A点的应力状态单元体如图(b)所示。其中,应力分量:
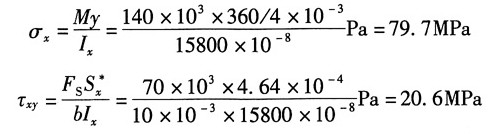
(1)根据公式可得所求斜截面上的应力:
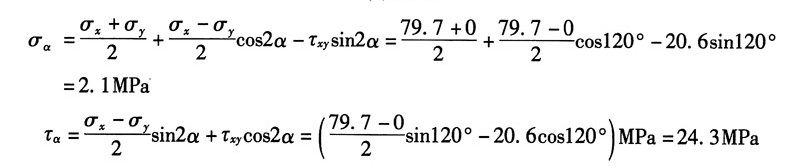
(2)A的点主应力:
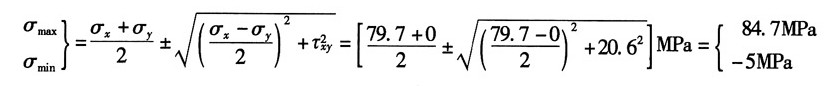
又根据符号规定得,A点的主应力:σ
1=84.7MPa,σ
2=0,σ3
=-5MPa
方向:由
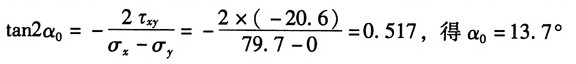
则其方位图如图(c)所示。
13. 二向应力状态如图1所示,应力单位为MPa。试求主应力并作应力圆。
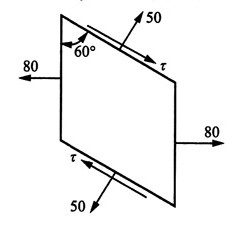 图1
图1
解:从图1中取出一个楔形单元体,如图2(a)所示。
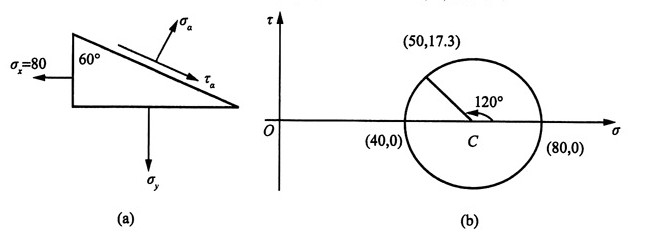 图2
图2 则根据应力符号规则有:σ
x=80MPa,τ
xy=0,σ
α=50MPa,α=60°
由公式:
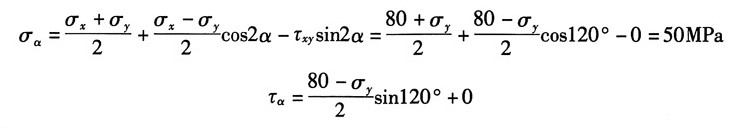
可得:σ
y=40MPa,τ
α=17.3MPa
绘制应力圆如图2(b)所示。
则单元体的主应力为:σ
1=80MPa,σ
2=40MPa,σ
3=0。
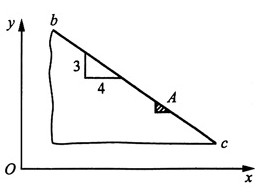
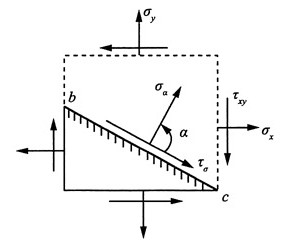
14. 在处于二向应力状态的物体的边界bc上,A点处的最大切应力为35MPa。试求A点的主应力。若在A点周围以垂直于x轴和y轴的平面分割出单元体。试求单元体各面上的应力分量。
解:(1)根据题意知,自由边界bc面上的剪应力和正应力均为零,因而是一个主平面,且其上的主应力为零,因此A点处于单向应力状态下,只有一个主应力不为零。此时A点主应力有两种可能:
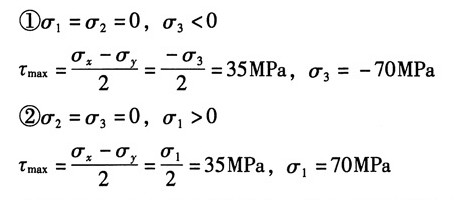
(2)若在A点周围以垂直于x轴和y轴的平面分割出单元体,其单元体如图所示,则有:
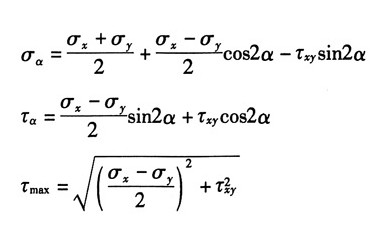
已知斜截面bc是边界自由表面,故σ
α=τ
α=0,其中由几何关系
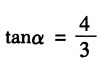
得:α=53.1°。
则该单元体上各面上的应力分量:
σ
x=-44.8MPa,σ
y=-25.2MPa,τ
xy=-33.6MPa
负号表示应力的真实方向与图所示方向相反。
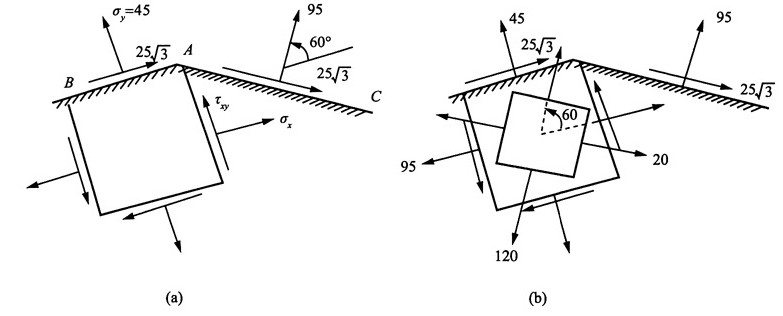
15. 在通过一点的两个平面上,应力如图所示,单位为MPa,试求主应力的大小及主平面的位置,并用单元体的草图表示出来。
解:选取如图(a)所单元体,则有:
由斜截面应力计算公式
得:σ
x=95MPa
由主应力计算公式得:
根据主应力标记符号规定,记主应力为:σ
1=120MPa,σ
2=20MPa,σ
3=0
主平面位置:由
综上,单元体主应力及其位置表示如图(b)所示。
16. 如图所示,以绕带焊接成的圆管,焊缝为螺旋线。管的内径为300mm,壁厚为1mm,内压p=0.6MPa。试求沿焊缝斜面上的正应力和切应力。
解:在焊缝斜面上一点取一单元体,如图所示。
分析可得该单元体上应力分量为:
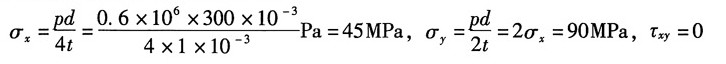
取焊缝截面外法线方向与x轴夹角α=-40°,则该截面上的正应力与切应力分别为:
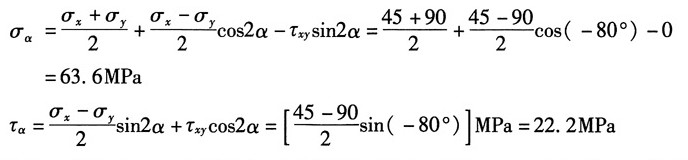
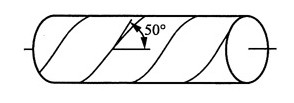
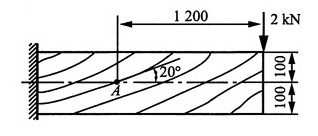
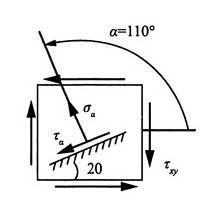
17. 如图所示,木质悬臂梁的横截面是高为200mm、宽为50mm的矩形。在A点,木材纤维与水平线的倾角为20°。试求通过A点沿纤维方向的斜面上的正应力和切应力。
解:取A点处的单元体,如图所示。由于A点在梁的中性轴上,因此处于纯剪切状态,则A点的应力分量:
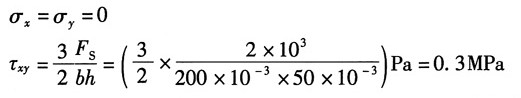
根据斜截面应力计算公式得α=110°,则A点所在的斜截面上的应力分量:
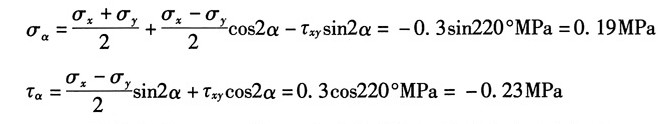
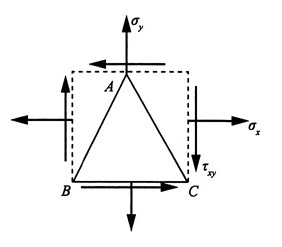
18. 板条如图所示。尖角的侧表面皆为自由表面,0<θ<π。试证明:尖角端点A处为零应力状态,即A点的主应力皆为零。
证明:取尖点A处的三角形单元体,如图所示。
已知AB、AC面为自由表面,故其应力为零。由三角形ABC单元体平衡方程可知,BC截面上的应力也为零。
故斜截面AB上的应力:
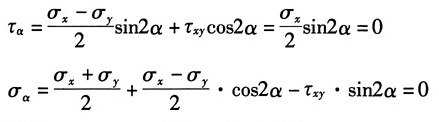
其中0<θ<π,sin2α≠0,所以σ
x=σ
y=τ
xy=0,A点为零应力状态。
命题得证。
19. 对二向应力状态,如图所示,表1中所列各题分别给出了某些应力分量(单位为MPa)或斜面的方位,试求表中空白处的未知量,并画单元体的草图,标明主应力的大小和σ
1所在主平面的方位(用外法线方向与x轴的夹角α来表示)。
| 表1 |
| 题号 | σx | σy | τxy | 斜面的方位和应力 | 主应力及主平面位置 | τmax |
| α | σα | τα | σ1 | σ2 | σ3 | σ1的方向 |
| 7.18(a) | 90 | | 0 | 15° | 80 | | | | | | |
| 7.18(b) | | | 40 | 30° | -20 | 20 | | | | | |
| 7.18(c) | 80 | | | | | | 100 | | | | 70 |
| 7.18(d) | 40 | | 60 | | | | | | -80 | | |
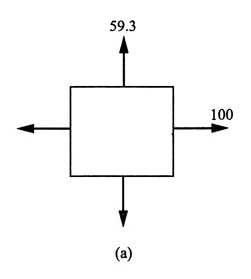
解:(a)已知σ
x=90MPa,τ
xy=0,α=15°,σ
α=80MPa
由斜截面应力计算公式得:
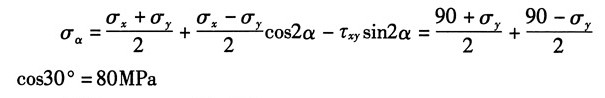
解得:σ
y=-59.3MPa
则斜截面上的切应力:
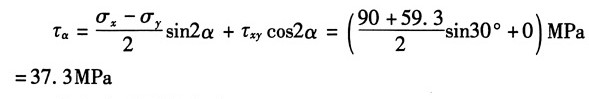
由主应力计算公式:
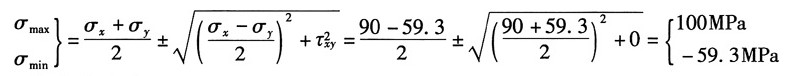
可得主应力为:σ
1=100MPa,σ
2=0,σ
3=-59.3MPa
主平面的方向:由
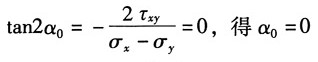
最大切应力:
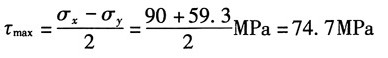
主应力和主平面在单元体上的表示如图(a)所示。
(b)已知τ
xy=40MPa,α=30°,σ
α=-20MPa,τ
α=20MPa
由斜截面应力计算公式得:
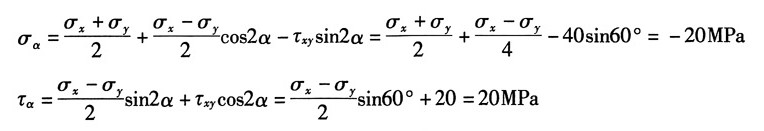
解得:σ
x=14.6MPa,σ
y=14.6MPa
由主应力计算公式:
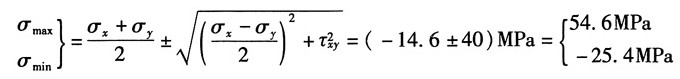
可得主应力为:σ
1=54.6MPa,σ
2=0MPa,σ
3=-25.4MPa
主平面的方向:由
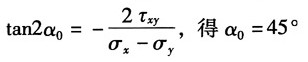
最大切应力:
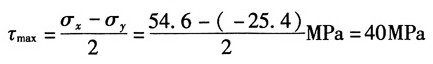
主应力和主平面在单元体上的表示如图(b)所示。
(c)已知σ
x=80MPa,σ
1=100MPa,τ
max=70MPa
由最大切应力计算公式
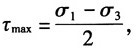
可得主应力:σ
3=-40MPa
因该单元体为二向应力状态,故其另一主应力:σ
2=0
由主应力计算公式得:
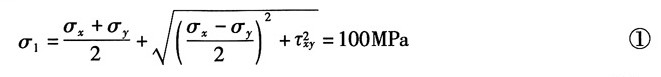
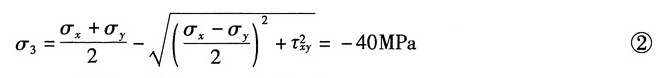
联立式①②得:σ
x+σ
y=60MPa,故有:σ
y=-20MPa
反代入式①计算得:τ
xy=±49MPa
主平面方向:由
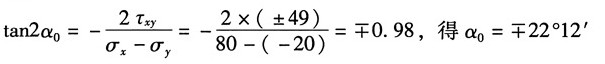
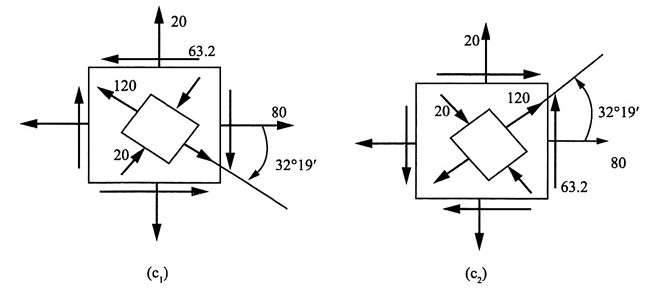
故其主平面单元体表示有两种情况,如图(c
1)(c
2)所示。
(d)已知σ
x=40MPa,τ
xy=60MPa,σ
3=-80MPa
由主应力计算公式得:
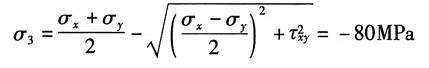
解得:σ
y=-50MPa
故有:
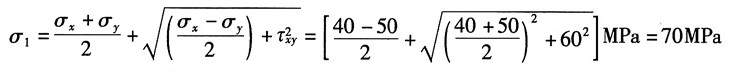
综上,主应力为:σ
1=70MPa,σ
2=0,σ
3=-50MPa
主平面方向:由
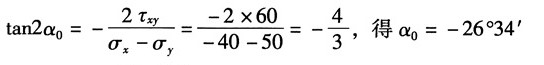
最大切应力:
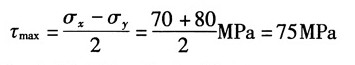
主应力和主平面在单元体上的表示如图(d)所示。
综上,最终表中未知量如表2所示。
| 表2
|
| 题号
|
σx
|
σy
|
τxy
|
斜面的方位和应力
|
主应力及主平面位置
|
τmax
|
| α
|
σα
|
τα
|
σ1
|
σ2
|
σ3
|
σ1的方向
|
| (a)
|
100
|
-59.3
|
0
|
15°
|
80
|
37.3
|
90
|
0
|
-59.3
|
0
|
74.7
|
| (b)
|
14.6
|
14.6
|
-40
|
30°
|
-20
|
20
|
54.6
|
0
|
-25.4
|
-45°
|
40
|
| (c)
|
80
|
-20
|
±49.0
|
|
|
|
120
|
0
|
-40
|
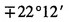
|
70
|
| (d)
|
40
|
-50
|
60
|
|
|
|
70
|
0
|
-80
|
-26°34'
|
75
|
20. 试求图1所示各应力状态的主应力及最大切应力(应力单位为MPa)。
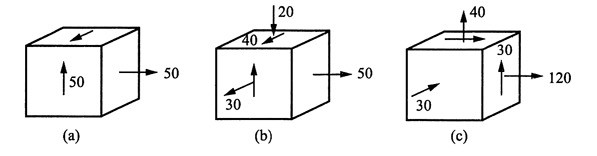 图1
图1
解:对图1分别建立如图2所示坐标系。
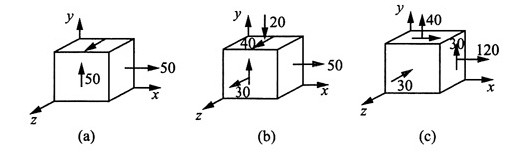 图2
图2 (a)已知σ
x=50MPa,σ
y=σ
z=0,τ
yz=50MPa,其中σ
x=50MPa为主应力。
又根据主应力计算公式:
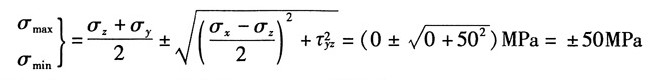
可得主应力为:σ
1=σ
2=50MPa,σ
3=-50MPa
故最大切应力为:
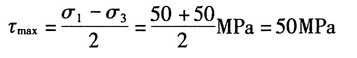
(b)已知σ
x=50MPa,σ
y=-20MPa,σ
z=30MPa,τ
yz=40MPa,其中σ
x=50MPa为主应力。
又根据主应力计算公式:
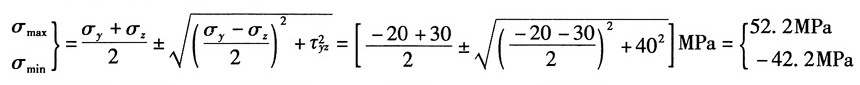
可得主应力为:σ
1=52.2MPa,σ
2=50MPa,σ
3=-42.2MPa
故最大切应力为:
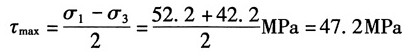
(c)已知σ
x=120MPa,σ
y=40MPa,σ
z=-30MPa,τ
xy=-30NPa,其中σ
z=-30MPa为主应力。
又根据主应力计算公式:
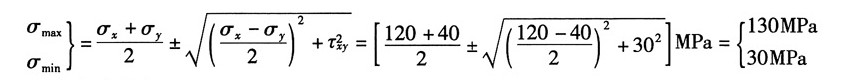
可得主应力为:σ
1=130MPa,σ
2=30MPa,σ
3=-30MPa
故最大切应力为:

21. 已知:
(a)ε
x=-0.00012,ε
y=0.00100,γ
xy=0.00020
(b)ε
x=0.00060,ε
y=-0.00020,γ
xy=-0.00080
试求主应变及其方向。
解:(a)根据主应变计算公式:
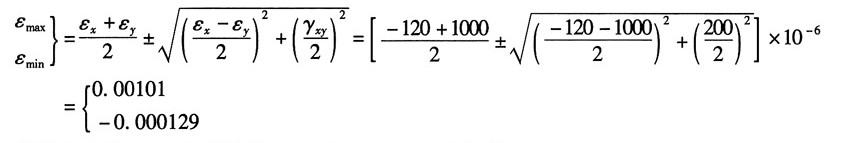
则主应变为:ε
1=0.00101,ε
2=0,ε
3=-0.000129
方向:
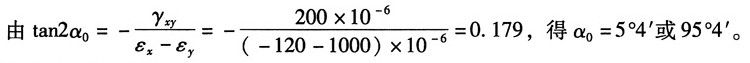
(b)根据主应变计算公式:

则主应变为:ε
1=0.00077,ε
2=0,ε
3=-0.00037
方向:
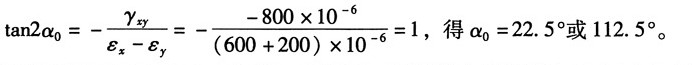
22. 在直角应变花的情况下,如图所示,试证明主应变的数值及方向可用以下公式计算:
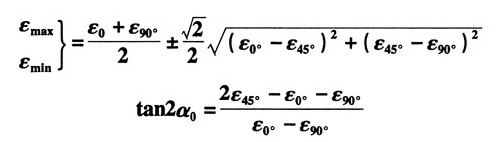
证明:根据任意方向的应变公式:
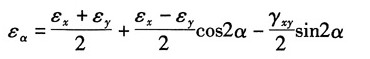
令α=0°,α=45°,α=90°得:
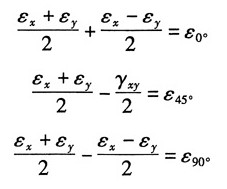
联立以上三式,解得:
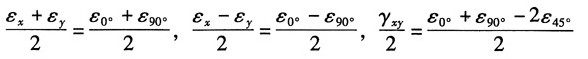
由主应变公式得:
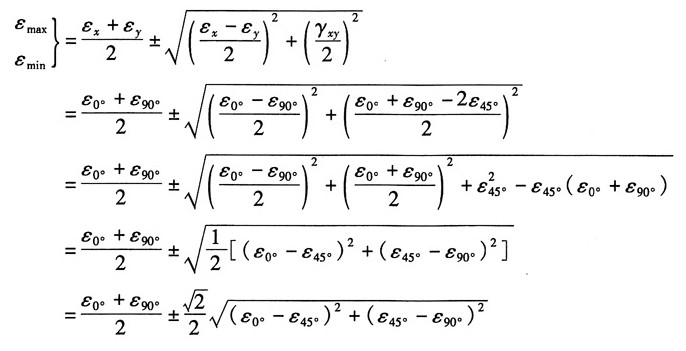
主应变方向角:
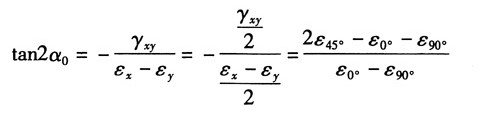
命题得证。
23. 等角应变花如图所示。三个应变片的角度分别为:α
1=0°,α
2=60°,α
3=120°。试证明主应变的数值及方向可由以下公式计算:
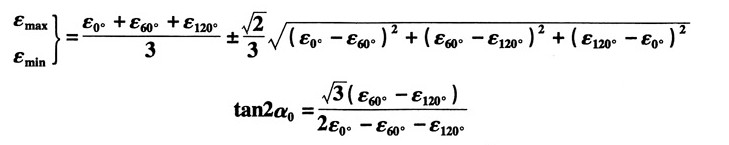
证明:根据任意方向的应变公式,分别令α=0°,α=60°,α=120°得:
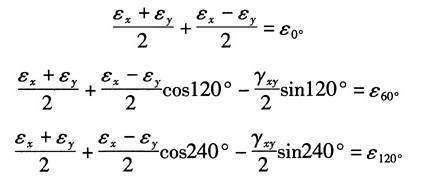
解得:
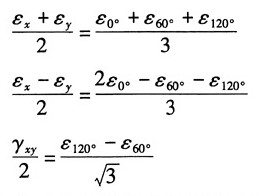
将以上各式代入主应变计算公式得:
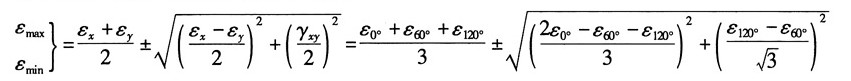
整理根号内部分:
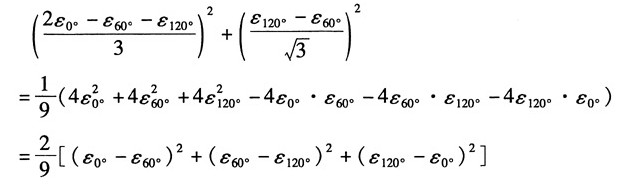
故主应变为:
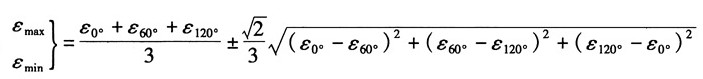
主应变方向为:

命题得证。
24. 用广义胡克定律。证明弹性常数E,G,μ间的关系。
证明:纯剪切状态的单元体如图所示,其主应力σ
1和σ
3分别在α
0=-45°和α
0=-135°的主平面上,且σ
1=-σ
3=τ,σ
2=0。
将主应力代入由主应力表达的广义胡克定律得,主应变为
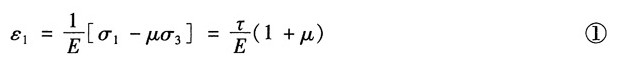
纯剪切应力状态下
据此,应用广义胡克定律得到:
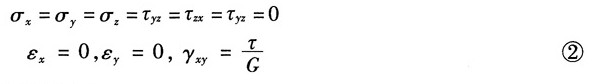
将②式代入任意方向上的正应变公式
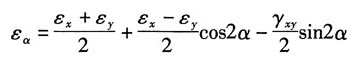
求得主应变

对比式①和式③,得
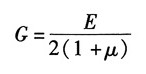
命题得证。
25. 列车通过钢桥时,在钢桥横梁的A点用变形仪量得ε
x=0.0004,ε
y=-0.00012。试求A点在x-x及y-y方向的正应力。设E=200GPa,μ=0.3。并问据此能否求出A点主应力?
解:由广义胡克定律可得:
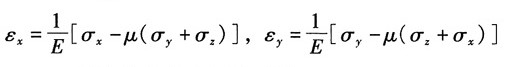
根据题意σz=0,将ε
x、ε
y、E、μ的值代入以上两式可得:
200×10
9×0.0004=σ
x-0.3σ
y 200×10
9×(-0.00012)=σ
y-0.3σ
x 解得:σ
x=80MPa,σ
y=0
由于在A点的单元体的切应力τ
xy未知,因此不能求出主应力。



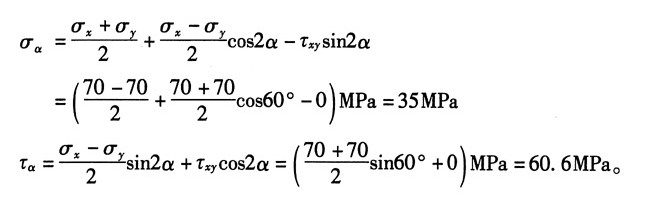


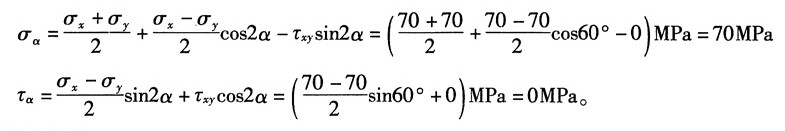
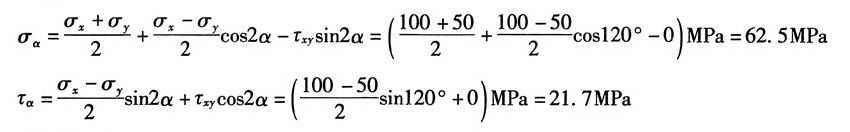
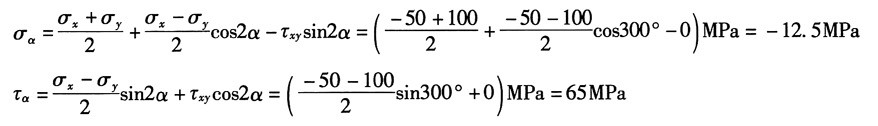

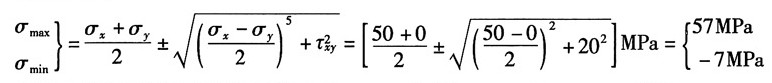
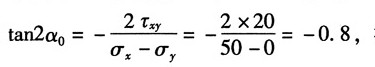 得α0=-19.3°
得α0=-19.3°
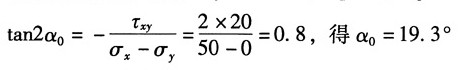
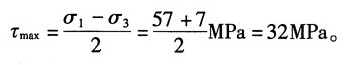
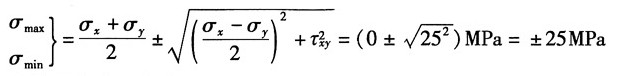
 得α0=-45°
得α0=-45°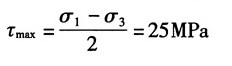
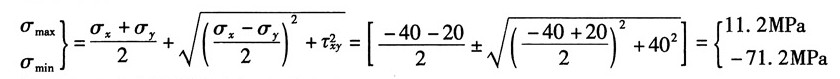
 得α0=-38°
得α0=-38°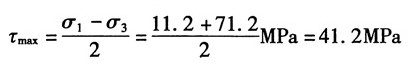
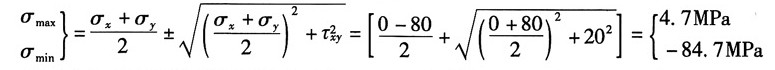
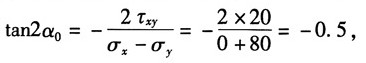 得α0=-13.3°
得α0=-13.3°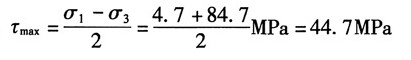
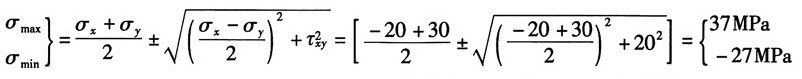
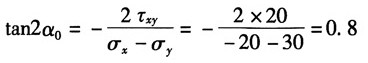 得:α0=19.3°
得:α0=19.3°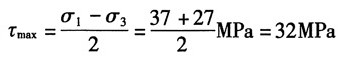

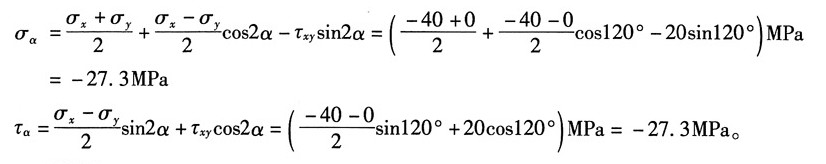


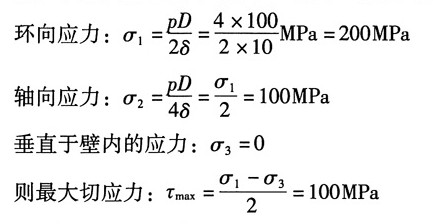 旷等=勰MPa=200MPa
旷等=勰MPa=200MPa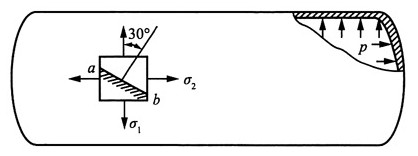
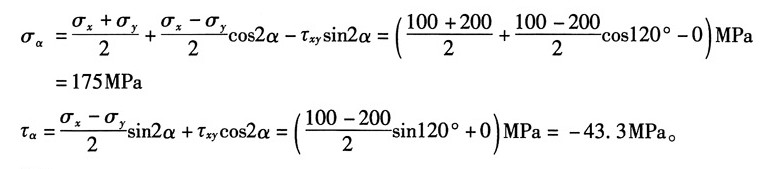
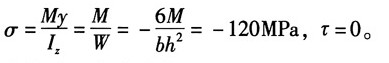

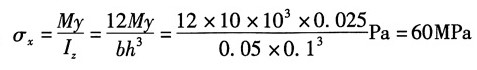
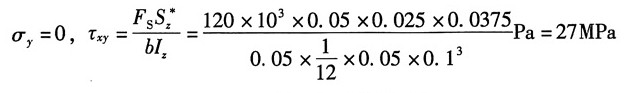
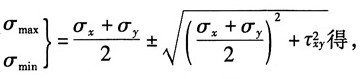 其主应力:
其主应力: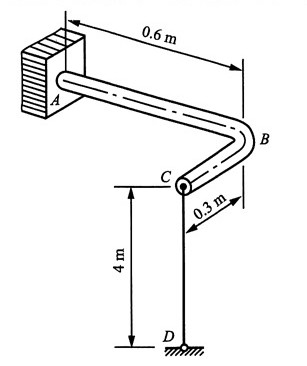
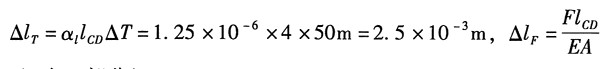
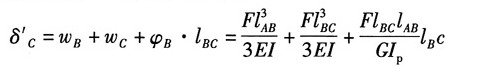
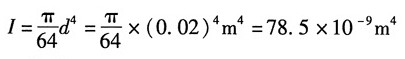
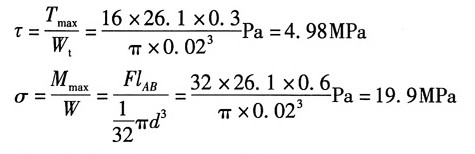

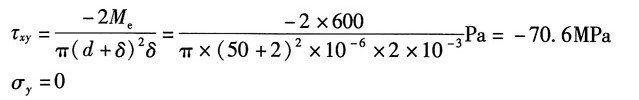
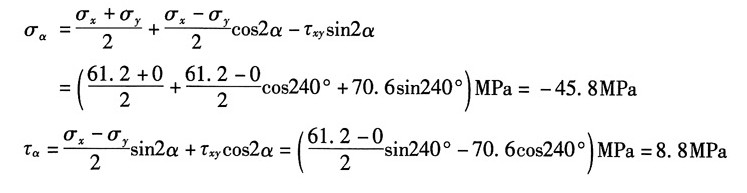
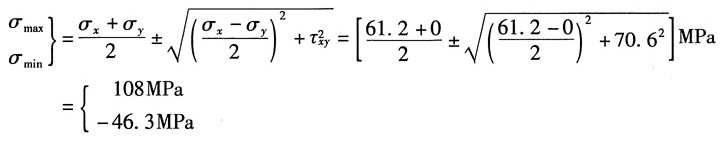
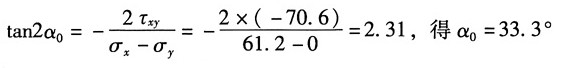


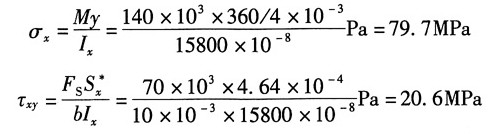
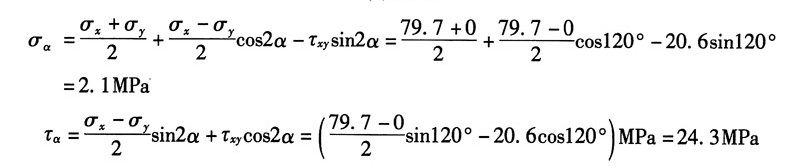
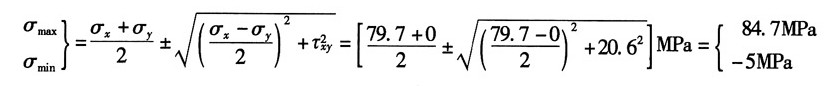
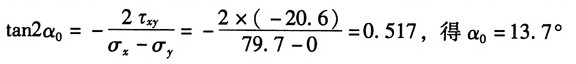


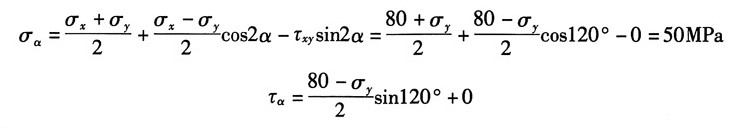
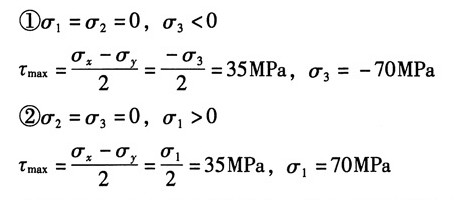
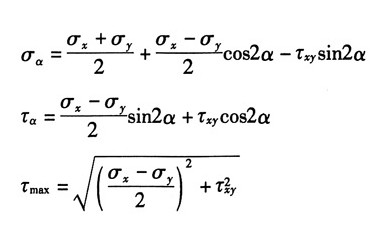
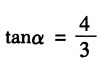 得:α=53.1°。
得:α=53.1°。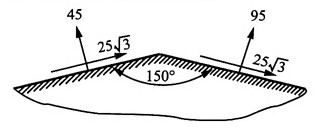
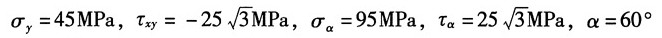
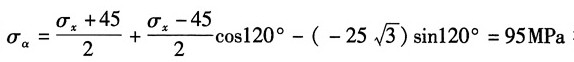 得:σx=95MPa
得:σx=95MPa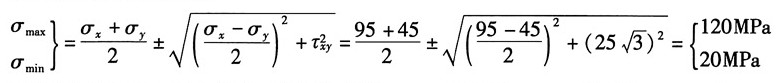
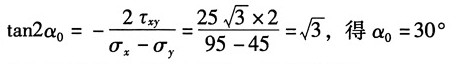

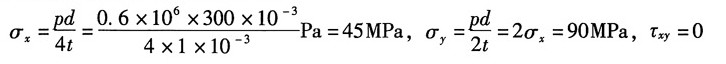
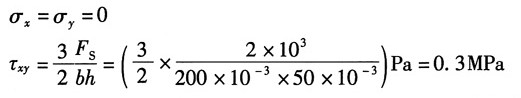
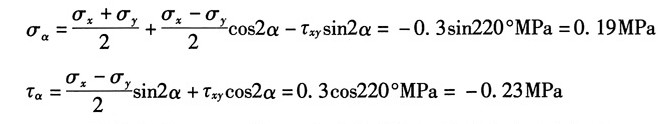
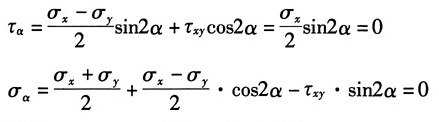
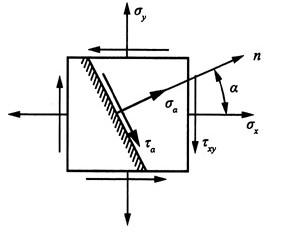
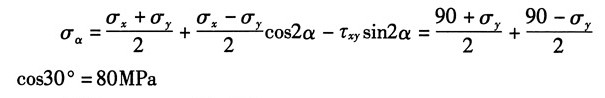
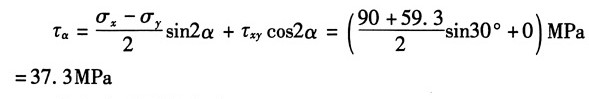
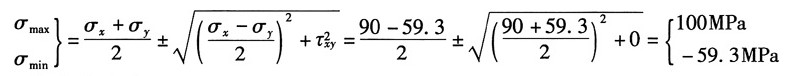
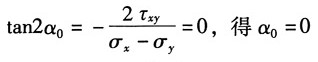
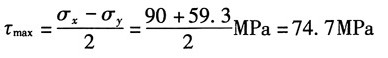
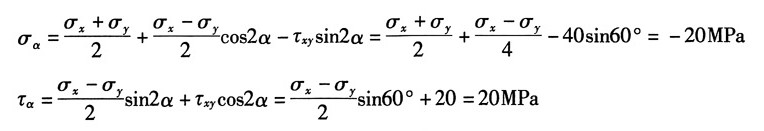
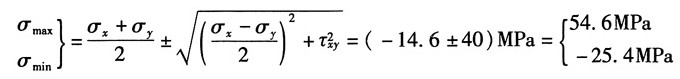
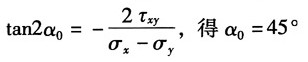
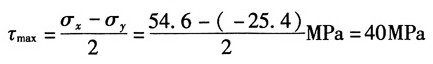

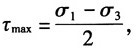 可得主应力:σ3=-40MPa
可得主应力:σ3=-40MPa