第Ⅰ部分 (选择题)
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)2. 下列函数中,在x=0处可导的是______
A.y=|x|
B.
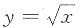
C.y=x
2 D.y=lnx
A B C D
C
[考点] 函数在一点处可导.
[解析] 选项A中,y=|x|在x=0处有尖点,即y=|x|在x=0处不可导;选项B中,
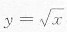
,

在x=0处不存在,即
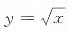
在x=0处不可导;选项C中,y=x
2,y'=2x处处存在,即y=x
2处处可导,也就在x=0处可导;选项D中,y=lnx,
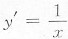
在x=0处不存在,y=lnx在x=0处不可导(事实上,y=lnx在x=0点就没定义).
3. 设y=xlnx-x,则y〞=______
A.

B.
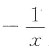
C.lnx
D.-lnx
A B C D
A
[考点] 一元函数的高阶导数.
[解析] y=xlnx-s,则y'=lnx+
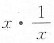
-1=lnx,
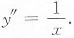
5. 设
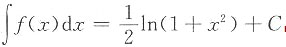
,则
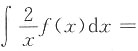
______
A.2arctanx+C
B.2arecotx+C
C.

D.
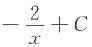
A B C D
A
[考点] 不定积分的计算.
[解析] 因为
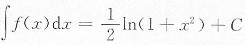
,则
所以
6. 设z=9tanx
2+5y,则
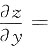
______
- A.18xarctanx2
- B.18xtanx2+5
- C.5
- D.18xcos2x
A B C D
C
[考点] 二元函数的偏导数.
[解析] z=9tanx
2+5y,则
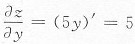
.
7.
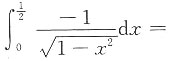
______
A.
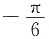
B.
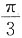
C.
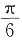
D.
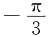
A B C D
A
[考点] 定积分的计算.
[解析]
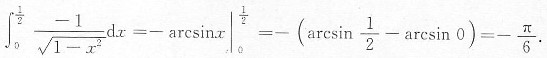
9. 设积分区域D由直线y=x,y=0,x=2围成,则
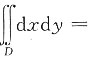
______
A.
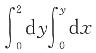
B.
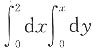
C.
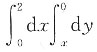
D.
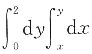
A B C D
B
[考点] 二重积分的计算.
[解析] 积分区域D={(x,y)|0≤x≤2,0≤y≤x}={(x,y)J 0≤y≤2,y≤x≤2),
所以
第Ⅱ部分 (非选择题)
二、填空题1.
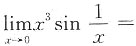
______.
0
[考点] 无穷小量的性质.
[解析]
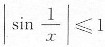
,则
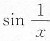
为有界量;
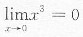
,则x
3为无穷小量,因为无穷小量与有界量的积为无穷小量,所以
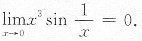
2. 函数y=x
6-6x+5在区间[ 1,5]上的最小值是______.
0
[考点] 函数的最值问题.
[解析] y'=6x5-6=6(x5-1),当x∈[1,5]时,y'≥0,所以y在区间[1,5]上为增函数,因此最小值为y(1)=1-6+5=0.
3. 若
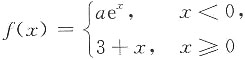
在x=0处连续,则a=______.
3
[考点] 分段函数在一点处连续.
[解析]
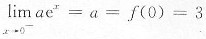
,所以a=3.
4.
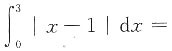
______.
[考点] 定积分的计算.
[解析]
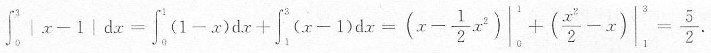
5.
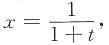
,y=2t
3,则

______.
-6t2(1+t)2
[考点] 由参数方程确定的函数的导数.
[解析]
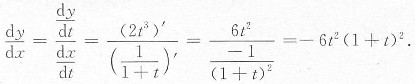
6. 已知平面π:3x+y-3z+2=0,则过原点且与π垂直的直线方程为______.
[考点] 空间直线的标准方程.
[解析] 已知平面π:3x+y-3z+2=0,其法向量n={3,1,-3}.又知直线与平面π垂直,则直线的方向向量为s={3,1,-3},所以直线方程为
7. 级数
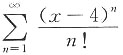
的收敛区间为______.
(-∞,+∞)
[考点] 幂级数收敛半径的求法.
[解析] 因为
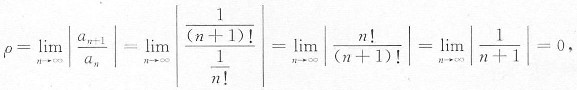
所以R=+∞,即收敛区间为(-∞,+∞).
8. 设区域D为x
2+y
2=1所围成的区域,则
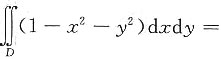
______.
[考点] 用极坐标变换来求二重积分.
[解析] 令r=rcosθ,y=rsinθ,所以
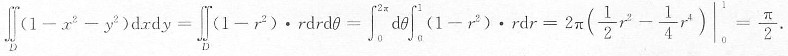
9. 微分方程y〞-3y'=0的特征方程是______.
r2-3r=0
[考点] 二阶常系数线性微分方程的特征方程.
[解析] 微分方程y〞-3y'=0的特征方程是r2-3r=0.
10. 设二元函数z=arcsin(xy),则
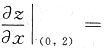
______.
2
[考点] 二元函数的偏导数.
[解析]
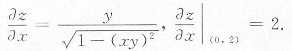
三、解答题(共70分。解答应写出推理、演算步骤)1. 计算
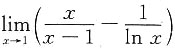
.
解:原式=
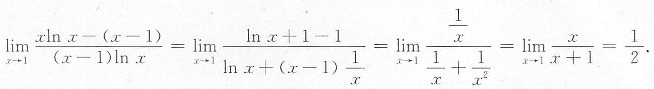
[考点] 洛必达法则.
2. 设f(x)=
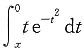
,求f(x)在[1,3]上的最大值.
解:因为f'(x)=-xe
-x2,所以f(x)在[1,3]上单调递减,所以它的最大值是f(1),而
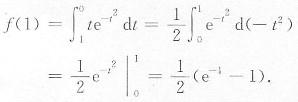
[考点] 函数的单调性.
3. 已知曲线y=ax
4+bx
3+x
2+4在点(1,6)处与直线y=11x-5相切,求a,b.
解:曲线过点(1,6).即点(1,6)满足曲线方程,
所以6=a+b+5,
①
再y'=4ax
3+3bx
2+2x,且曲线在点(1,6)处与y=11x-5相切,
所以
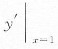
=4a+3b+2=11,②
联立①②解得a=6,b=-5.
[考点] 雨数导数的几何意义.
4. 求
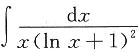
.
解:原式=
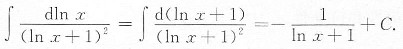
[考点] 不定积分的计算.
5. 求y〞+6y'+13y=0的通解.
解:特征方程为r
2+6r+13=0.故r=-3±2i为共轭复根,于是通解为
y=e-3x(C1cos2x+C2sin2x)
[考点] 二阶常系数齐次线性微分方程的求解.
6. 将函数
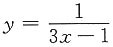
展开成x的幂级数,并指出其收敛区间.
解:因为
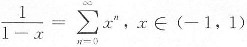
,所以
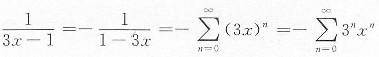
,
其中3x∈(-1,1),即x∈(
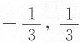
).
所以收敛区间为(
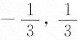
).
[考点] 函数幂级数的展开.
7. 计算二重积分
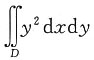
,
其中D为曲线x=y
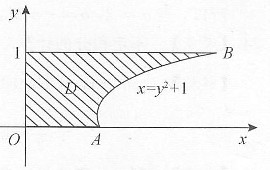
2+1,直线x=0,y=0,y=1所围成的区域.
解:如下图所示,积分区域D={(x,y)|0≤y≤1,0≤x≤y
2+1},所以
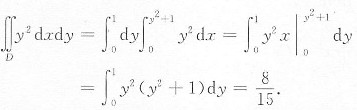
[考点] 二重积分的计算.
8. 求由曲线y=3-x
2,y=2x(x>0)与y轴所围成的平面图形的面积S,以及该封闭图形绕x轴旋转一周所成旋转体的体积V
x.
解:所给曲线围成的平面图形如下图所示,记为D.
由
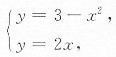
解得
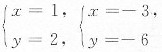
(舍掉).

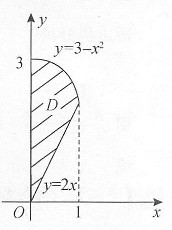
[考点] 用定积分求平面图形的面积公式和旋转体的体积公式.