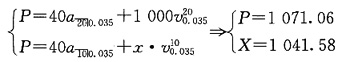计算题1. 一笔贷款在n年内分期偿还,每年末的偿还金额为X元,n>5,且
已知:
(1)第1期付款的利息金额为604.00元。
(2)第3期付款的利息金额为593.75元。
(3)第5期付款的利息金额为582.45元。
试计算X。
设贷款额为L,则

第t次付款的利息部分为X(1-v
n-t+1)
故X(1-v
n)=604.00,X(1-v
n-2)=593.75,X(1-v
n-4)=582.45
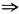
X=704.06元
2. 一笔35年期的贷款以等额分期方式偿还,每年末偿还一次。第8次分期付款的利息金额为135元。第22次分期付款的利息金额为108元。请计算第29次分期付款的利息金额。
设每年的等额分期付款金额为R,由已知
R(1-v
28)=135,R(1-v
14)=108
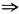
v
14=0.25,R=144
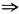
R(1-v
7)=144(1-0.5)=72
3. 一笔10000元的30年期贷款,年实际利率为5%,以等额分期方式偿还,每年末偿还一次。试求分期付款中利息金额最接近于付款金额1/3的年份。
第t年的分期付款中的利息金额为R(1-v
30-t+1)

故在第23年分期付款中利息金额最接近于付款金额的1/3。
4. 一笔10年期的贷款,在每年末偿还R元。已知:
(1)在头3年中,偿还的本金金额总和为290.35元。
(2)在最后3年中,偿还的本金金额总和为408.55元。
请计算在整个偿还期内,支付的利息金额为多少。
设贷款总额为L,则
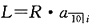
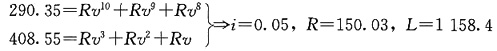
支付的利息金额总数为10R-L=341.76
5. 按年实际利率i偿还一笔1000元的贷款。已知:
(1)在第6年末偿还第一笔款项。
(2)然后每年末等额偿还一次,在第15年末可以偿清这笔贷款(即一共偿还10次)。
(3)在第10年末的付款结束后,未偿还本金余额为908.91元。
试计算第5年末的未偿还本金余额。
设等额年度付款金额为R:
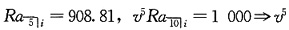
=0.661989
故第5年末的未偿还本金为
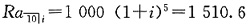
6. 借款人第2年末向偿债基金的储蓄额
借款人第2年末向偿债基金的储蓄额应为
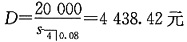
7. 偿债基金在第2年末的余额
第2年末的余额为
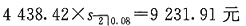
9. 有两笔贷款的本金均为20000元,期限均为4年,但偿还方式不同。第一笔贷款采用偿债基金方式,贷款利率为8%,偿债基金利率为7%。第二笔贷款采用等额分期偿还方式。试计算当第二笔贷款的利率为多少时,两笔贷款对借款人而言是等价的。
对于偿债基金,各年末的储蓄额为
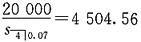
元,各年应支付的利息为20000×8%=1600。故每期总的支付金额为6104.56元
如果两笔贷款对借款人而言是等价的,则各期支付的金额应该相等,故
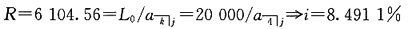
10. 一笔10年期的贷款在每年末偿还一次,年贷款利率为5%。第一次的付款为200元,后来的每笔付款均比前一年多10元。请计算第5次付款的利息是多少。
第4次付款后的未偿还金额为:

故第5次付款的利息部分为I=L
4·i=66.89
11. 一笔125000元的30年期贷款在每月末偿还一次,每年的月偿还金额相等。每一年的月偿还额较前一年高出2%。第一年的月偿还额为R元,年实际利率为5%,求R。
125000=
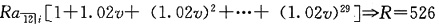
12. 银行有一笔10000元的20年期贷款,该笔贷款在每年末偿还1000元。如果银行把每次的偿还额立即按5%的实际利率进行再投资,试确定银行在这20年的实际年收益率。
各期还款的积累值为
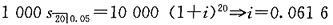
13. 某人有一笔55000的抵押贷款,每月末需偿还500.38,共需偿还n年。每月复利一次的年名义利率为i。借款人因故没有偿还第一期付款,但其余各笔均按时偿还了。由于没有偿还第一期付款,故在第n年末还欠3077.94。试计算利率i。
令月实际利率j=i/12
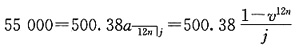
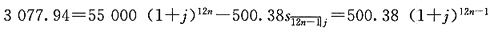
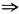
=12,j=0.0917
14. 某人自2000年1月1日起以年实际利率5%偿还一笔20000元的30年期贷款,每年末偿还一次。该人自2010年1月1日起又以年实际利率7%偿还另一笔10000元的20年期贷款,也在每年末偿还一次。试计算在2010年偿还的两笔贷款的本金之和。
第一笔贷款,每期偿还额
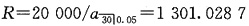
第11年内偿还的本金金额为P
11=Rv
30-11+1=490.3440
第二笔贷款
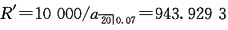
,P'
1=R'v
20-1+1=243.9293
故2010年一年内偿还的两笔贷款的本金之和为734.2733元。
15. 一笔50000的贷款分10次按年偿还。第一笔付款X在贷款后6个月末支付,以后每隔一年偿还一次,每次的偿还金额均为2X。假设前4.5年的年实际利率是5%,随后变为3%。试计算X。
将还款额分成3部分,一部分是0.5年的第一笔付款X;第二部分是自1.5年开始,支付4次,每次支付2X;第三部分是自5.5年开始,支付5次,每次支付2X,故有
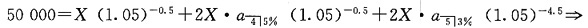
X=3278
16. 一笔1000元的贷款将以每月复利一次的名义利率12%计息,在6个月内的每月末分期偿还。前三次每次支付X,后三次每次支付3X。试求第三次支付的本金金额与第五次支付的利息金额。
由已知
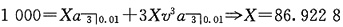
由过去法,第2期后未偿还本金金额为
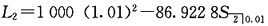
=845.3852
故第3次支付的本金金额为P
3=X=0.01L
2=78.4689
由将来法,第4期后未偿还本金金额为
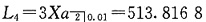
故第5次支付的利息金额为I
5=0.01L
4=5.1382
17. 一笔1000000元的30年期贷款将按月等额偿还,每月末偿还一次,每月复利一次的名义利率为X%。在第69期的还款额中,利息金额占94.473%,在第70期的还款额中,利息金额占94.418%。试求X。
第69期还款额中本金金额为P
69=Rv
360+1-69=Rv
292 故由已知
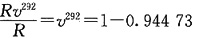
解得X=12(v
-1-1)=0.1196
另一种解法:由于等额分期偿还中各期还款中的本金金额为P
k=Rv
n-k+1,故第69期和70期偿还的本金金额比为Pc
/P
70=v
-1=1+X/12=(1-94.473%)/(1-94.418%)
同样解得X=0.1196
18. 一笔1000元的30年期贷款按年分期偿还,每年末偿还一次,年实际利率为8%。前10期的偿还金额均等于应付利息,第11至20期的偿还金额等于应付利息的两倍,后10期的偿还金额等于X。试求X的值。
10年末的未偿还贷款余额仍为1000元
第11至20次付款等于应付利息的2倍,即本金偿还值等于应付利息值,有I
11=0.08L
10 L
11=L
10-P
11=L
10-I
11=0.92L
10 L
12=0.92L
11-(0.92)
2L
10 ……
L
20=(0.92)
10L
10=(0.92)
10(1000)=434.3885
后10期每期付款等于X,故L
20=434.3885=
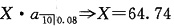
19. 一笔15年期的贷款,年还款额为1000元,年实际利率为5%。在第5次还款之后调整了偿还方式。调整后,第6次偿还800元,第7次偿还(800+K)元,以后每次付款比前一次均增加K,还款期不变。求调整后的最后一次偿还额。
分别用将来法计算两种偿还方式在第5次付款之后的未偿还本金,有
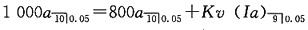
解得K=48.7914
故调整后最后一次的支付额为800+9K=1239.1
20. 两笔金额相等的30年期贷款,均以8%的利率按年分期偿还,每年末偿还一次。贷款L将等额分期偿还。贷款N每期偿还的本金金额相等,同时根据未偿还本金余额支付相应的利息。在第t年末,贷款L的偿还额首次超过贷款N,求t。
不妨假设两笔贷款均为1
对于贷款L,

对于贷款N,R
N=1/30+I
第t期对应的利息I为0.08(30-t+1)/30
故要使贷款L的支付额超过贷款N,有
R
N=1/30+0.08(30-f+1)/30≤R
L=0.0888
解得t≥10.2
故在第11年末,贷款L的支付额首次超过贷款N
21. 一笔8000元的10年期贷款按年偿还,每年末偿还一次,年利率为7%。偿还4次以后,借款人要求分4次偿还剩余的债务。新的偿还方式使贷款人在整个8年期获得了8%的年收益率。试确定调整偿还方式以后,借款人增加了多少付款。
每期偿还金额为
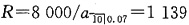
调整后,由8%的年收益率,在借款日满足
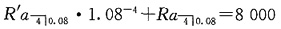
解得调整后的每期偿还金额为R'=1736.9
故通过调整,借款人增加的付款为4×1736.9-6×1139=112
22. 一笔100000元的30年期贷款,偿还方式满足下述条件:
(1)第1年末偿还X元。
(2)后来的19年,每年末的偿还金额要比上一年增加100元。在最后10年,各年的偿还额保持在前一年的水平不变。
(3)年实际利率为5%。
求X。
23. 某人从银行获得一笔贷款,期限为4年,年实际利率为8%。借款人用偿债基金方法偿还,每年末支付的总金额(包括当期的利息和向偿债基金的储蓄两部分)依次为2000元、3000元、4000元、5000元,偿债基金的年实际利率为7%。试计算贷款本金为多少?
设贷款本金为L。由已知,当期的利息为0.08L
故每年末向偿债基金的储蓄额依次为2000-0.08L,3000-0.08L,4000-0.08L,5000-0.08L
又偿债基金的年实际利率为7%,故贷款本金为:
L=(2000-0.08L)×1.073+(3000-0.08L)×1.072+(4000-0.08L)×1.07+(5000-0.08L)
解之得L=11190.11
27. 债券的面值为1000元,息票率为6%,期限为5年,到期按面值偿还。投资者所要求的收益率为8%,试计算债券在购买9个月后的价格和账面值。
价格为974.82元,账面值为930.26元(理论方法),929.82元(半理论方法),1015元(实践方法)
28. 债券的面值为1000元,期限为5年,到期按面值偿还,年息票率为6%。如果发行价格为950元,试计算该债券的收益率。
29. 债券的面值为1000元,期限为5年,到期按面值偿还,年息票收入只能按5%的利率投资,试重新计算该债券的收益率。
30. 一种面值为100的100年期债券,到期按面值偿还。已知该债券第1个10年的年息票率为10%,第2个10年的息票率为9%,第3个10年的息票率为8%,……,最后一个10年的息票率为1%。如果年收益率为5%,求该债券的购买价格。
31. 一种在年末分红的股票,当年的利润为J,利润在今后的每一年内都会以10%的速度增长,在接下来的5年内没有分红,5年后将每年利润的50%分红,如果实际收益率为21%,请计算投资者的理论购买价格。
股票未来的收益流为J(1.10)
6,它的50%将用来分红,故有
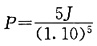
32. 一家公司利润的季度增长率为2%,每季度该公司打算拿出利润的30%作为股票的分红。在某个季度初,一个投资者购买了此公司的股票以获得10%的年收益率(每半年复利一次)。该股票的第一次分红是在该季度末,分红金额为3.00。请计算该股票的理论价格。
每个季度的实际利率为j=2.47%,股票的理论价格为P=638.3
33. 一种n年期附有8%年度息票率的债券,面值为1000。此债券在第3年末的账面值为1099.84,在第5年末的账面值为1082.27。求此债券的价格。
用BV
3,BV
4,BV
5分别代表第3,4,5年的账面值,已知Fr=1000(0.08)=80,故
1082.27=BV
5=BV
4(1+i)-80=[(BV
3)(1+i)-80](1+i)-80=1099.84(1+i)
2-80(1+i)-80
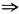
i=6.5%
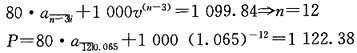
34. 已知下述债券有相同的收益率且面值均为1000:
(1)一种10年期债券,年息票率为8%,每半年支付一次息票,债券的折价为X。
(2)一种10年期债券,年息票率为9%,每半年支付一次息票,债券的溢价为Y。
(3)一种10年期债券,年息票率为10%,每半年支付一次息票,债券的溢价为2X。
请计算Y的值。
(1)
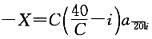
(2)
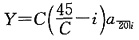
(3)
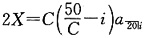
由(3)/(1)得:
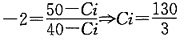
由(1)+(3)得:
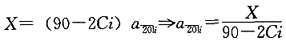
所以
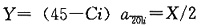
35. 一个卖空的投资者以每股10的价钱出售500股股票。一年后,每股的价钱降到7.50,此时该投资者补进500股该股票。假设交易保证金为50%,保证金的利率为5%。该股票在每季度每股分红0.1。请计算该投资者卖空的收益率。
每股的利润为10-7.50=2.50,保证金为10×0.50=5,保证金所得利息为5×0.050=0.25,分红为4×0.1=0.4,所以收益率为
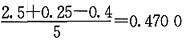
36. 某债券的面值为100元,期限为5年,年息票率为5%,2011年6月1日发行,到期按面值偿还,到期收益率为6%。请分别用精确理论方法和实践方法计算该债券在2011年12月31日的账面值。
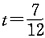
,理论方法计算的账面值为87.3509,实践方法计算的账面值为87.3526
37. 在2002年1月1日购买了一只普通股票,它将在2011年12月31日之前每年末分红15,从2012年开始,分红每年增加K%(K<6)。在年收益率为8%时的理论购买价为200.90,求K的值。
把2012年1月1日作为参考期,有t=10,则
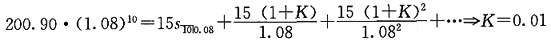
38. 一项面值为1000元的债券,年息票率为8%,每半年支付一次息票,到期偿还1100元。以价格P购买此债券将产生6%的年收益率(每半年复利一次)。偿还值的现值为190,求价格P。
39. 三种债券有同样到期偿还值和到期时间。第一种债券的年息票为40,以价格P出售;第二种债券的年息票为30,以价格Q出售;第三种债券的年息票为80。所有的价格计算都基于相同的收益率,并且所有的息票具有相同的支付频率。求第三种债券的价格。
40. 一项10年期债券的面值为1000元,年息票率为r,每年末支付一次息票,偿还值为1100。如果以价格P出售,将产生4%的年实际收益率;如果以价格(P-81.49)出售,将产生的年实际收益率;如果以价格X出售,将产生r的年实际收益率。请计算X。
41. 债券的期限为20年,面值为1000元,在每年末支付息票,到期偿还1050。如果以价格P出售可以产生8%的年实际收益率。第一次支付的息票为50,以后每次支付的息票比上一次增长3%。求价格P。
P=1050

+50[v+(1.03)v
2+(1.03)
2v
3+…+(1.03)
19v
20]=837.78
42. 投资者购买了一个面值为1000元的10年期债券,息票率为8%,每半年末支付一次息票。如果债券在到期时按面值偿还,将产生7%的名义收益率(每半年复利一次)。如果债券在第5年末被赎回,为了保证产生相同的收益率,最小的赎回值为X。求X。

 X=704.06元
X=704.06元 v14=0.25,R=144
v14=0.25,R=144 R(1-v7)=144(1-0.5)=72
R(1-v7)=144(1-0.5)=72
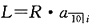
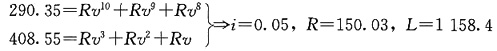
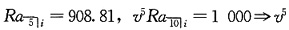 =0.661989
=0.661989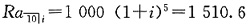
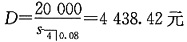
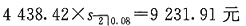
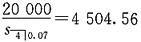 元,各年应支付的利息为20000×8%=1600。故每期总的支付金额为6104.56元
元,各年应支付的利息为20000×8%=1600。故每期总的支付金额为6104.56元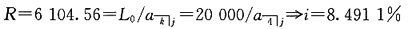

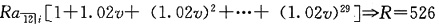
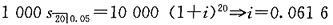
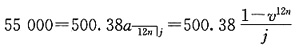
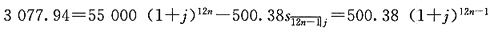
 =12,j=0.0917
=12,j=0.0917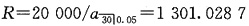
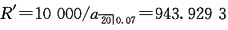 ,P'1=R'v20-1+1=243.9293
,P'1=R'v20-1+1=243.9293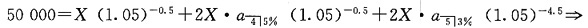 X=3278
X=3278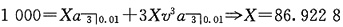
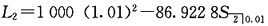 =845.3852
=845.3852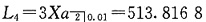
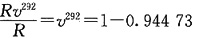
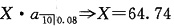
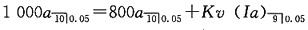

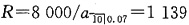
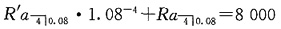
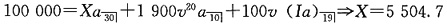
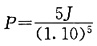
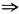 i=6.5%
i=6.5%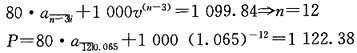
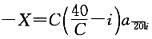
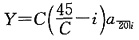
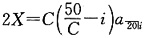
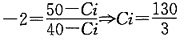
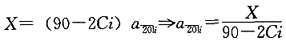
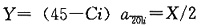
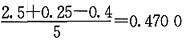
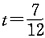 ,理论方法计算的账面值为87.3509,实践方法计算的账面值为87.3526
,理论方法计算的账面值为87.3509,实践方法计算的账面值为87.3526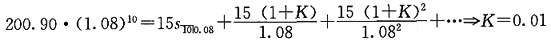
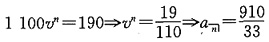
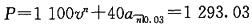
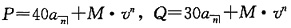 ,设第三种债券的价格为X,
,设第三种债券的价格为X, ,因此
,因此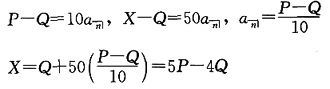

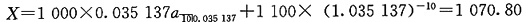
 +50[v+(1.03)v2+(1.03)2v3+…+(1.03)19v20]=837.78
+50[v+(1.03)v2+(1.03)2v3+…+(1.03)19v20]=837.78