四、综合题1. 何谓心理与教育统计学?学习它有何意义?
心理与教育统计学是专门研究如何运用统计学原理和方法,搜集、整理、分析心理与教育科学研究中获得的随机数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育活动规律的一门学科。
学习心理与教育统计学,能够依据数据的规律,揭示心理现象,找出心理与教育活动规律。
2. 选用统计方法有哪几个步骤?
首先要分析一下实验设计是否合理,即所获得的数据是否适合用统计方法去处理,正确的数量化是应用统计方法的起步,如果对数量化的过程及其意义没有了解,将一些不着边际的数据加以统计处理是毫无意义的。
其次要分析实验数据的类型,不同数据类型所使用的统计方法有很大差别,了解实验数据的类型和水平,对选用恰当的统计方法至关重要。
最后要分析数据的分布规律,如总体方差的情况,确定其是否满足所选用的统计方法的前提条件。
3. 心理与教育科学实验所获得的数据是否属于随机变量?为什么?
心理与教育科学实验所获得的数据属于随机变量。心理与教育科学研究数据具有随机性和变异性。
科学研究中因观测人员、观测工具、观测条件的变化而具有随机变化的现象。在心理和教育科学领域,研究获得的数据资料也具有一定随机性质。观测数据的这种特点,称为变异性。即便使用同一种测量工具,观测同一事物,只要是进行多次,那么获得的数据就不会完全相同。随着测量工具的完善和精确,数据的这种随机性变化就更明显。
造成数据变异的原因,出自观测过程中一些偶然的不可控制的因素,称随机因素。随机因素使测量产生的误差称作随机误差。在教育和心理科学的各类研究中,研究的对象是人的内在的种种心理现象,不仅由客观上一些偶然因素会引起测量误差,由实验者和被试主观上一些不可控制的偶然因素也会造成测量误差,也就使得心理与教育科学研究中得到的数据具有更明显的变异性。
4. 怎样理解总体、样本与个体?
总体N:据有某种特征的一类事物的全体,又称为母体、样本空间,常用N表示,其构成的基本单元为个体。特点:①大小随研究问题而变(有、无限);②总体性质由组成的个体性质而定。
样本n:从总体中抽取的一部分交个体,称为总体的一个样本。样本数目用n表示,又叫样本容量。特点:①样本容量越大,对总体的代表性越强;②样本不同,统计方法不同。
总体与样本可以相互转化。
个体:构成总体的每个基本单元称为个体。有时个体又叫做一个随机事件或样本点。
5. 统计量与参数之间有何区别和关系?
参数:总体的特性称参数,又称总体参数,是描述一个总体情况的统计指标。
统计量:样本的特征值叫做统计量,又称特征值。
二者关系:参数是一个常数,统计量随样本而变化;
参数常用希腊字母表示,统计量用英文字母表示;
当试验次数:总体大小时,二者为同一指标;
当总体无限时,二者不同,但统计量可在某种程度上作为参数的估计值。
6. 试举例说明各种数据类型之间的区别。
例如,监狱中有四个犯人,只有一张桌子,一副扑克牌,如何对他们进行区分。
第一种方法:给四个犯人命名为1、2、3、4,这里的1、2、3、4就是称名数据,因为1、2、3、4只用来区分犯人,没有其他含义,而且可以在四个犯人间互换。
第二种方法,按身高排序,即第1,第2,第3,第4,这里的1、2、3、4就是顺序数据,他们代表不同的含义,而且不能互换。
第三种方法:以桌子高度(H)为起点,用扑克牌测量犯人身高。比如四个犯人身高依次是H+20(扑克牌数量),H+40,H+25,H+50,这些数据就是等距数据。根据这些数据我们可以得出谁的身高最高,谁的最低,也可以说H+40比H+20高20张扑克牌,但不能说H+40是H+20的两倍,因为H是有数量的,这里就可以把H当作一个相对零点。
第四种方法:直接用扑克牌测量犯人身高,比如四个犯人身高依次是20(扑克牌数量),40,25,50,这里就是比率数据。根据这些数据我们可以得出谁的身高最高,谁的最低,也可以说40比20高20张扑克牌,也能说40是20的两倍。
第一种方法和第二种方法获得的数据是离散数据,计数数据,第三种方法和第四种方法获得的数据是测量数据和连续数据。
7. 下述一些数据,哪些是测量数据?哪些是计数数据?其数值意味着什么?
0千克(重量);89.85厘米(长度);199.2秒(时间);93.5分(分数)是测量数据。
17人(人数);25本(书本数)是计数数据。
8. 说明下面符号代表的意义。
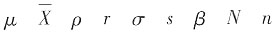
μ反映总体集中情况的统计指标,即总体平均数或期望值。
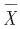
反映样本平均数。
ρ表示某一事物两个特性总体之间关系的统计指标,相关系数。
r样本相关系数。
σ反映总体分散情况的统计指标标准差。
s样本标准差。
β表示两个特性中体之间数量关系的回归系数。
N有限个体数目的总体。
n样本容量,样本大小。
9. 结合所学心理学知识,谈谈你对心理统计思想的初步理解。
掌握统计思想更重要,心理统计不仅仅是记公式,做计算,一定要掌握心理统计的基本原理,需要满足的条件,比如数据类型,总体分布等。
10. 统计分组应注意哪些问题?
进行统计分组时需要注意下列问题:(1)分组要以被研究对象的本质特性为基础面对大量原始数据进行分组时,有时需要先做初步的分类,分类或分组一定是要选择与被研究现象的本质的关的特性为依据,才能确保分类或分组的正确。在心理与教育学研究方面,专业知识的了解和熟悉对分组的正确进行有重要的作用。例如在学业成绩研究中按学科性质分类,在整理智力测验结果时,按言语智力、操作智力和总的智力分数分类等。(2)分类标志要明确,要能包括所有的数据对数据进行分组时,所依据的特性称为分组或分类的标志。整理数据时,分组标志要明确并在整理数据的过程中前后一致。这就是说,关于被研究现象本质特性的概念要明确,不能既是这个又是那个。另外,所依据的标志必须能将全部数据包括进去,不能有遗漏,也不能中途改变。
11. 直条图适合哪种资料?自选数据绘制直条图。
直条图或叫条形图:主要用于表示离散型数据资料,即计数资料。
12. 圆形图适合哪种资料?自选数据绘制圆形图。
圆形图或叫饼图:主要用于描述间断性资料,目的是为显示多部分在整体中所占的比重大小,以及各部分之间的比较。
13. 将下面的反应时测定资料编制成次数分布表、累加次数分布表、直方图、次数多边形图。
177.5 167.4 116.7 130.9 199.1 198.3 225.0 212.0 180.0 171.0 144.0
138.0 191.0 171.5 147.0 172.0 195.5 190.0 206.7 153.2 217.0 179.2
242.2 212.8 171.0 241.0 176.1 165.4 201.0 145.5 163.0 178.0 162.0
188.1 176.5 172.2 215.0 177.9 180.5 193.0 190.5 167.3 170.5 189.5
180.1 217.0 186.3 180.0 182.5 171.0 147.0 160.5 153.2 157.5 143.5
148.5 146.4 150.5 177.1 200.1 137.5 143.7 179.5 185.5 181.6
(1)求全距
R=Xmax-Xmin=242.2-116.7=125.5
(2)确定组数和组距
N=65代入公式K=1.87(N-1)2/5,得K=9.8,理论组数为10,组距为12.5,由于理论分组不能包括116.7,因此组数定为11,组距为12.5
(3)列分组区间,登记与计算次数
(4)编制次数分布表
(5)编制累积次数分布表
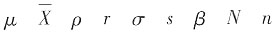
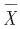 反映样本平均数。
反映样本平均数。