一、单项选择题1. 两个圆C
1:x
2+y
2+2x+2y-2=0与C
2:x
2+y
2-4x-2y+1=0的公切线有且仅有______.
A B C D
B
[解析] 两圆的圆心分别是(-1,-1),(2,1),半径分别是2,2,两圆圆心距离:
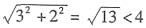
,说明两圆相交.因而公切线只有两条,故选B.
2. 复数
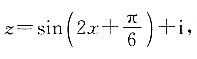
且
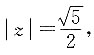
z对应的点在第一象限,则x的取值范围为______.
A.

B.
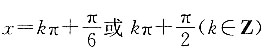
C.
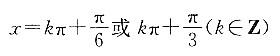
D.
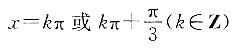
A B C D
D
[解析] 因为
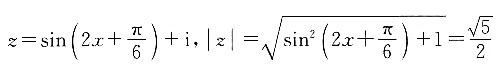
,所以
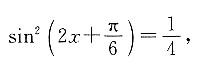
又因为z对应的点在第一象限,所以

,解得x=kπ或

7. 已知抛物线y
2=2px(p>0),过其焦点且斜率为1的直线交抛物线于A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的标准方程为______.
A B C D
B
[解析] 设A(x
1,y
1)、B(x
2,y
2),则有
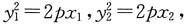
两式相减得:(y
1-y
2)(y
1+y
2)=2p(x
1-x
2),又因为直线的斜率为1,所以
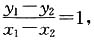
所以有y
1+y
2=2p,又线段AB的中点的纵坐标为2,即y
1+y
2=4,所以p=2,所以抛物线的准线方程为
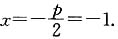
故选B.
9. 设D、E、F分别是△ABC的三边BC、CA、AB上的点,且
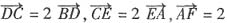
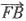
,则
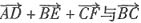
______.
- A.反向平行
- B.同向平行
- C.互相垂直
- D.既不平行也不垂直
A B C D
A
[解析] 由定比分点的向量式得:
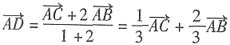
,同理得
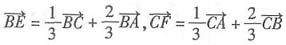
,以上三式相加得
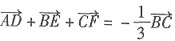
,所以选A.
二、填空题1. ______是数学科学理论的基本特点.
严谨性
[解析] 严谨性是数学科学理论的基本特点.它要求数学结论的表述必须精炼、准确.而对结论的推理论证,要求步步有根据,处处符合逻辑理论的要求.
2. 在△ABC中,sin
2A<sin
2B+sin
2C-sinBsinC,则A的取值范围是______.
0<A≤
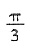
[解析] 由sin
2A≤sin
2B+sin
2c-sinBsinC得a
2≤b
2+C
2-bc,即
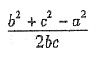
≥
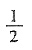
,∴
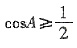
,∴0<A<π,故0<A≤
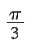
.
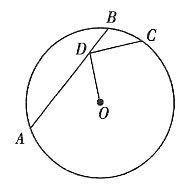
3. 如图,点D在⊙O的弦AB上移动,AB=4,连接OD,过点D作OD的垂线交⊙O于点C,则CD的最大值为______.
2
[解析] 因为
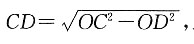
且OC为⊙O的半径,是定值,所以当OD取最小值时,CD取最大值.显然当OD⊥AB时,OD取最小值,且此时
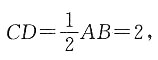
即为所求的最大值.
4. 设P:关于x的不等式2
|x|<a的解集为
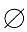
,Q:函数y=lg(ax
2-x+a)的定义域为R.如果P和Q有且仅有一个正确,则a的取值范围是______.
[解析] P:∵2
|x|≥1,且不等式2
|x|<α的解集为
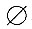
,∴a≤1.
Q:ax
2-x+a>0恒成立.
①若a=0,则-x>0(不符合题意,舍去);②若a≠0,则
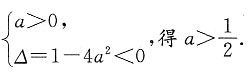
∵P和Q有且仅有一个正确,∴P真Q假或者P假Q真.
若P真Q假,则
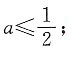
若P假Q真,则a>1.
综上所述,所求a的取值范围是
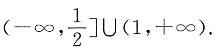
5. 计算:
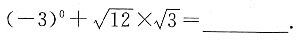
7
[解析]
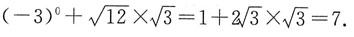
三、计算题1. 已知函数
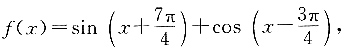
x∈R.求f(x)的最小正周期和最小值.
解:f(x)=sin xcos
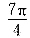
+cos xsin
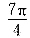
+cos xcos

+sin xsin

=
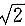
sin x-
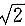
cos x=2sin(x-
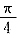
),
所以f(x)的最小正周期T=2π,最小值f(x)
min=-2.
2. 求这三条曲线的方程;
解:设抛物线方程为yc
=2px(p>0),将M(1,2)代入方程得P=2,
∴抛物线方程为:y
2=4x.
由题意知椭圆、双曲线的焦点为F
1(-1,0),F
2(1,0),∴c=1.
对于椭圆,
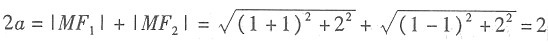
+
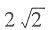
.
∴椭圆方程为:
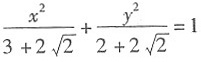
.
对于双曲线,
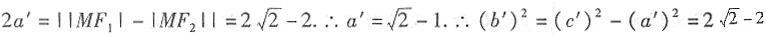
.
∴双曲线方程为:
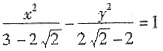
.
3. 已知动直线l过点P(3,0),交抛物线于A,B两点,是否存在垂直于x轴的直线l',被以AP为直径的圆截得的弦长为定值?若存在,求出l'的方程;若不存在,说明理由.
解:设AP的中点为C,l'的方程为:x=a,以AP为直径的圆交l'于D,E两点,DE中点为H.
令
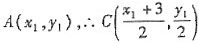
.
∴

,

,
∴
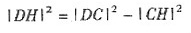
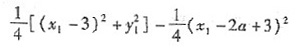
=
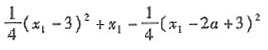
=
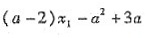
.
当a=2时,|DH|
2=-4+6=2为定值,
即弦长DE为定值,此时l'的方程为x=2.
∴存在直线l':x=2满足条件.
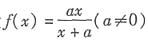 ,令a1=1,an+1=f(an),又bn=an·an+1,n∈N+.
,令a1=1,an+1=f(an),又bn=an·an+1,n∈N+.4. 判断数列
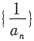
是等差数列还是等比数列,并求数列{a
n}的通项公式;
解:因为
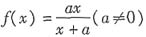
,所以
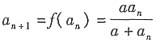
,
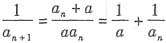
,故数列
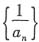
是等差数列.公差
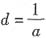
,
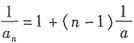
,所以
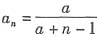
.
5. 求数列{b
n}的前n项和.
解:
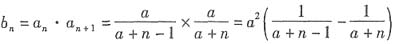
数列{b
n}的前n项和
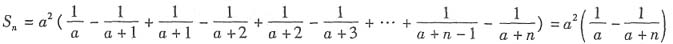
.
6. 设△ABC的内角A、B、C的对边长分别为a、b、c,
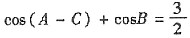
,b
2=ac,求∠B.
解:由
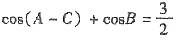
及B=π-(A+C)得cos(A-C)-cos(A+C)=
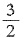
,即cosAcosC+sinAsinC-(cosAcosC-sinAsinC)=
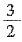
,sinAsinC=

.
又由b
2=ac及正弦定理得sin
2B=sinAsinC,
故
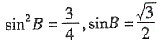
或
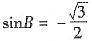
(舍去).
于是
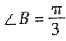
或
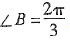
,又由b
2=ac知b≤a或b≤c,
所以
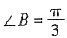
.
7. 求实数a的取值范围;
解:令g(x)=f(x)-x=x
2+(a-1)x+a,
则由0<x
1<x
2<1得,
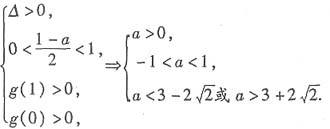
∴
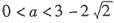
,∴实数a的取值范围是
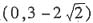
.
8. 试比较f(0)f(1)-f(0)与
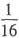
的大小,并说明理由.
解:f(0)f(1)-f(0)=2a
2,
设h(a)=2a
2,∵当a>0时,h(a)单调递增,
∴
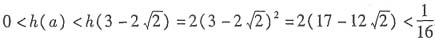
.
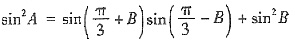 .
.10. 若
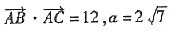
,求b、c(其中b<c).
解:由
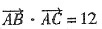
可得cbcosA=12 ①,由(1)知
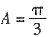
,所以cb=24 ②,
由余弦定理知a
2=c
2+b
2-2cbcosA,将
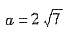
及①代入,得c
2+b
2=52 ③,③+②×2,
得(c+b)
2=100,所以c+b=10.因此,c,b是一元二次方程t
2-10t+24=0的两个根.
解此方程并由c>b知c=6,b=4.
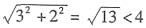 ,说明两圆相交.因而公切线只有两条,故选B.
,说明两圆相交.因而公切线只有两条,故选B.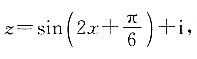 且
且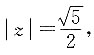 z对应的点在第一象限,则x的取值范围为______.
z对应的点在第一象限,则x的取值范围为______.
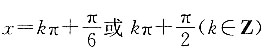
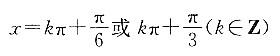
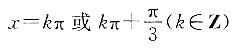
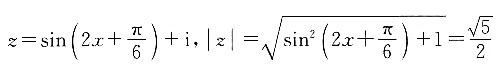 ,所以
,所以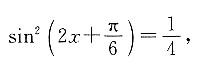 又因为z对应的点在第一象限,所以
又因为z对应的点在第一象限,所以 ,解得x=kπ或
,解得x=kπ或
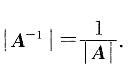 因此
因此
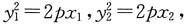 两式相减得:(y1-y2)(y1+y2)=2p(x1-x2),又因为直线的斜率为1,所以
两式相减得:(y1-y2)(y1+y2)=2p(x1-x2),又因为直线的斜率为1,所以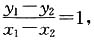 所以有y1+y2=2p,又线段AB的中点的纵坐标为2,即y1+y2=4,所以p=2,所以抛物线的准线方程为
所以有y1+y2=2p,又线段AB的中点的纵坐标为2,即y1+y2=4,所以p=2,所以抛物线的准线方程为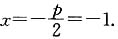 故选B.
故选B.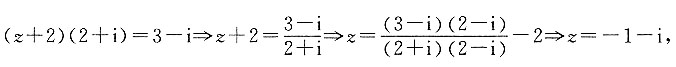 因此本题选C.
因此本题选C.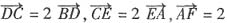
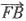 ,则
,则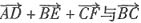 ______.
______.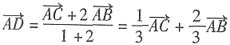 ,同理得
,同理得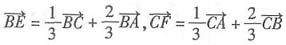 ,以上三式相加得
,以上三式相加得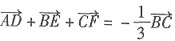 ,所以选A.
,所以选A.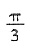
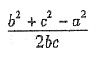 ≥
≥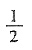 ,∴
,∴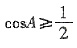 ,∴0<A<π,故0<A≤
,∴0<A<π,故0<A≤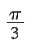 .
.
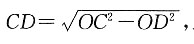 且OC为⊙O的半径,是定值,所以当OD取最小值时,CD取最大值.显然当OD⊥AB时,OD取最小值,且此时
且OC为⊙O的半径,是定值,所以当OD取最小值时,CD取最大值.显然当OD⊥AB时,OD取最小值,且此时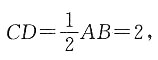 即为所求的最大值.
即为所求的最大值. ,Q:函数y=lg(ax2-x+a)的定义域为R.如果P和Q有且仅有一个正确,则a的取值范围是______.
,Q:函数y=lg(ax2-x+a)的定义域为R.如果P和Q有且仅有一个正确,则a的取值范围是______.
 ,∴a≤1.
,∴a≤1.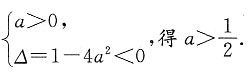
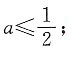 若P假Q真,则a>1.
若P假Q真,则a>1.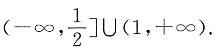
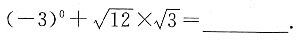
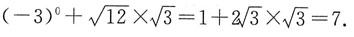
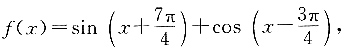 x∈R.求f(x)的最小正周期和最小值.
x∈R.求f(x)的最小正周期和最小值.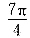 +cos xsin
+cos xsin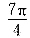 +cos xcos
+cos xcos +sin xsin
+sin xsin =
=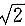 sin x-
sin x-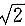 cos x=2sin(x-
cos x=2sin(x-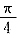 ),
),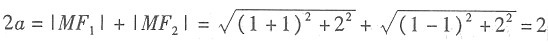 +
+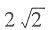 .
.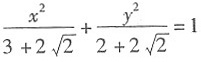 .
.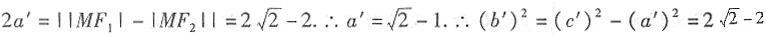 .
.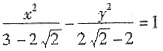 .
.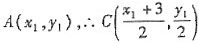 .
. ,
, ,
,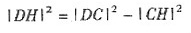
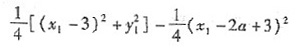
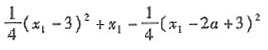
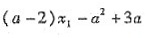 .
.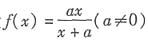 ,令a1=1,an+1=f(an),又bn=an·an+1,n∈N+.
,令a1=1,an+1=f(an),又bn=an·an+1,n∈N+.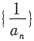 是等差数列还是等比数列,并求数列{an}的通项公式;
是等差数列还是等比数列,并求数列{an}的通项公式;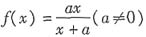 ,所以
,所以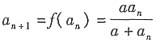 ,
,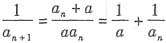 ,故数列
,故数列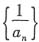 是等差数列.公差
是等差数列.公差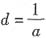 ,
,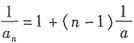 ,所以
,所以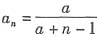 .
.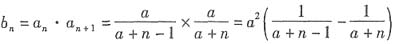
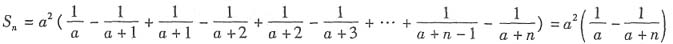 .
.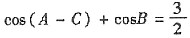 ,b2=ac,求∠B.
,b2=ac,求∠B.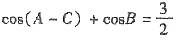 及B=π-(A+C)得cos(A-C)-cos(A+C)=
及B=π-(A+C)得cos(A-C)-cos(A+C)=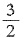 ,即cosAcosC+sinAsinC-(cosAcosC-sinAsinC)=
,即cosAcosC+sinAsinC-(cosAcosC-sinAsinC)=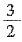 ,sinAsinC=
,sinAsinC= .
.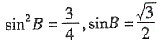 或
或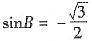 (舍去).
(舍去).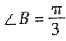 或
或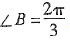 ,又由b2=ac知b≤a或b≤c,
,又由b2=ac知b≤a或b≤c,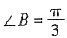 .
.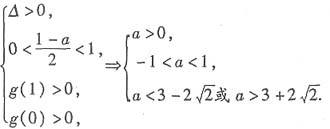
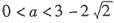 ,∴实数a的取值范围是
,∴实数a的取值范围是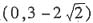 .
.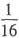 的大小,并说明理由.
的大小,并说明理由.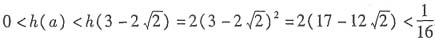 .
.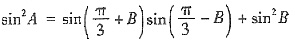 .
.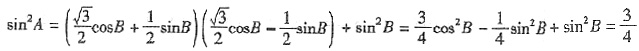 ,所以
,所以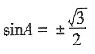 .又A为锐角,所以
.又A为锐角,所以 .
.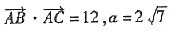 ,求b、c(其中b<c).
,求b、c(其中b<c).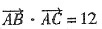 可得cbcosA=12 ①,由(1)知
可得cbcosA=12 ①,由(1)知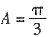 ,所以cb=24 ②,
,所以cb=24 ②,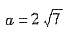 及①代入,得c2+b2=52 ③,③+②×2,
及①代入,得c2+b2=52 ③,③+②×2,