一、单项选择题5. 给出下列三个命题:
①函数
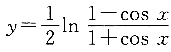
与
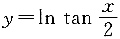
是同一函数;
②若函数y=f(x)与y=g(x)的图象关于直线y=x对称,则函数y=f(x)与y=
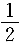
g(x)的图象也关于直线y=x对称;
③若奇函数f(x)对定义域内任意x都有f(x)=f(2-x),则f(x)为周期函数.其中真命题是______.
A B C D
C
[解析] ①函数
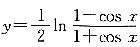
的定义域满足

即cos x≠±1,x≠kπ(k∈Z),y=ln tan
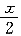
的定义域满足
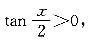
即
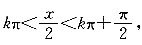
2kπ<x<2kπ+π(k∈Z),两函数定义域不相同,不是同一函数;②函数y=f(2x)反解得2x=f
-1(y),即
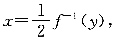
所以y=f(2x)的反函数为
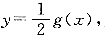
所以②正确;③因为f(x)是奇函数,则f(-z)=-f(x),又f(x)=f(2-x),所以-f(-x)=f(2-x),即f(x+2)=-f(z),所以f(x+4)=-f(x+2),f(x)=f(x+4),所以f(x)的周期为4,故选C.
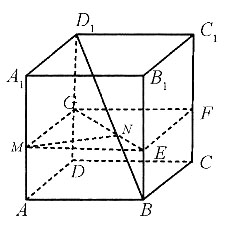
6. 如图所示,BD
1为正方体的体对角线,长度为
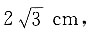
M、N分别为线段AA
1、BD
1上的动点.t=0s时,M与点A重合,N与点B重合;经过5s后,M与点A
1重合,N与点D
1重合.则下列图象能表示MN长度s与时间t的关系的是______.
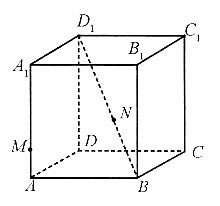
A.
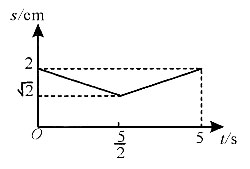
B.
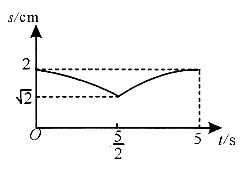
C.
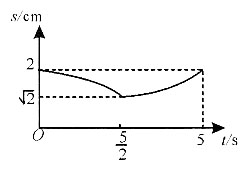
D.
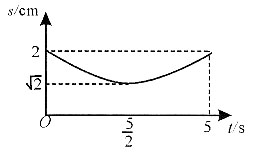
A B C D
D
[解析] 根据B
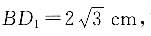
可知
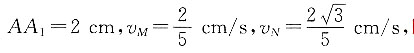
N点到底面的距离等于M点到底面的距离,即MN一直在平行于底面的平面内,如图,过M点作面MEFG//底面ABCD,N点运动的轨迹的投影在EG上,即EG与BD
1的交点为N,连接MN,
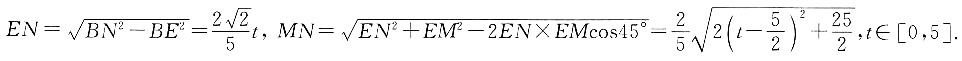
在

时,取最小值
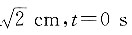
或5s时取最大值2cm,且
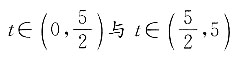
时的图象关于
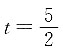
对称,排除C项;s与t非线性关系,排除A项;求MN的导数可得
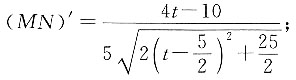
所以答案选D.
7. 如果AB=BA,矩阵B就称为A的可交换矩阵.设矩阵
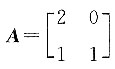
,则下列矩阵中与A可交换的矩阵B为______.
A.
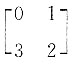
B.
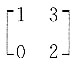
C.
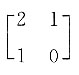
D.
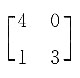
A B C D
D
[解析] 将A项中的矩阵代入,
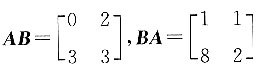
,AB≠BA.将B项中的矩阵代入,
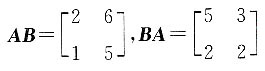
,AB≠BA.将C项中的矩阵代入,
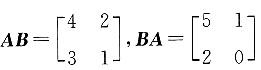
,AB≠BA.将D项中的矩阵代入,
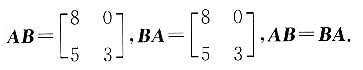
二、填空题1. 已知行列式
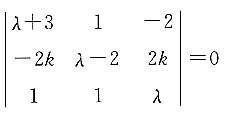
,则λ=______.
-1或±2
[解析] 将行列式第3列加至第1列,再把第1行的-1倍加至第3行,然后按第3行展开如下:
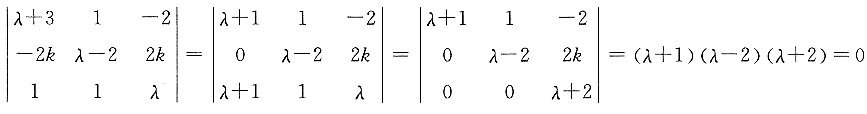
,所以λ=-1或λ=±2.
2. 已知集合M={x|-1≤x≤3},N={x|1<x<6,x∈Z},则M∩N=______.
{2,3}
[解析] 由题干可知,集合N={2,3,4,5},则M∩N={2,3}.
3. 已知奇函数y=f(x)的图象关于
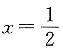
对称且周期为2,则f(1)+f(2)+…+f(9)+f(10)=______.
0
[解析] 因为y=f(x)为奇函数,则f(1)=-f(-1),f(x)是周期为2的周期函数,则f(x)=f(x+2),当x=-1时,f(-1)=f(1),所以f(-1)=-f(-1),即f(1)=f(-1)=0.已知函数关于
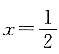
对称,则f(0)=f(1)=0,f(0)=f(2)=f(4)=f(6)=f(8)=f(10)=0,f(1)=f(3)=f(5)=f(7)=f(9)=0.所以原式=0.
4. 一纳米等于十亿分之一米,则60米=______纳米.(用科学计数法表示)
6×1010
[解析]本题主要考查科学计数法.
已知1nm=10-9m,则60m=60×109nm=6×1010nm.
5. 已知函数f(x)=|x
2-ax-b|( x∈R,b≠0),给出以下三个条件:
(1)存在x
0∈R,使得f(-x
0)≠f(x
0);
(2)f(3)=f(0)成立;
(3)f(x)在区间[-a,+∞]上是增函数.
若f(x)同时满足条件______和______(填入两个条件的编号),则f(x)的一个可能的解析式为f(x)=______.
(1)(2) |x2-3x+1|(或(1)(3) x2+2(x+1),或(2)(3) |x2+3x-9|)
[解析] 满足条件(1)(2)时,f(x)=|x2-3x+1|等;满足(1)(3)时,f(x)=|x2+2x+1|等;满足条件(2)(3)时,f(x)=|x2+3x-9|等.
三、计算题1. 已知e是自然对数的底数,计算不定积分
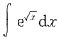
.
解:令t=
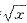
(t>0),则原不定积分可化为:
∫e'dt
2=2∫te'dt=2∫tde'=2(te'-∫e'dt)=2(te'-e')=2(t-1)e',
故原式=
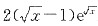
.
2. △ABC的内角A、B、C的对边分别为a、b、c.已知A-C=90°,
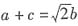
,求C.
解:由A-C=90°得A=90°+C,B=180°-(A+C)=90°-2C.由
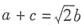
及正弦定理得
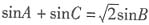
,而sinA=sin(90°+C)=cosC,sinB=sin(90°-2C)=cos2C故有
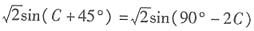
,又因为0°<C<90°,故有C+45°=90°-2C,得3C=45°,即C=15°.
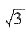 ,∠ABC=60°.
,∠ABC=60°.
3. 证明:AB⊥A
1C;
证明:∵三棱柱ABC-A
1B
1C
1为直三棱柱,∴AB⊥AA
1.在△ABC中,AB=1,AC=
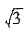
,∠ABC=60°,由正弦定理得∠ACB=30°,∴∠BAC=90°,即AB⊥AC.∴AB⊥平面ACC
1A
1,又A
1C
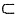
平面ACC
1A
1,∴AB⊥A
1C.
4. 求二面角A-A
1C-B.
证明:作AD⊥A
1C交A
1C于D点,连结BD,由三垂线定理知BD⊥A
1C,∴∠ADB为二面角A-A
1C-B的平面角.
在Rt△AA
1C中,
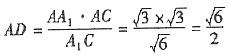
,在Rt△BAD中,
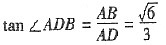
,∴∠ADB=arctan
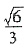
,即二面角A-A
1C-B的大小为arctan
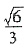
.
5. 解方程组:
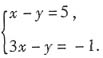
解:
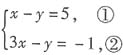
②-①,得3x-x=-6,x=-3,代入①中,得-3-y=5,y=-8.所以原方程组的解为
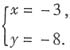
6. 已知等差数列{a
n}满足a
2=0,a
6+a
8=-10,求数列{a
n}的通项公式.
解:设等差数列{a
n}的公差为d,由已知条件可得
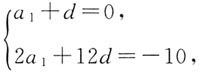
解得
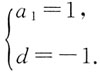
故数列{a
n}的通项公式为a
n=2-n.
7. 如图,直线y=kx将抛物线y=2x-x
2与x轴所围成的图形分为面积相等的两个部分,求k的值.
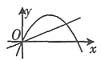
解:抛物线y=2x-x
2与z轴两交点的横坐标为x
1=0,x
2=2,所以抛物线与x轴所围图形的面积
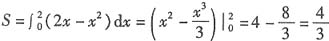
.
抛物线y=2x-x
2与y=kx两交点的横坐标为x'
1=0,x'
2=2-k,
所以
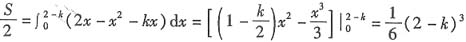
,又知
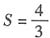
,所以(2-k)
3=4,则
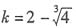
.
8. 求极限
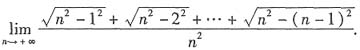
.
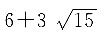
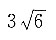
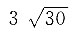
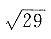
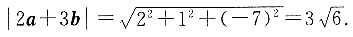
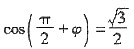 ,且
,且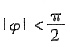 ,则
,则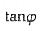 =______.
=______.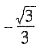
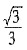
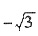
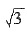
 得
得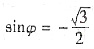 ,又
,又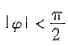 ,∴
,∴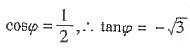 ,
,
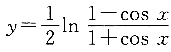 与
与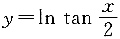 是同一函数;
是同一函数;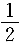 g(x)的图象也关于直线y=x对称;
g(x)的图象也关于直线y=x对称;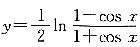 的定义域满足
的定义域满足 即cos x≠±1,x≠kπ(k∈Z),y=ln tan
即cos x≠±1,x≠kπ(k∈Z),y=ln tan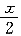 的定义域满足
的定义域满足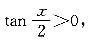 即
即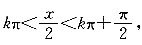 2kπ<x<2kπ+π(k∈Z),两函数定义域不相同,不是同一函数;②函数y=f(2x)反解得2x=f-1(y),即
2kπ<x<2kπ+π(k∈Z),两函数定义域不相同,不是同一函数;②函数y=f(2x)反解得2x=f-1(y),即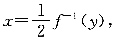 所以y=f(2x)的反函数为
所以y=f(2x)的反函数为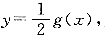 所以②正确;③因为f(x)是奇函数,则f(-z)=-f(x),又f(x)=f(2-x),所以-f(-x)=f(2-x),即f(x+2)=-f(z),所以f(x+4)=-f(x+2),f(x)=f(x+4),所以f(x)的周期为4,故选C.
所以②正确;③因为f(x)是奇函数,则f(-z)=-f(x),又f(x)=f(2-x),所以-f(-x)=f(2-x),即f(x+2)=-f(z),所以f(x+4)=-f(x+2),f(x)=f(x+4),所以f(x)的周期为4,故选C.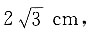 M、N分别为线段AA1、BD1上的动点.t=0s时,M与点A重合,N与点B重合;经过5s后,M与点A1重合,N与点D1重合.则下列图象能表示MN长度s与时间t的关系的是______.
M、N分别为线段AA1、BD1上的动点.t=0s时,M与点A重合,N与点B重合;经过5s后,M与点A1重合,N与点D1重合.则下列图象能表示MN长度s与时间t的关系的是______.




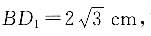 可知
可知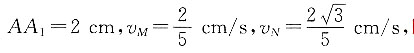 N点到底面的距离等于M点到底面的距离,即MN一直在平行于底面的平面内,如图,过M点作面MEFG//底面ABCD,N点运动的轨迹的投影在EG上,即EG与BD1的交点为N,连接MN,
N点到底面的距离等于M点到底面的距离,即MN一直在平行于底面的平面内,如图,过M点作面MEFG//底面ABCD,N点运动的轨迹的投影在EG上,即EG与BD1的交点为N,连接MN,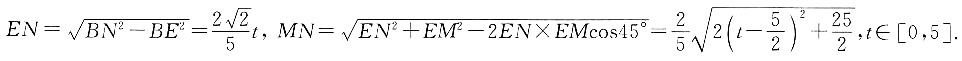 在
在 时,取最小值
时,取最小值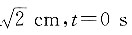 或5s时取最大值2cm,且
或5s时取最大值2cm,且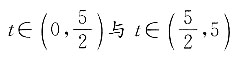 时的图象关于
时的图象关于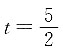 对称,排除C项;s与t非线性关系,排除A项;求MN的导数可得
对称,排除C项;s与t非线性关系,排除A项;求MN的导数可得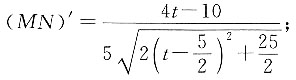 所以答案选D.
所以答案选D.
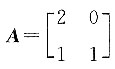 ,则下列矩阵中与A可交换的矩阵B为______.
,则下列矩阵中与A可交换的矩阵B为______.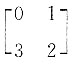

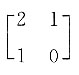
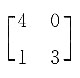
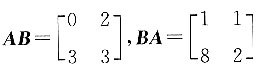 ,AB≠BA.将B项中的矩阵代入,
,AB≠BA.将B项中的矩阵代入,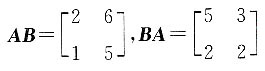 ,AB≠BA.将C项中的矩阵代入,
,AB≠BA.将C项中的矩阵代入,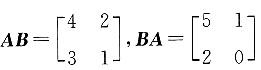 ,AB≠BA.将D项中的矩阵代入,
,AB≠BA.将D项中的矩阵代入,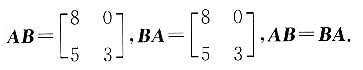
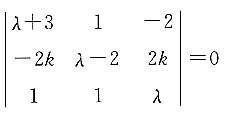 ,则λ=______.
,则λ=______.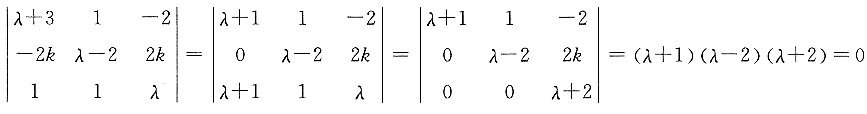 ,所以λ=-1或λ=±2.
,所以λ=-1或λ=±2.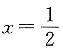 对称且周期为2,则f(1)+f(2)+…+f(9)+f(10)=______.
对称且周期为2,则f(1)+f(2)+…+f(9)+f(10)=______.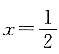 对称,则f(0)=f(1)=0,f(0)=f(2)=f(4)=f(6)=f(8)=f(10)=0,f(1)=f(3)=f(5)=f(7)=f(9)=0.所以原式=0.
对称,则f(0)=f(1)=0,f(0)=f(2)=f(4)=f(6)=f(8)=f(10)=0,f(1)=f(3)=f(5)=f(7)=f(9)=0.所以原式=0.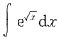 .
.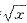 (t>0),则原不定积分可化为:
(t>0),则原不定积分可化为: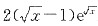 .
.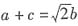 ,求C.
,求C.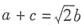 及正弦定理得
及正弦定理得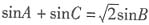 ,而sinA=sin(90°+C)=cosC,sinB=sin(90°-2C)=cos2C故有
,而sinA=sin(90°+C)=cosC,sinB=sin(90°-2C)=cos2C故有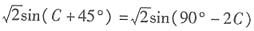 ,又因为0°<C<90°,故有C+45°=90°-2C,得3C=45°,即C=15°.
,又因为0°<C<90°,故有C+45°=90°-2C,得3C=45°,即C=15°.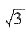 ,∠ABC=60°.
,∠ABC=60°.
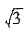 ,∠ABC=60°,由正弦定理得∠ACB=30°,∴∠BAC=90°,即AB⊥AC.∴AB⊥平面ACC1A1,又A1C
,∠ABC=60°,由正弦定理得∠ACB=30°,∴∠BAC=90°,即AB⊥AC.∴AB⊥平面ACC1A1,又A1C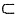 平面ACC1A1,∴AB⊥A1C.
平面ACC1A1,∴AB⊥A1C.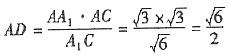 ,在Rt△BAD中,
,在Rt△BAD中,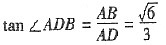 ,∴∠ADB=arctan
,∴∠ADB=arctan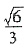 ,即二面角A-A1C-B的大小为arctan
,即二面角A-A1C-B的大小为arctan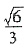 .
.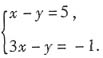
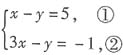 ②-①,得3x-x=-6,x=-3,代入①中,得-3-y=5,y=-8.所以原方程组的解为
②-①,得3x-x=-6,x=-3,代入①中,得-3-y=5,y=-8.所以原方程组的解为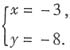
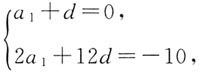 解得
解得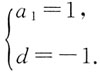 故数列{an}的通项公式为an=2-n.
故数列{an}的通项公式为an=2-n.
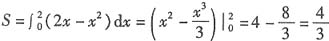 .
.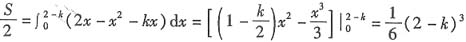 ,又知
,又知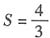 ,所以(2-k)3=4,则
,所以(2-k)3=4,则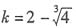 .
.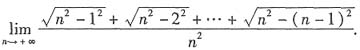 .
.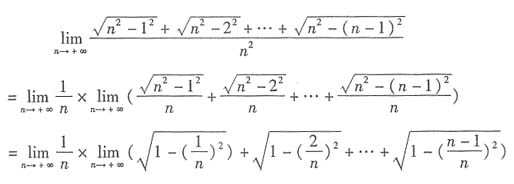
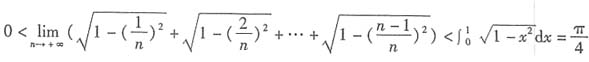 .
.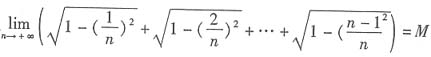 ,M为一定值.
,M为一定值.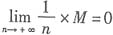 .
.