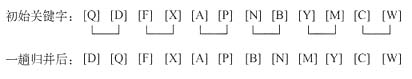一、单项选择题11. 若一棵二叉树的前序遍历序列为aebdc,后序遍历序列为bcdea,则根结点的孩子结点______
A B C D
A
[考点] 二叉树
[解析] 二叉树是每个结点最多有两个子树的树结构,通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。所谓遍历(traversal),是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。而通常情况下,如果中序遍历未知,则无法还原出二叉树。但本题只要求判断根结点的孩子结点,因此,是可以实现的。
二叉树中的前序遍历也叫作先根遍历、先序遍历,遵循的原则为“根左右”,即首先遍历根结点,再遍历根结点的左子树结点,最后遍历根结点的右子树结点。从前序遍历序列可知,结点e紧跟着结点a,可得结论:①结点a为根结点;②当结点e为结点a的右孩子时,结点a有且仅有结点e-个孩子。
二叉树中的后序遍历也叫作后根遍历,遵循的原则为“左右根”,即首先遍历左子树结点,再遍历右子树结点,最后遍历根结点。从后序遍历序列可知,结点e之后紧跟结点a,可得结论:当结点e为结点a的左孩子时,结点a有且仅有结点e一个孩子。从前面3个结论可知根结点的孩子有且仅有e。
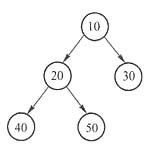
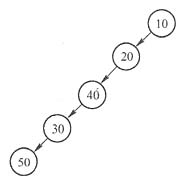
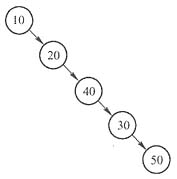
通过前序遍历序列和后序遍历序列不能确定唯一的一棵二叉树,本例存在如下图所示的两种情况。
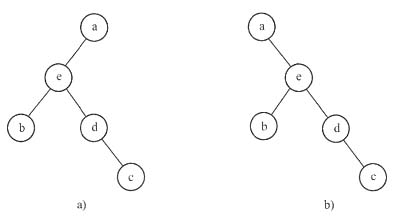 二叉树的两种情况
二叉树的两种情况 无论是以上哪一种情况,都可以看出根结点的孩子结点只有e。通过以上分析可知,选项
A是正确的。
20. 无向图G=(V,E),其中V={a,b,c,d,e,f},E={<a,b>,<a,e>,<a,c>,<b,e>,<e,f>,<f,d>,<e,d>},对该图进行深度优先排序,得到的顶点序列正确的是______
- A.a,b,e,c,d,f
- B.a,C,f,e,b,d
- C.a,e,b,c,f,d
- D.a,e,d,f,c,b
A B C D
D
[考点] 图
[解析] 本题要选出正确答案,必须弄明白无向图的深度优先遍历的原理。其实,图的深度优先遍历类似于树的前序遍历。假设给定无向图G的初态是所有顶点均未曾被访问过,深度优先遍历过程是这样的:在无向图G中任选一个顶点v为初始出发点(源点),首先访问源点v,并将其标记为已访问过,然后,依次从源点v出发,搜索源点v的每个相邻结点w。如果结点w未曾被访问过,那么以结点w为新的出发点继续进行深度优先遍历,直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。如果此时图中仍有未访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。
图的深度优先遍历伪代码如下所示。
(1)访问顶点v; visited[v]=1; //算法执行前visited[n]=0
(2)w=顶点v的第一个邻接点;
(3)while(w存在)
if(w未被访问)
从顶点w出发递归执行该算法;
w=顶点v的下一个邻接点;
本题中,按照上述方法可知,选项D正确。
28. 某段文本中各个字母出现的频率分别是{a:4, b:3, 0:12, h:7, i:10},若使用哈夫曼编码,则可能的编码是______
- A.a(000)b(001)h(01)i(10)o(11)
- B.a(0000)b(0001)h(001)o(01)i(1)
- C.a(000)b(001)h(01)i(10)o(00)
- D.a(0000)b(0001)h(001)o(000)i(1)
A B C D
A
[解析] 哈夫曼编码(Huffman Coding)使用到一种叫作“前缀编码”的技术,即任意一个数据的编码都不是另一个数据编码的前缀。而最优二叉树即哈夫曼树(带权路径长度最小的二叉树)就是一种实现哈夫曼编码的方式。哈夫曼编码的过程就是构造哈夫曼树的过程,构造哈夫曼树的相应算法如下图所示。
 构造哈夫曼树1
构造哈夫曼树1 (1)有一组需要编码且带有权值的字母,例如a(4)、b(8)、c(1)、d(2)、e(11)。括号内分别为各字母相对应的权值。
(2)选取字母中权值较小的c(1)、d(2)组成一个新二叉树,其父结点的权值为这两个字母权值之和,记为f(3),然后将该结点加入到原字母序列中去(不包括已经选择的权值最小的两个字母),则剩下的字母为a(4)、b(8)、e(11)和f(3)。
(3)重复进行步骤(2),直到所有字母都加入二叉树中为止,最后得到的二叉树如下图所示。
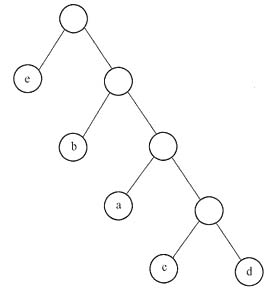 构造哈夫曼树2
构造哈夫曼树2 如果用0表示左分支,1表示右分支,则得到的编码为:a(110)、b(10)、c(1110)、d(1111)、e(0)。
由于哈夫曼编码不是唯一的,本题主要的思路为:对于每个选项而言,首先画出二叉树结构图,然后判断其是否满足哈夫曼编码的条件。
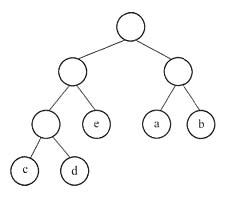
选项A对应的二叉树结构如下图所示。显然,满足哈夫曼编码的条件。
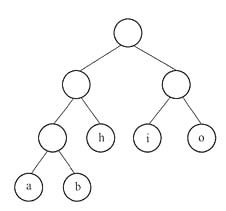 选项A对应的二叉树
选项A对应的二叉树 选项B对应的二叉树结构如下图所示。对于这个二叉树而言,第一步选出权值小的两个结点a:4和b:3,其父结点的权值为f1:7,然后从列表里删除结点a和结点b,增加结点f1,结果为{o:12, h:7, i:10, f1:7};接着再次选出权值较小的两个结点h和f1,构造它们的父结点f2:14,然后从列表里删除结点h与f1,增加新结点f2:{o:12, i:10, f2:14};接下来应该选权值较小的两个结点o与i。所以,结点o与i肯定是兄弟结点,这个二叉树不满足条件。因此,选项B错误。
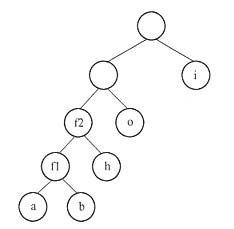 选项B对应的二叉树
选项B对应的二叉树 同理,对于选项C和选项D可以采用同样的方法进行分析。所以,本题的答案为A。
二、多项选择题4. 2-3树是一种特殊的树,它满足以下两个条件:
(1)每个内部结点有2个或3个子结点。
(2)所有的叶子结点到根的路径长度相同。
如果一棵2-3树有9个叶子结点,则它可能有的非叶子结点个数为______
A B C D
AC
[考点] 二叉树
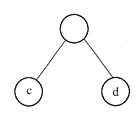
[解析] 根据条件(2),叶子结点只能在同一层,根据条件(1),上一层的父结点只能是3个或4个,只能是下图所示的两种结果。
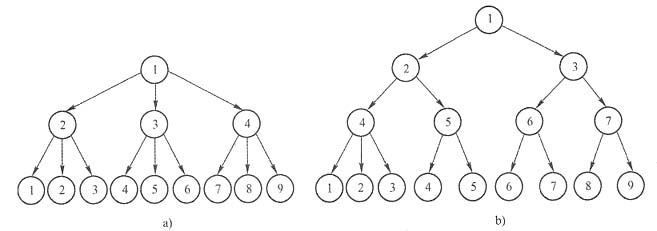 两种结构
两种结构 所以,本题的答案为A、C。
三、填空题1. 一个具有3个结点的二叉树可以有______种形态。
5
[考点] 二叉树
[解析] 这5种形态如下图所示。
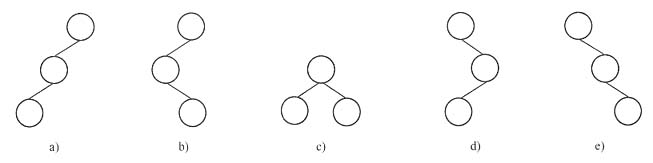 3个结点的二叉树形态
3个结点的二叉树形态
2. 把4000个结点组成一棵二叉树,最小深度是______。
12
[考点] 二叉树
[解析] 要使得二叉树的深度最低,那么就需要把二叉树每一层都排满,即排成一个完全二叉树,深度为k的完全二叉树最多有2^k-1个结点。当k=11时,2^k-1=2047<4000,当k=12时,2^k-1=4095>4000。因此,树的最低深度为12,且最后一层结点的个数为4000-2017=1983。
3. 由权值分别为3、8、6、2、5的叶子结点生成一棵哈夫曼树,它的带权路径长度为______
53
[解析] 根据哈夫曼树的构造算法得到的这个序列的一个哈夫曼树如下图所示。
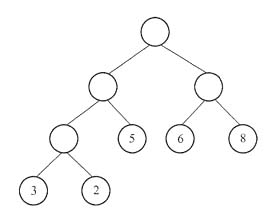 哈夫曼树
哈夫曼树 树的带权路径长度为树中所有叶子结点的带权路径长度和,这棵树的带权路径长度为:3×3+2×3+5×2+6×2+8×2=53。
4. 123456789101112…2014除以9的余数是______
1
[考点] 逻辑题 数学计算
[解析] 123456789101112…2014可以被分解为以下形式:1×10^n+2×10^(n-1)+…+2014(①式)。而10^m-1(m为自然数)都可以被9整除,一个能够被9整除的数具有这样一个特点:各个数位上的数字之和能被9整除,可以使用1×9999…9(共n-1个9)+2×9999…9(共n-2个9)+…+2013×9(②式)来表示一个能够整除9的数。用①式减掉②式之后,其余数不变,结果为1+2+…+2014,所以,本题的问题就转换为求1~2014的和除以9得到的余数了,而1+2+…+2014=(1+2014)×2014/2=2029105。不能被9整除的数具有这样一个特点:如果各位数字之和不能被9整除,那么余数就是这个和除以9得到的余数。对于数字2029105而言,2+0+2+9+1+0+5=19;对于19而言,1+9=10;对于10而言,1+0=1,所以,2029105%9=1。因此,123456789101112…2014除以9的余数是1。
5. 设有字母序列{Q,D,F,X,A,P,N,B,Y,M,C,W},按二路归并方法对该序列进行一次扫描后的结果为______。
DQFXAPBNMYCW
[考点] 排序算法
[解析] 归并排序是利用递归与分治技术将数据序列划分成越来越小的子序列,再对子序列进行排序,最后再用递归法将排好序的子序列合并成越来越大的有序序列。其中,“归”是递归的意思,即递归地将数组折半分割为多个数组,例如数组[2,6,1,0],会先折半,分为[2,6]和[1,0]两个子数组,然后再折半将数组分割,分为[2]、[6]和[1]、[0]。“并”就是将分开的数组按照从小到大或者从大到小的顺序再放到一个数组中。例如上面的[2]、[6]合并到一个数组中是[2,6],[1]、[0]合并到一个数组中是[0,1],然后再将[2,6]和[0,1]合并到一个数组中,即[0,1,2,6]。
具体而言,二路归并排序算法的原理如下:对于给定的一组记录(假设共有n个记录),首先将数组中的元素两两分组,得到n/2(向上取整)个长度为2或1的有序子序列,对每个分组中的元素进行排序,再将其两两归并,反复执行此过程,直到得到一个有序序列为止。
对于本题而言,一次扫描后的结果为: