第Ⅰ部分 (选择题)
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)2. 函数

在点x=0处连续,则k等于______
A.

B.0
C.

D.

A B C D
D
[考点] 分段函数在一点处的连续性.
[解析]

因为f(x)在x=0连续,所以

,即

.
5. 设
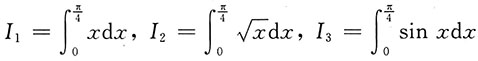
,则______
- A.I3>I1>I2
- B.I1>I2>I3
- C.I1>I3>I2
- D.I2>I1>I3
A B C D
D
[考点] 定积分的性质.
[解析] 在
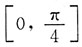
上.
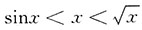
,所以
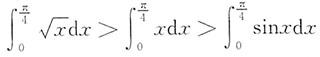
,所以I
2>I
1>I
3.故选D.
7. 设
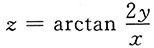
,则
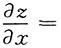
______
A.
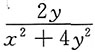
B.
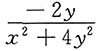
C.
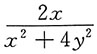
D.
A B C D
B
[考点] 二元函数的偏导数.
[解析] 因为
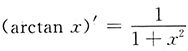
,所以
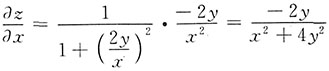
.
8. 方程z=3x
2+3y
2表示的曲面是______
A B C D
B
[考点] 简单的二次曲面所对应的标准方程.
[解析] 绕z轴旋转而得的旋转抛物面的方程为:x
2+y
2=2pz,所以z=3x
2+3y
2表示的曲面为旋转抛物面;球面方程为:(x-a)
2+(y-b)
2+(z-c)
2=R
2;椭球面方程为:
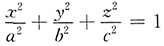
;圆锥面方程为:
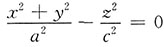
.
第Ⅱ部分 (非选择题)
二、填空题1.

[考点] 洛必达法则.
[解析]

2. 设f(x)在x=1处连续,且
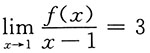
,则f'(1)=______.
3
[考点] 未定式的极限及导数定义.
[解析] 由题设条件
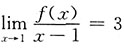
,但
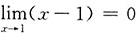
,故必有
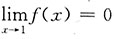
,又f(x)在x=1处连续,故
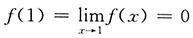
,所以由导数定义

.
3. 设曲线y=f(x)在点(2,f(2))处的切线平行于x轴,则该切线方程为______.
y=f(2)
[考点] 曲线上一点处的切线方程.
[解析] 因为曲线y=f(x)在(2,f(2))处的切线平行于x轴,所以y'(2)=0.即斜率k=0,则此处的切线方程为y-f(2)=0(x-2)=0,即y=f(2).
5. 求
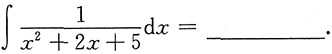
[考点] 不定积分的计算.
[解析]
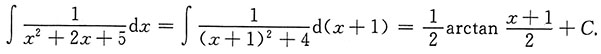
6.
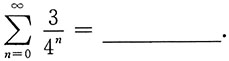
4
[考点] 数项级数的和.
[解析]
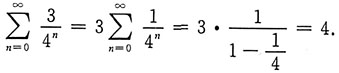
7. 设z=x
4+2y
2,则dz=______.
4x3dx+4ydy
[考点] 二元函数的全微分.
[解析] zx=4x3,zy=4y,所以dz=zxdx+zydy=4x3dx+4ydy.
8. 设区域D由y轴,y=x,y=1所围成,则

[考点] 二重积分的计算.
[解析]

9. 设y
1(x),y
2(x)是二阶常系数线性微分方程y"+py'+qy=0的两个线性无关的解,则它的通解为______.
y=C1y1(x)+C2y2(x)(C1,C2为任意常数)
[考点] 二阶常系数齐次线性方程的通解.
[解析] 通解为y=C1y1(x)+C2y2(x),其中C1,C2为任意常数.
10. 设平面π的方程为x-y+2z=1,则过点A(2,-1,2)且与平面π垂直的直线方程为______.
[考点] 空间直线的标准方程.
[解析] 平面的法向量为{1,-1,2}.
所以直线方程为

三、解答题(共70分。解答应写出推理、演算步骤)1. 计算

2. 设
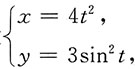
求
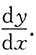
所给问题为参数方程求导问题.由于
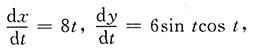
因此
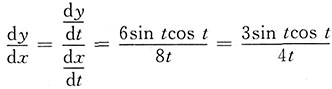
.
[考点] 由参数方程确定的函数的求导方法.
3. 设函数
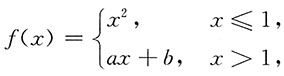
式确定a,b的值,使f(x)在点x=1处既连续又可导.
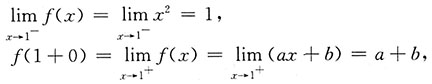
因f(x)在x=1处连续,
故a+b=1,b=1-a.
又
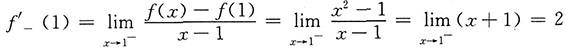
,

,
要使f(x)在x=1处可导,必须f'
-(1)=f'
+(1),
故a=2.于是b=1-a=-1.
所以,当a=2,b=-1时,函数f(x)在点x=1处既连续又可导.
[考点] 分段函数在一点处的连续性和可导性.
4. 计算
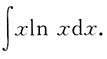
5. 求方程(y-x
2y)y'=2x的通解.
分离变量得
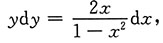
两边积分得
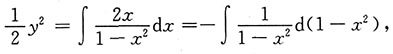
即
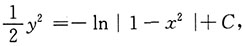
或y
2=-2ln|1-x
2|+C.
[考点] 利用分离变量法求一阶微分方程的通解.
6. 求幂级数
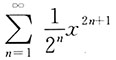
的收敛区间.
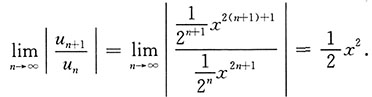
当
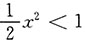
,即x
2<2时,所给级数收敛,因此,收敛区间为
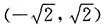
.
[考点] 幂级数的收敛区间.
7. 求过点M
0(0,3,2),且与两个平面π
1,π
2都平行的直线方程,其中
π
1:x+y-2z-1=0,
π
2:x+2y-z+1=0.
平面π
1的法向量n1={1,1,-2},平面π
2的法向量n
2={1,2,-1},
设直线的方向向量s={x,y,z},由题意知,s⊥n
1且s⊥n
2,
所以有:
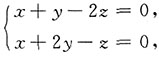
得
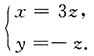
即直线的方向向量为{3,-1,1},直线方程为:
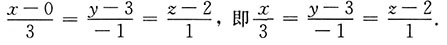
[考点] 空间直线的标准方程.
8. 计算
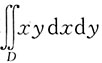
,其中D由y=x,y=1与y轴围城.
解法1
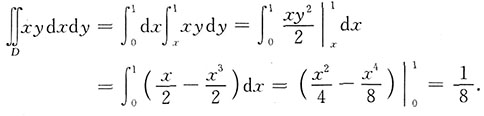
解法2
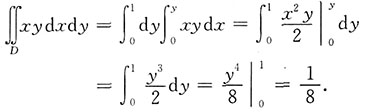
[考点] 二重积分的计算.