一、单项选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)2. 曲线y=x
4-2x
3的凸区间为______
A.(-∞,0],[1,+∞)
B.[0,1]
C.
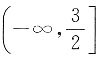
D.

A B C D
A
[考点] 导数计算及应用——导数应用.
[解析] y'=4x3-6x2,y"=12x2-12x,令y"=0,得x1=0,x2=1,当x∈(-∞,0]∪[1,+∞),y">0为凸区间.
4. 已知函数z=z(x,y)由方程z
3-3yz+x
3-2=0所确定,则
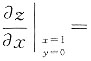
______
A B C D
A
[考点] 偏导数及余微分运算.
[解析] 当x=1,y=0代入方程解z=1对方程x求偏导.
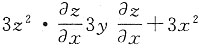
=0,代入x=1,y=0,得
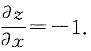
6. 下列级数发散的是______
A.
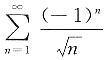
B.
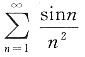
C.
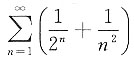
D.

A B C D
D
[考点] 级数——一般项级数分散.
[解析] 选项A交错级数,根据莱布尼兹判定定理A收敛,选项B的上部分收敛,下部分为P级数,次数大于1故收敛,选项C,
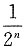
为收敛的几何函数.因为q
n:0<q<1,
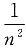
为P级数
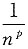
,p>1收敛,故两者之和仍为收敛.
D选项:2
n为几何级数且q
n<1<q,故发散
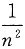
为P级数收敛.
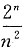
可写成
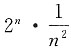
收敛级数与发散级数之积仍为发散级数,故D项为发散.
二、填空题1. 曲线
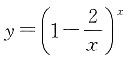
的水平渐近线的方程为______.
y=e-2
[考点] 极限运算——极限渐近线的判断
[解析]
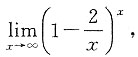
令t=-x,则当x→∞时,t→∞于是
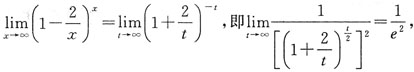
即y=e
-2.
2. 设函数f(x)=ax
3-9x
2+12x在x=2处取得极小值,则f(x)的极大值为______.
5
[考点] 导数计算及应用——求极值.
[解析] f'(x)=3ax2-18x+12
f'(2)=12a-36+12=0
a=2.
令f'(x)=6x2-18x+12=0,
即x2-3x+2=0,(x-1)(x-2)=0.
x1=1,x2=2,令x=1代入,原式f(x)=5.
3. 定积分
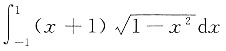
的值为______.
[考点] 定积分的运算.
[解析]
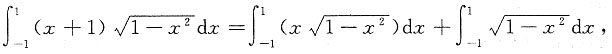
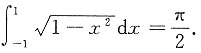
对于
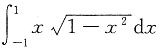
可知其值为0,其结果为

4. 函数

的全微分dz=______.
[考点] 全微分的计算.
[解析]
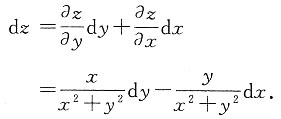
5. 设向量a=(1,2,1),b=(1,0,-1),两向量a+b与a-b的夹角为______.
[考点] 向量与空间解析几何——向量夹角
[解析] a+b=(2,2,0),a-b=(0,2,2),
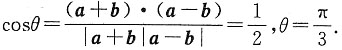
6. 幂级数
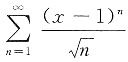
的收敛域为______.
[0,2)
[考点] 级数——一般项级数分散判别
[解析] 令
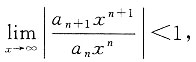
则
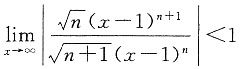
|x-1|<1.
即0<x<2.
把0代入原函数得
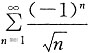
莱布尼兹定理收敛,x=2代入原式发散,故收敛域[0,2).
三、计算题(每小题8分,共64分)1.
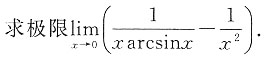
2. 设函数y=f(x)由参数方程
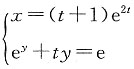
所确定,求

5. 求平行于x轴且经过两点M(1,1,1)与N(2,3,4)的平面方程.
平行于x轴,所以竖法向量N垂直x轴得N在x上的投影为0,所以可设其方程为By+Cz+D=0,则有B+C+D=0,3B+4C+D=0,
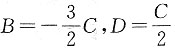
代入后式
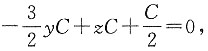
即3y-2z=1.
[考点] 矢量与空间解析几何——空间平面方程.
6. 设z=f(sinx,x
2-y
2),其中函数f具有二阶连续偏导数,求
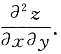
-2ycosxf"12-4xyf"22
[考点] 多元函数微分学——二阶偏导数的计算.
7. 计算二重积分

其中D为由三直线y=-x,y=1,x=0所围成的平面区域.
如图
可得二重积分式
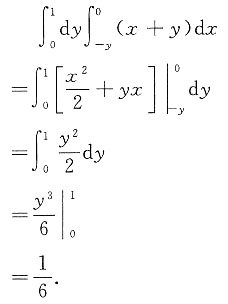
[考点] 二重积分的计算.
8. 求微分方程y"-2y'=xe
3x的通解.
所解方程是二阶常系数非齐次线性微分方程,且f(x)是p
m(x)e
λx型,所验方程对应齐次方程为y"=2y'=0.
它的特征方程为
r
2-2r=0.
有两个根r
1=0,r
2=2于是所得方程对应的齐次方程的通解为
=C
1+C
2e
2x 因f(x)=xe
3x,λ=3不是特征方程的根.
故可设y
*=(ax+b)e
3x y
'*=ae
3x+3(ax+b)e
3x y
"*=3ae
3x+3ae
3x+9(ax+b)e
3x =6ae
3x+9(ax+b)e
3x.
分别代入方程左边得
6ae
3x+9(ax+b)e
3x-2ae
3x-6(ax+b)e
3x=xe
3x 4ae
3x+3(ax+b)e
3x=xe
3x.
经整理(4a+3b)e
3x+3axe
3x=ze
3x.
即
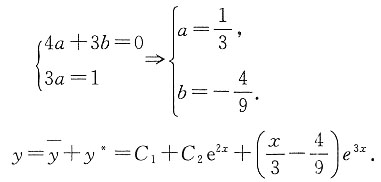
[考点] 常系数非齐次线性微分方程.
四、证明题(每小题9分,共18分)1. 证明:方程xlnx=3在区间(2,3)内有且仅有一个实根.
证明:令f(x)=xlnx-3
因为f'(x)在区间(2,3)内均小于0,
所以f(x)在(2,3)单调递减.
又因为f(2)<0,f(3)>0,
所以xlnx=3在区间(2,3)内有且仅有一个实根.
[考点] 零点定理证明根个数.
2. 证明:当x>0时,
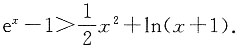
证明:令f(x)=e
x-1-
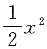
-ln(x+1)
f(0)=0.
因为f'(x)=e
x-x-
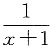
且f'(0)=0,
又因为f"(x)=e
x-1+
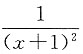
,
当x>0时,f"(x)>0.
所以f'(x)在(0,+∞)单调递增,f'(x)>0.
所以f(z)在(0,+∞)单调递增,f(x)>0.
所以
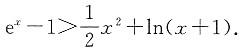
[考点] 通过导数单调性证明不等式.
五、综合题(每小题10分,共20分)1. 设平面图形D由抛物线y=1-x
2及其在点(1,0)处的切线以及y轴所围成,试求:
(1)平面图形D的面积;
(2)平面图形D绕y轴旋转一周所形成的旋转体的体积.
(1)根据已知条件如图所示
y'=-2x在点(1,0)处斜率k=-2,
设切线为y=-2x+2,
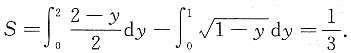
(2)由(1)中的结果得到
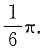
[考点] 定积分的应用——求旋转体体积,求面积.
2. 设φ(x)是定义在(-∞,+∞)上的连续函数,且满足方程

(1)求函数φ(x)的解析式;
(2)讨论函数
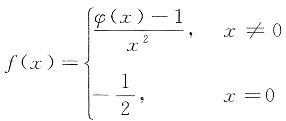
在x=0处的连续性与可导性.
等式两边求导得
(1)xφ(x)=-φ'(x),
即xy=-y',
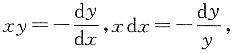
两端积分
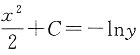
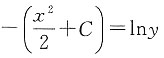
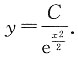
因为原式y(0)=1,
所以C=1.
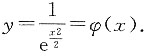
[考点] 定积分的应用,导数定义的应用,函数连续性的判定,导数可导性的判定.
(2)因为
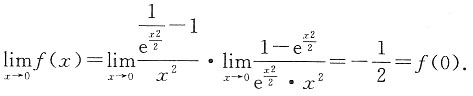
所以f(x)在x=0处为连续.
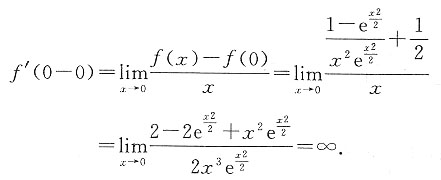
同理f(0+0)=∞根据导数定义设函数不可导.