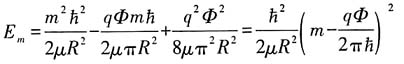解答题1. 利用H-F定理确定氢原子本征态下
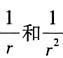
的平均值,并讨论氢原子能级的相对论修正;
解:氢原子哈密顿量

能量本征值为
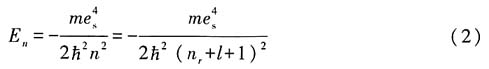
取参量为电荷
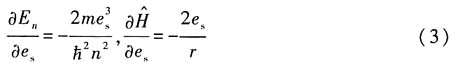
取参量为量子数和量子数l
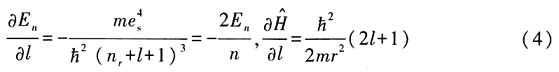
利用式(3)式、(4)式和H-F定理可得
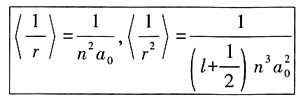
其中
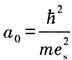
为玻尔半径,所以
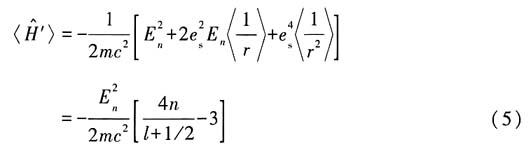
结果表明:相对论修正后的氢原子能量不但依赖于主量子数,还依赖于角量子数.
2. 对于核电荷为Ze的类氢原子,计算处于束缚态下
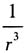
的平均值
解:将角动量分离变量后,类氢原子的等效一维哈密顿量为
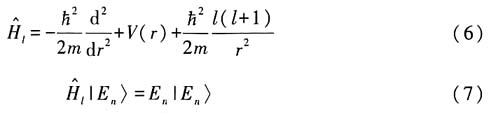
(7)式两边对径向r求导,
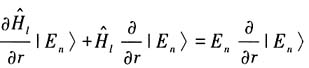
,左乘〈E
n|可得
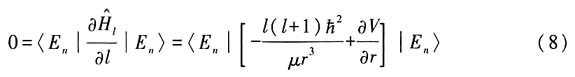
所以
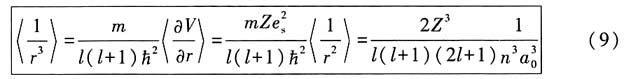
 势场中运动.
势场中运动.3. 用变分法求基态能量时,在x>0区域内的试探波函数应取下列函数中的哪一个?为什么?
(a)x+λx
2,(b)e
-λz2,(c)ze
-λz,(d)sinλz.
解:由题意知,这是束缚态问题,故合适的波函数需要满足:连续、有限性条件,从势函数特征知,在z<0时波函数应为零,另外在无穷远处,波函数应该为零,只有ze-λz满足这些条件.
4. 算出基态能量.
解:取
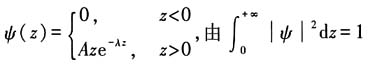
知归一化因子A=2λ
3/2.
下面计算动能和势能在尝试波函数下的平均值,易于算出
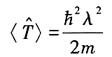
势能平均值
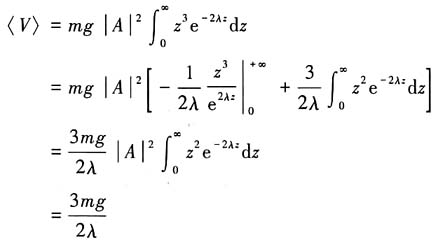
故有
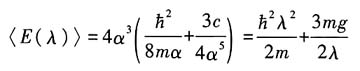
由取极值条件
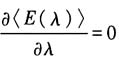
可得
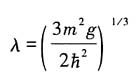
因此估计的基态能量为
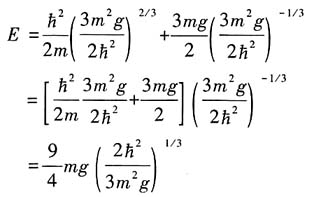
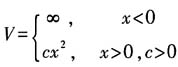 中运动.
中运动.5. 试利用变分法估计体系基态能量(试探波函数可取正比于xe
-αx,α为变分参量);
解:方法一:利用Rayleigh-Ritz变分原理,计算〈E(α)〉
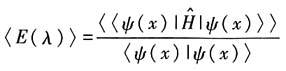
取
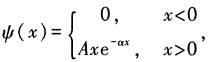
由归一化条件〈ψ|ψ〉=1可得
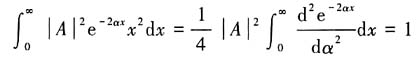
解得A=2α
3/2 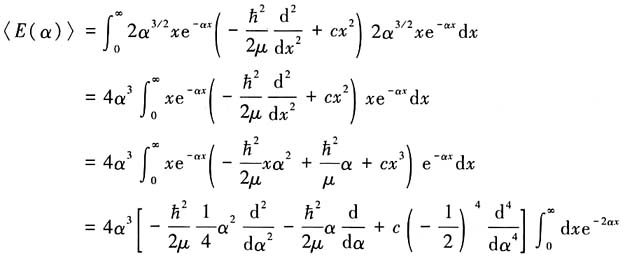
因为
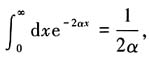
所以
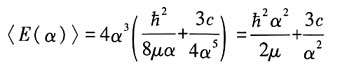
利用
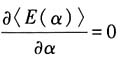
可得
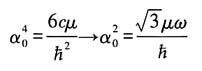
其中
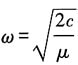
.此时:

方法二:动能平均值处理
转化导数计算为代数运算.
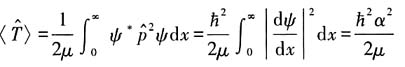
6. 它是精确解的上限还是下限?你能给出精确的基态能量吗?
解:上限.
由边界条件x→0,ψ→0可得:对称谐振子的奇宇称波函数将是半振子解(能量量子数取奇数),基态相当于对称谐振子的第1激发态:
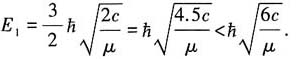
7. 设试探波函数为ψ(x)=e
-λ|x|(λ>0),试用变分法计算一维谐振子的基态能量,并解释与严格解差异的主要来源.
解:注意到波函数未归一化,利用归一化条件可得

计算动能的平均值如下:
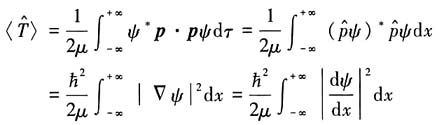
尽管
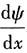
在x=0处不连续,但是
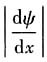
在x=0处连续,故可以继续计算下去.

计算势能的平均值如下:
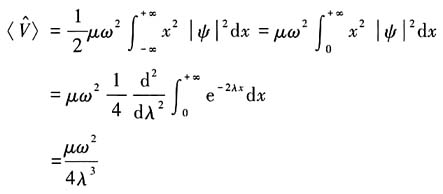
故有:
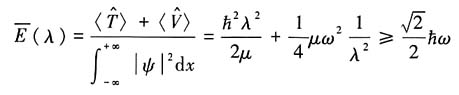
上式中当
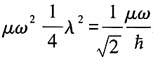
取等号(通过对参数λ求导等于零得到).
与严格解差异的主要来源是波函数对坐标的依赖关系,严格波函数是高斯函数.
8. 质量为μ的粒子在吸引δ势V(x)=-Aδ(x)(A>0)中运动,以谐振子基态型波函数为试探函数,求束缚态的近似能量.
解:谐振子基态型波函数的形式为
ψ(x)=Ne
-αx2 (1)
其中α为变分参量.
粒子在势场中运动的哈密顿量为

能量在试探波函数下的平均值为
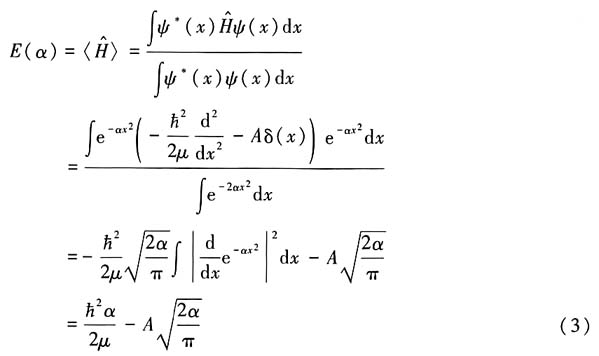
对参数变分求极值
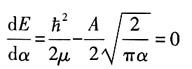
解得

将(4)式代入(3)式得近似能量为
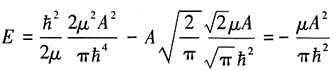
9. 试用变分法求解三维空间如下势阱
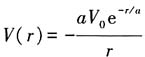
(其中V
0>0,a>0)的质量为μ的粒子的基态能量.试探波函数取为
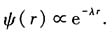
.
解:本题中应特别注意动能平均值在球坐标中的计算.
由题意知:波函数关于角向对称,故对于动能只需要计算径向动能,关于角向部分贡献波函数加上归一化因子即可.
取ψ(r)=Ae
-λr,首先求归一化因子
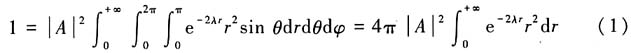
经过分部积分解得:
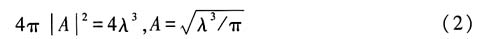
(1)动能平均值计算:
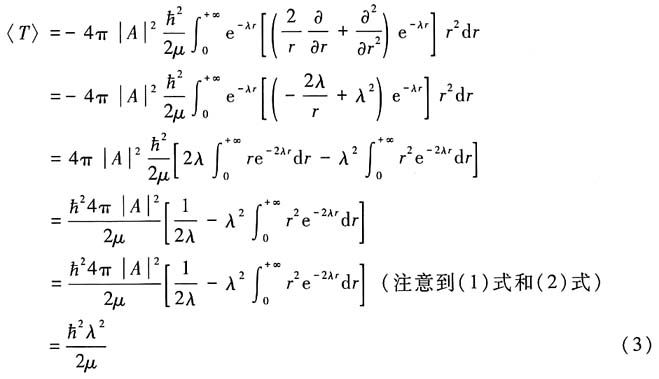
(2)势能平均值计算:
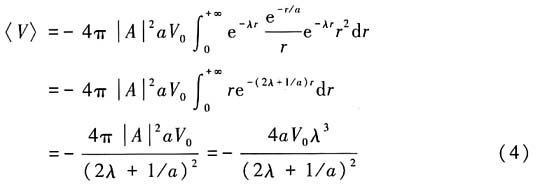
故有在试探波函数下的能量为
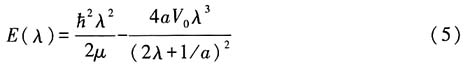
因束缚态能量小于零,因此必须
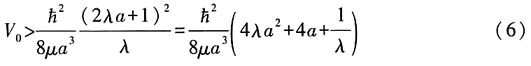
对于束缚态,λ>0,由极值条件可知,当
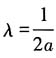
时有V
0极小值,因此

由
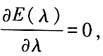
可得
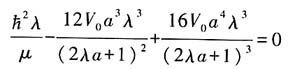
整理得到:
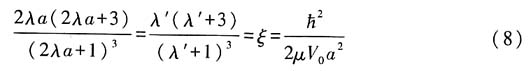
由(7)式和束缚态条件可得:
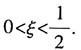
由三阶方程求根公式可以求得能量取极小值时(即基态)的
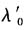
,将其代入(5)式可得基态能量为
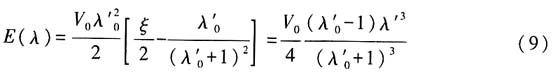
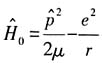 ,基态波函数及基态能量分别为
,基态波函数及基态能量分别为

其中 为第一玻尔轨道半径,设体系受到微扰
为第一玻尔轨道半径,设体系受到微扰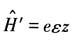 的作用(沿z方向加上均匀电场ε),哈密顿量变为
的作用(沿z方向加上均匀电场ε),哈密顿量变为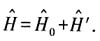
10. 计算对易关系:
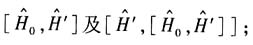
解:
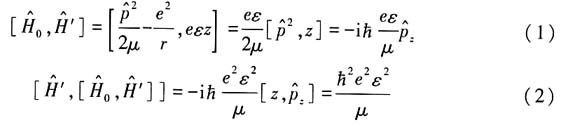
11. 计算ψ
0(r)下的平均值:
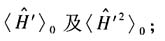
解:
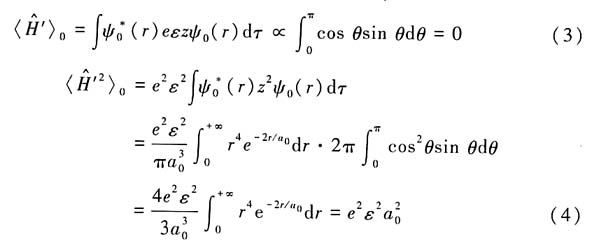
12. 取基态试探波函数为
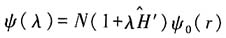
,其中N为归一化常数,试以λ为变分参量,用变分法求
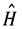
的基态能量上限(准确到ε
2量级).
解:注意到波函数未归一化,所以有
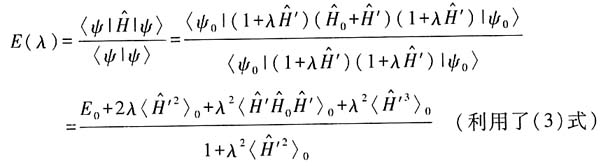
由
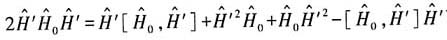
可得
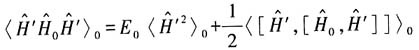
所以有
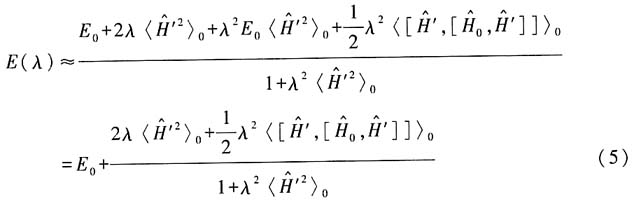
由
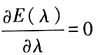
和(2)式、(3)式、(4)式可得
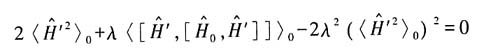
即
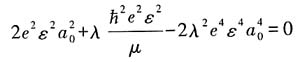
上式忽略四次方项,可得

将(6)式代入(5)式可得,基态近似能量为
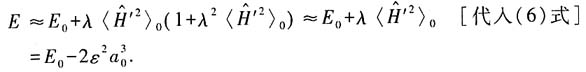
计算中用到了
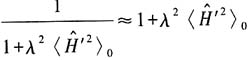
,因为
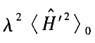
。为小量.
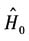 仅有两个本征态,ψa(能量为Ea)和ψb(能量为Eb),它们是正交归一的(假定Ea<Eb).现引入一个微扰
仅有两个本征态,ψa(能量为Ea)和ψb(能量为Eb),它们是正交归一的(假定Ea<Eb).现引入一个微扰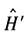 ,具有下列矩阵元
,具有下列矩阵元

其中ε为正的常量,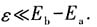
13. 求微扰哈密顿量的严格本征值;
解:由已知条件可得系统的哈密顿量为
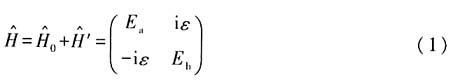
根据久期方程可得

解得
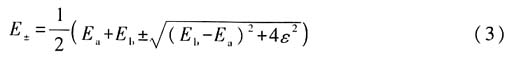
14. 用二次微扰理论估算微扰系统的能量;
解:由非简并微扰论,能量的一级修正为

二级修正为
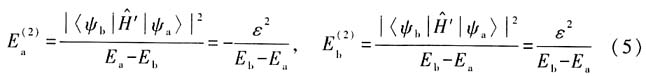
故二级微扰下系统的能量为
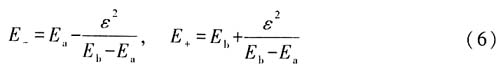
15. 用变分原理估算微扰系统的基态能量,取试探波函数
ψ=cosθψ
a+e
iφsinθψ
b 其中θ,φ是可调参量;
解:题目中试探波函数已经归一化,所以哈密顿量在试探波函数下的平均值为
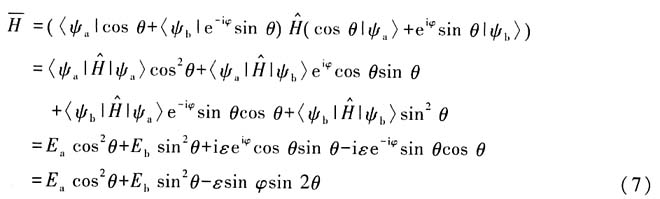
鉴于包含两个参量,需要用到变分

取极小值的条件为

即
(E
b-E
a)sin2θ-28sinφcos2θ=0,cosφ=0 (10)
因此sinφ=1,-1.
讨论:(i)当sinφ=1时,由(10)式可得
tan2θ=2ε/(E
b-E
a)=γ (11)
考虑到
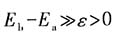
,故可得
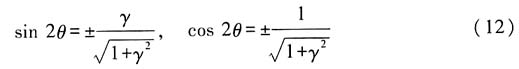
所以
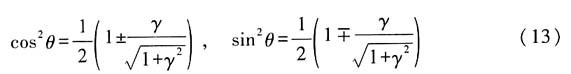
由(7)式可得
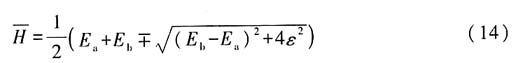
(ii)当sinφ=-1时,由(10)式可得
tan2θ=-2ε/(E
b-E
a)<0 (15)
此时
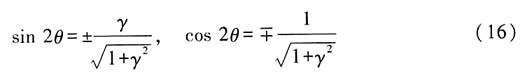
同理可得
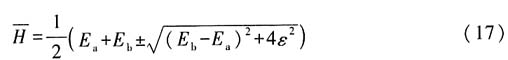
结合(14)式和(17)式可得,由变分法得到的能级表达式与精确解相同.
对于基态,
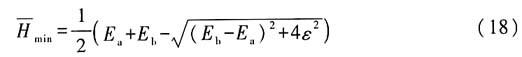
16. 对比第一问、第二问、第三问中计算结果,讨论变分原理得到的结果的准确性.
解:对比第一问和第三问结果可知:变分法得到的能级与精确解完全相同,这是因为题目给出的试探波函数已经是二能级系统的最一般的波函数形式,即写成了H
0的本征态的叠加.由变分法确定的叠加系数正好是精确的基态波函数的叠加系数.
考虑到
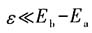
,第一问中的精确解可展开
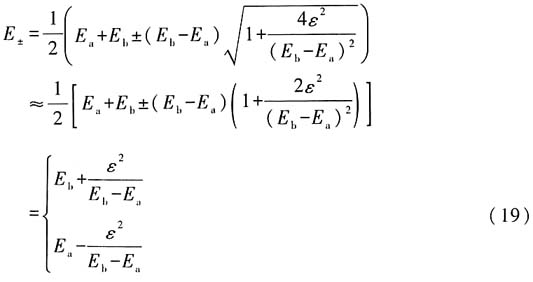
这正是第二问中二级微扰论近似下的结果.
17. 试推导氢原子内部的磁场与轨道角动量之间的表达式
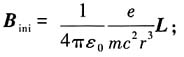
解:氢原子中质子一电子系统,可以看成相对运动.从电子的角度讲,质子在绕着它做圆周运动,形成一个连续的环电流
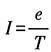
(其中e为元电荷).环电流对环中心的电子产生一个磁场,根据电磁学中毕奥一萨伐尔定律可得

此外,在质子静止坐标系中,电子运动的轨道磁矩

所以有

考虑到L的方向与B的方向一致,所以有
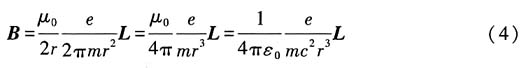
上式中用到了
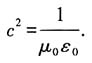
18. 利用第一问中表达式,估算氢原子内部的磁场大小,并定量给出“强”和“弱”的塞曼场的大小;
解:在(4)式中取
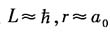
(玻尔半径),则有
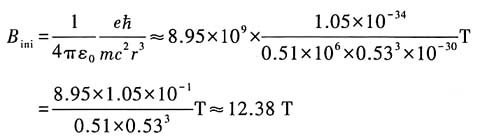
通常所说的外加磁场的强弱是相对原子内磁场来讲的,强塞曼效应对应于远大于原子内磁场的磁场量级,即
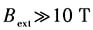
;弱塞曼效应对应于远小于原子内磁场的磁场量级,
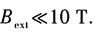
19. 推导出氢原子自旋一轨道耦合的表达式.
解:电子自旋磁矩
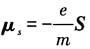
在磁场B中带来的相互作用能量为

由(4)式和(5)式可得
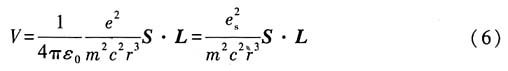
上式是在电子静止坐标系中讨论得到的,需要引入相对论动力学效应进行修正,即乘一个
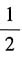
引子.修正后的自旋一轨道耦合能量的表达式为
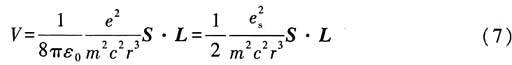
20. 电荷为q、质量为μ的点粒子在沿z方向的均匀恒定磁场B中运动时的哈密顿量为
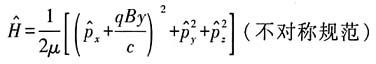
证明:力学量
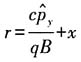
为守恒量.
证明:因为力学量r不显含时间,故只需证明它与系统的哈密顿量对易.
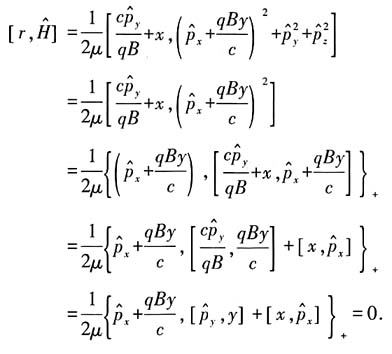
证毕.
21. 外磁场中电子的哈密顿量
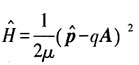
(1)求位置矢量
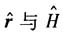
的对易关系
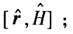
(2)证明:
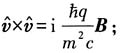
(3)证明连续性方程
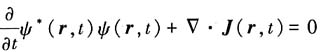
中的概率流密度为
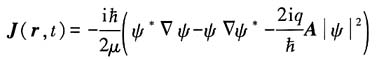
解:
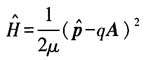
(1)方法一:
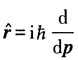
,故
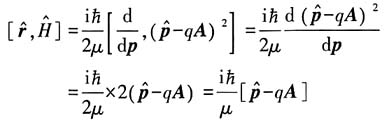
方法二:
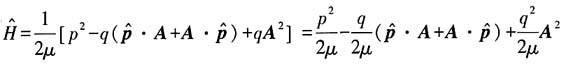
因
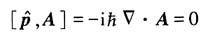
所以
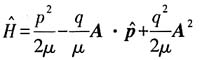
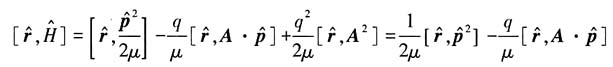
利用坐标与动量间对易关系:
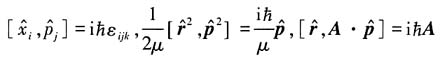
故
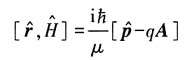
(2)以
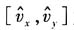
为例进行证明
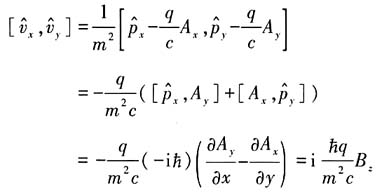
类似有
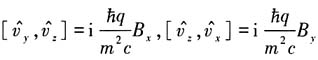
,写成矢量形式即证.
讨论:进一步可得
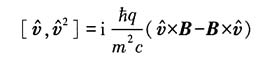
(3)
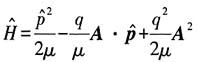
,含时薛定谔方程为
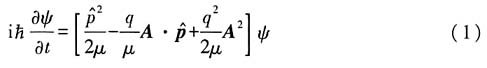
取共轭有(注意到:A为实,
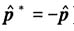
):
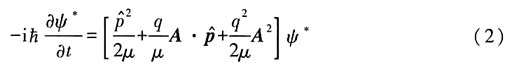
ψ
*×(1)-ψ×(2)得
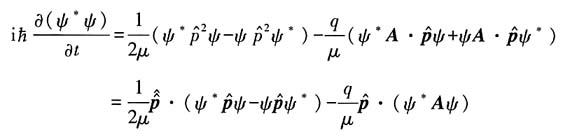
故有
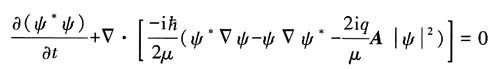
所以
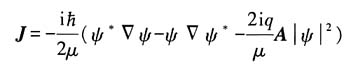
22. 电子在恒定均匀磁场B=Be
z中运动(e
z为z方向单位矢量),同时考虑空间运动与自旋运动:
(1)写出体系的哈密顿量
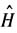
;
(2)求
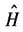
的本征值与本征函数.
解:此题中应该不考虑自旋与轨道间相互作用
(1)
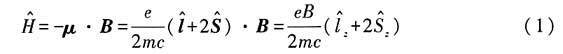
(2)显然自旋角动量与轨道角动量可以分离变量

令ψ=φ(r)χ,代入上式:
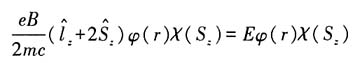
即:
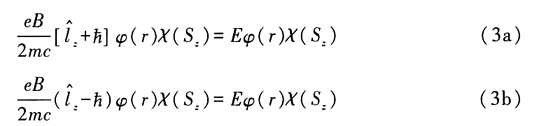
解得:
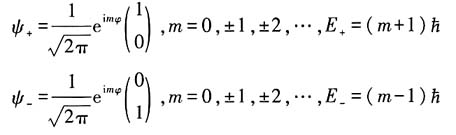
24. 求其能量本征值和本征函数.
解:令
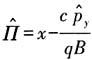
,则有
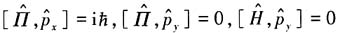
,p
y为守恒量,又设
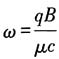
,所以有
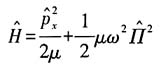
能量的本征值方程为
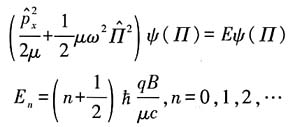
相应的本征函数为
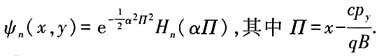
25. 我们可以将半经典的玻尔一索末菲关系
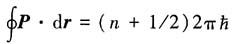
(其中积分沿一封闭的轨道)推广应用到有电磁场存在的情形,只需用p-eA/c代替P.应用这关系及关于线动量p的运动方程,推导一半经典电子在一磁场B中沿任意轨道运动时,其磁通量的量子化条件,对于固体中的电子,这条件可用电子轨道在k空间的尺度S重新加以描述,试找出用B表达的S的量子化条件(忽略自旋效应).
解:在电磁场存在下,正则动量

,其中p为机械动量,由推广的玻尔-索末菲关系,有
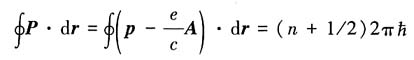
由
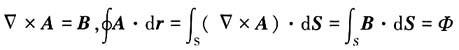
及电子在电磁场中运动
的经典方程式
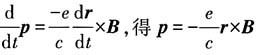
(设B是恒场).则
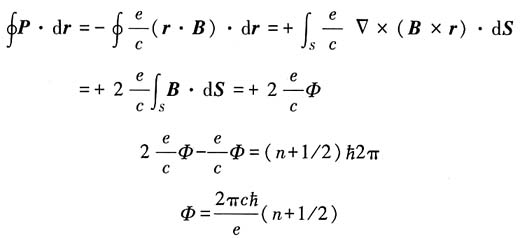
又由
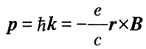
,得
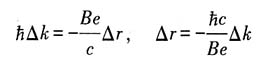
所以轨道在k空间中所占的面积S
n与其在位置空间中的面积A
n之间关系为
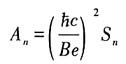
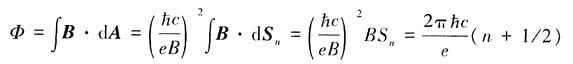
故有
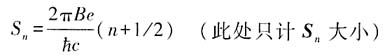
26. 写出这个体系的含时薛定谔方程;
解:
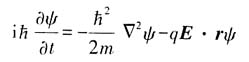
27. 证明当粒子处于任意态ψ(r,t)时,坐标算符的期望值满足牛顿第二定律;
解:

所以
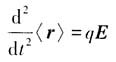
28. 可证明,这一结果在还有一均匀静磁场存在的情况下也正确.这一结论在质谱仪、粒子加速器等仪器的设计中有用吗?试解释之.
解:这一结果使我们在计算仪器中带电粒子的运动轨迹时,可以直接用经典力学处理.
29. 质量μ、荷电q的粒子在方向互相垂直的均匀电场ε和均匀磁场B中的运动,求能量本征值和本征函数.
解:设电磁场分别为ε=(ε,0,0),B=(0,0,B) (1)
取电磁场的标、矢势为

满足关系
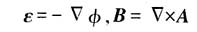
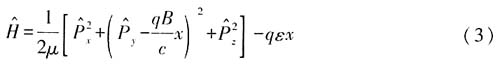
取守恒量完全集为

,它们的共同本征函数可以写成
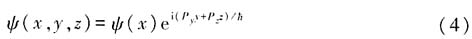
其中P
y和P
z为本征值,可取任意实数.ψ(x,y,z)满足能量本征方程
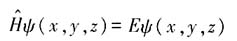
因此ψ(x)满足方程
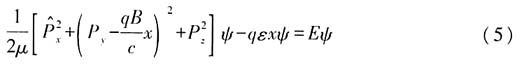
亦即,对于ψ(x)来说,H和下式等价:
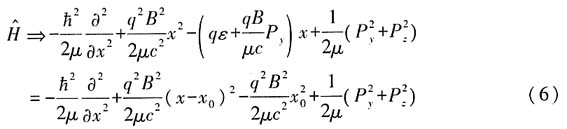
其中
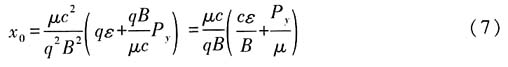
(6)式相当于一维谐振子能量算符
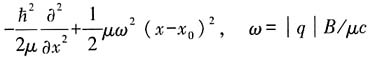
再加上两项常数,因此,本题能级为
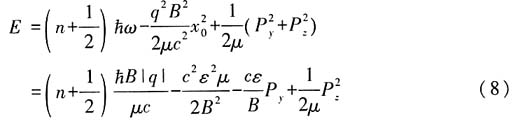
其中P
y,P
z为任意实数,n=0,1,2,….
(4)式中ψ(x)为以(x-x
0)为变量的一维谐振子的能量本征函数,即
ψ(x)=ψ
n(x-x
0)=H
n(ε)e
-ξ2/2 (9)
其中H
n(ξ)为厄米多项式,
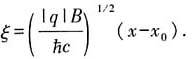
30. 一个带电粒子被限制在半径为R的圆环上运动,其质量为μ,电荷量为q.在圆环中加上磁场,磁通量为Φ,磁场被约束在r<R的区域,此时环上磁场为零,但矢势A不为零
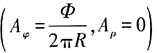
.粒子的哈密顿量可写为
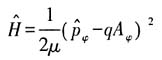
(1)请问能谱是分立的还是连续的?
(2)请求出粒子的能级和波函数.
解:
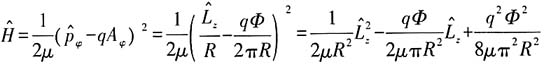
显然
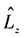
的本征态为系统的本征态,即
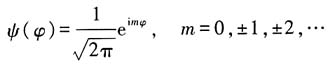
代入定态薛定谔方程
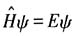
可得
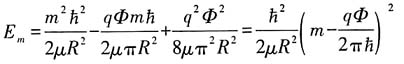
其中m为整数.因此,粒子的能级是分立的.
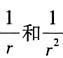 的平均值,并讨论氢原子能级的相对论修正;
的平均值,并讨论氢原子能级的相对论修正;
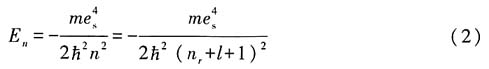
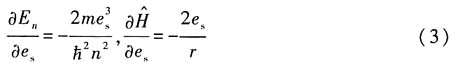
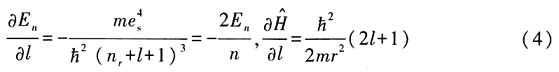
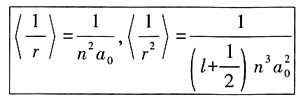
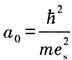 为玻尔半径,所以
为玻尔半径,所以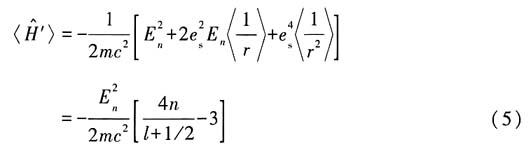
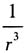 的平均值
的平均值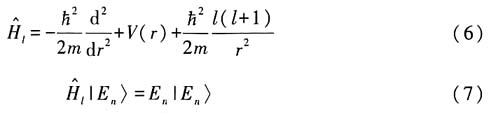
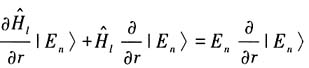 ,左乘〈En|可得
,左乘〈En|可得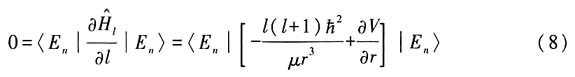
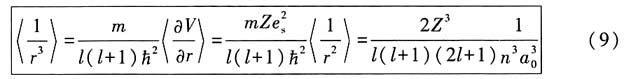
 势场中运动.
势场中运动.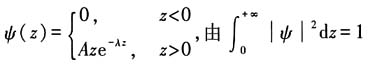 知归一化因子A=2λ3/2.
知归一化因子A=2λ3/2.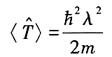
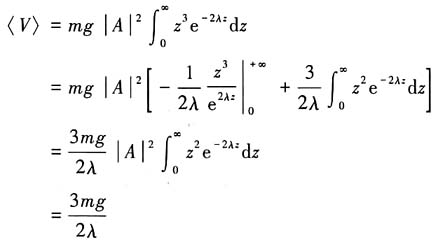
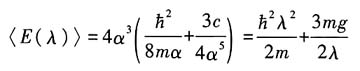
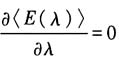 可得
可得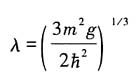
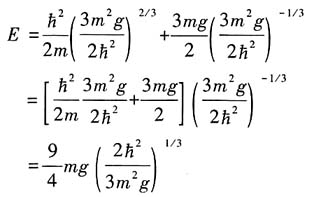
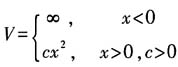 中运动.
中运动.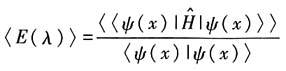
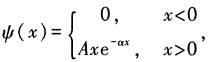 由归一化条件〈ψ|ψ〉=1可得
由归一化条件〈ψ|ψ〉=1可得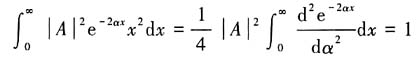
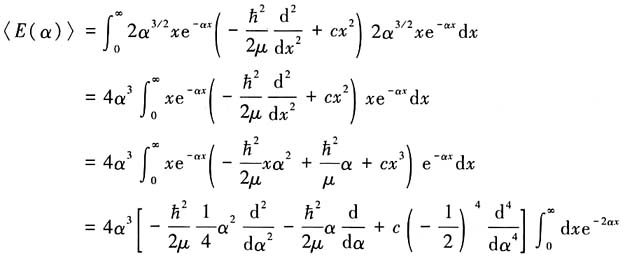
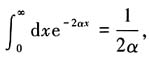 所以
所以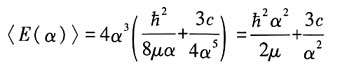
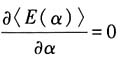 可得
可得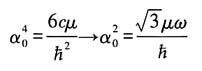
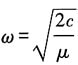 .此时:
.此时:
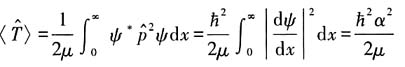
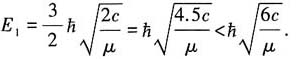

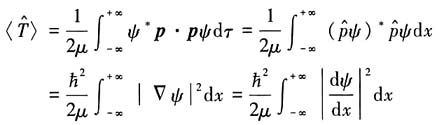
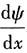 在x=0处不连续,但是
在x=0处不连续,但是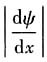 在x=0处连续,故可以继续计算下去.
在x=0处连续,故可以继续计算下去.
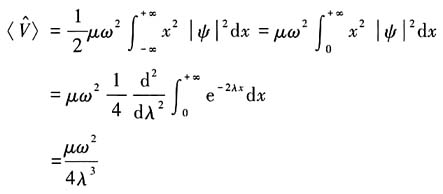
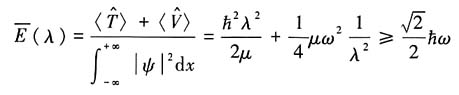
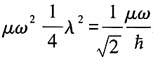 取等号(通过对参数λ求导等于零得到).
取等号(通过对参数λ求导等于零得到).
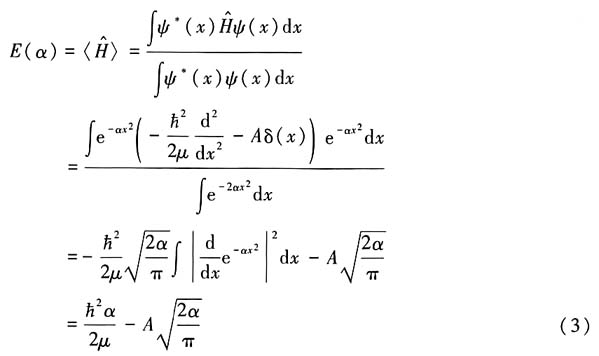
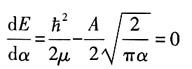

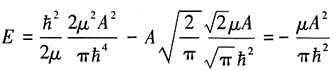
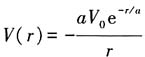 (其中V0>0,a>0)的质量为μ的粒子的基态能量.试探波函数取为
(其中V0>0,a>0)的质量为μ的粒子的基态能量.试探波函数取为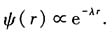 .
.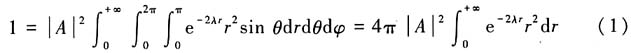
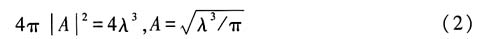
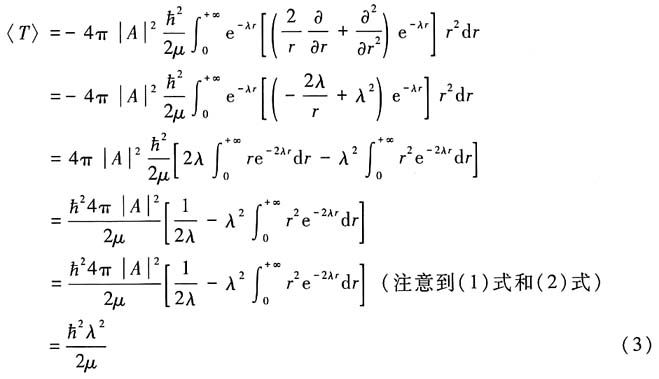
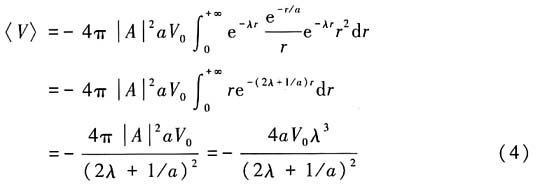
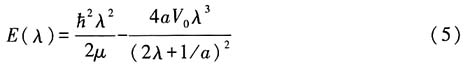
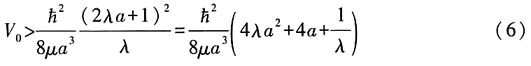
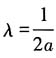 时有V0极小值,因此
时有V0极小值,因此
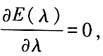 可得
可得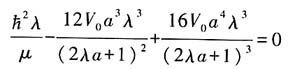
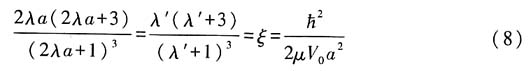
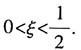
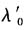 ,将其代入(5)式可得基态能量为
,将其代入(5)式可得基态能量为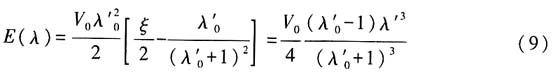
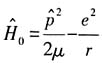 ,基态波函数及基态能量分别为
,基态波函数及基态能量分别为
 为第一玻尔轨道半径,设体系受到微扰
为第一玻尔轨道半径,设体系受到微扰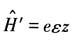 的作用(沿z方向加上均匀电场ε),哈密顿量变为
的作用(沿z方向加上均匀电场ε),哈密顿量变为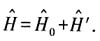
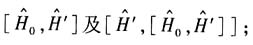
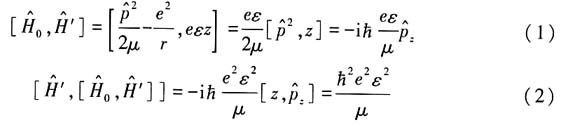
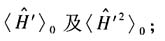
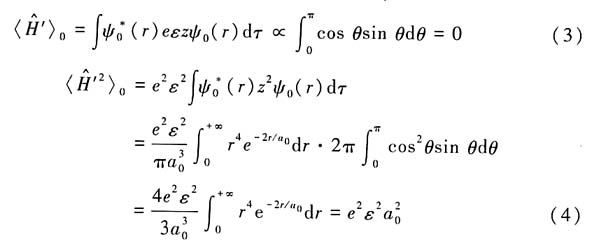
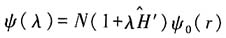 ,其中N为归一化常数,试以λ为变分参量,用变分法求
,其中N为归一化常数,试以λ为变分参量,用变分法求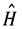 的基态能量上限(准确到ε2量级).
的基态能量上限(准确到ε2量级).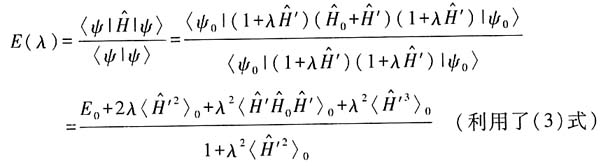
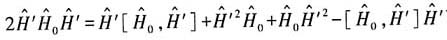 可得
可得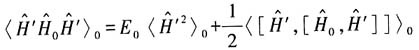
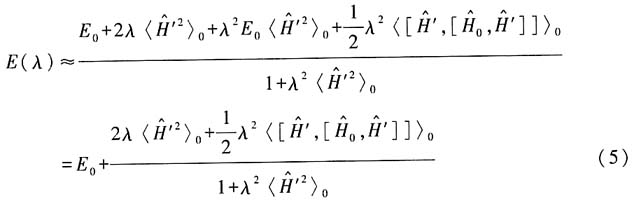
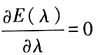 和(2)式、(3)式、(4)式可得
和(2)式、(3)式、(4)式可得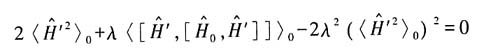
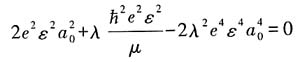

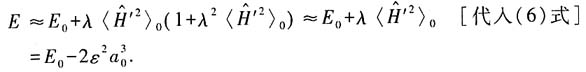
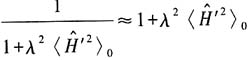 ,因为
,因为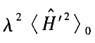 。为小量.
。为小量.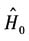 仅有两个本征态,ψa(能量为Ea)和ψb(能量为Eb),它们是正交归一的(假定Ea<Eb).现引入一个微扰
仅有两个本征态,ψa(能量为Ea)和ψb(能量为Eb),它们是正交归一的(假定Ea<Eb).现引入一个微扰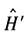 ,具有下列矩阵元
,具有下列矩阵元
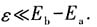
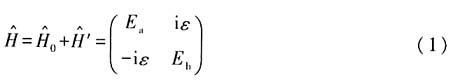

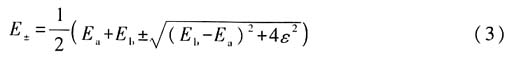

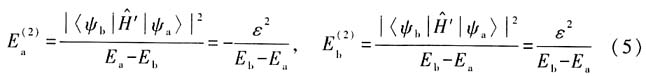
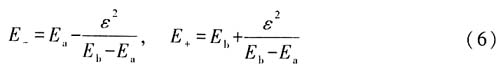
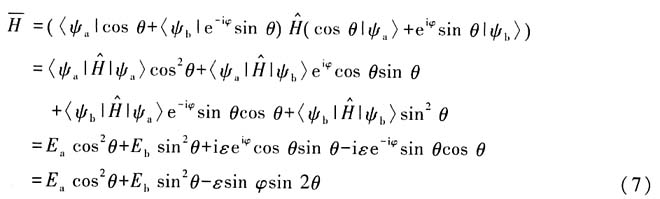


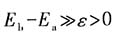 ,故可得
,故可得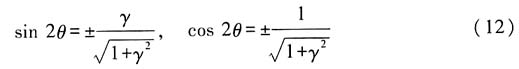
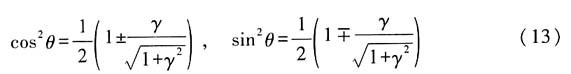
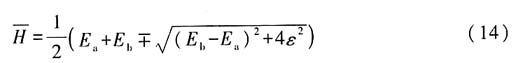
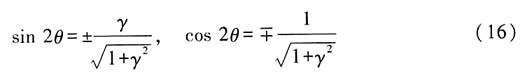
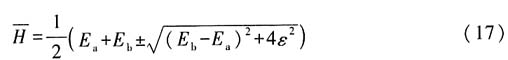
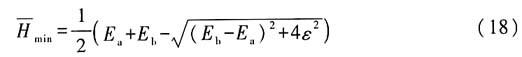
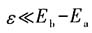 ,第一问中的精确解可展开
,第一问中的精确解可展开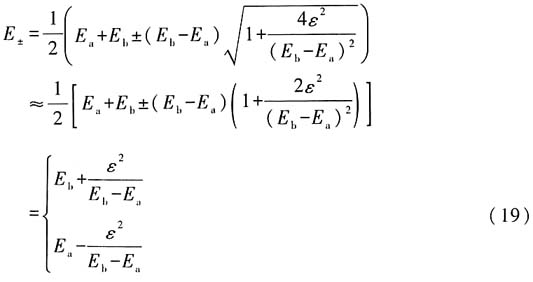
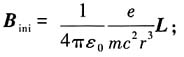
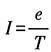 (其中e为元电荷).环电流对环中心的电子产生一个磁场,根据电磁学中毕奥一萨伐尔定律可得
(其中e为元电荷).环电流对环中心的电子产生一个磁场,根据电磁学中毕奥一萨伐尔定律可得


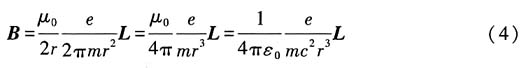
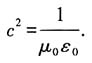
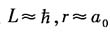 (玻尔半径),则有
(玻尔半径),则有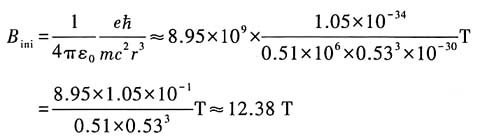
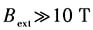 ;弱塞曼效应对应于远小于原子内磁场的磁场量级,
;弱塞曼效应对应于远小于原子内磁场的磁场量级,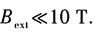
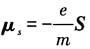 在磁场B中带来的相互作用能量为
在磁场B中带来的相互作用能量为
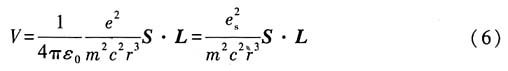
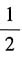 引子.修正后的自旋一轨道耦合能量的表达式为
引子.修正后的自旋一轨道耦合能量的表达式为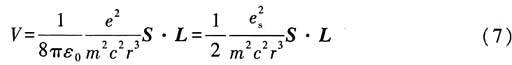
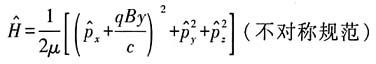
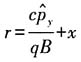 为守恒量.
为守恒量.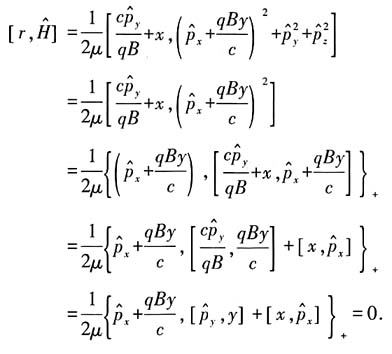
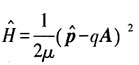
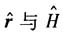 的对易关系
的对易关系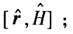
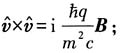
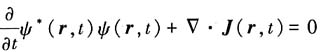 中的概率流密度为
中的概率流密度为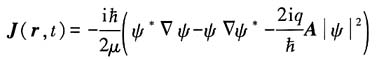
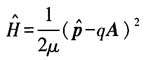
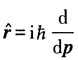 ,故
,故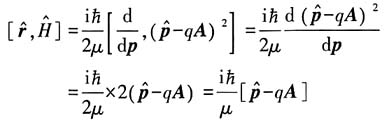
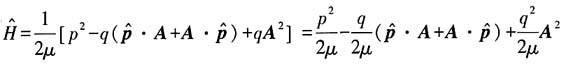
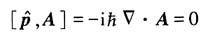
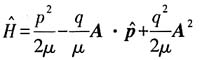
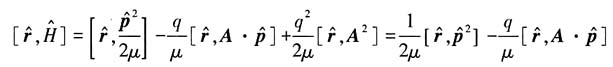
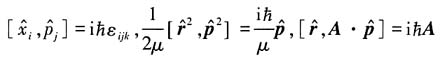
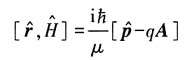
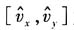 为例进行证明
为例进行证明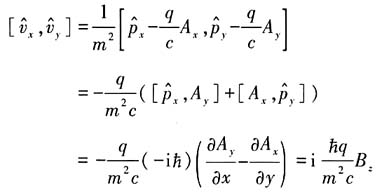
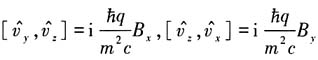 ,写成矢量形式即证.
,写成矢量形式即证.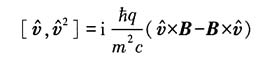
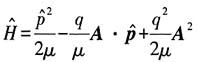 ,含时薛定谔方程为
,含时薛定谔方程为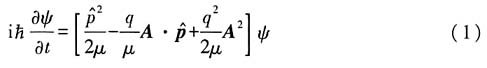
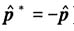 ):
):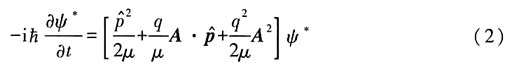
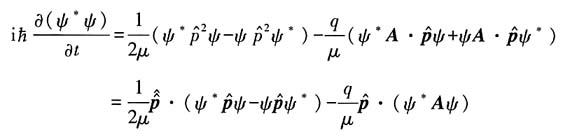
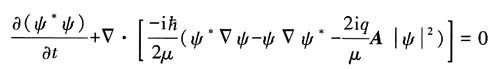
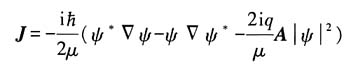
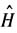 ;
;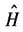 的本征值与本征函数.
的本征值与本征函数.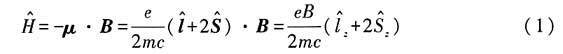

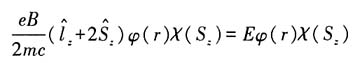
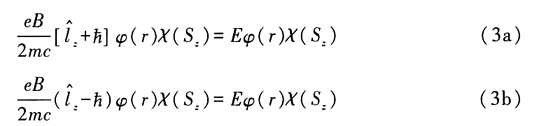
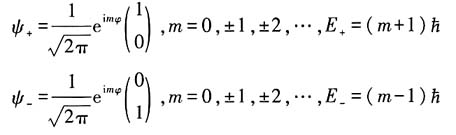
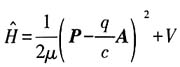 ,因为
,因为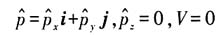

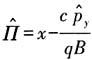 ,则有
,则有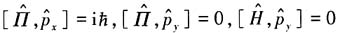 ,py为守恒量,又设
,py为守恒量,又设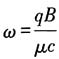 ,所以有
,所以有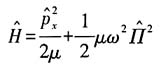
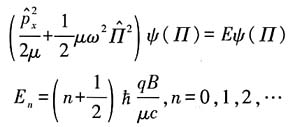
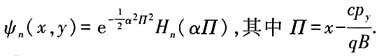
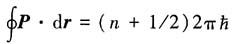
 ,其中p为机械动量,由推广的玻尔-索末菲关系,有
,其中p为机械动量,由推广的玻尔-索末菲关系,有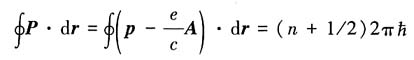
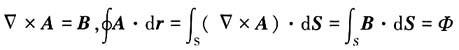 及电子在电磁场中运动
及电子在电磁场中运动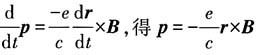 (设B是恒场).则
(设B是恒场).则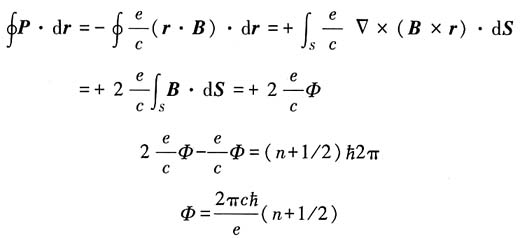
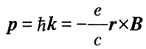 ,得
,得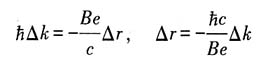
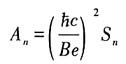
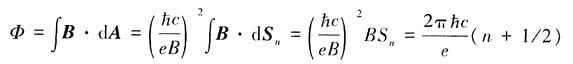
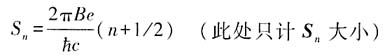
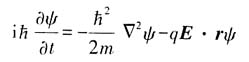

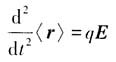

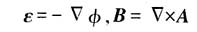
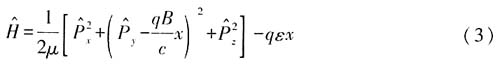
 ,它们的共同本征函数可以写成
,它们的共同本征函数可以写成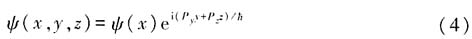
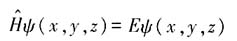
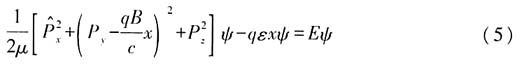
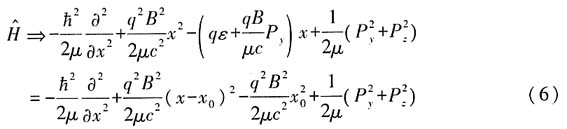
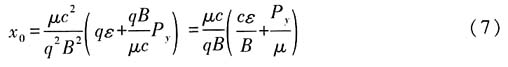
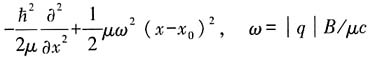
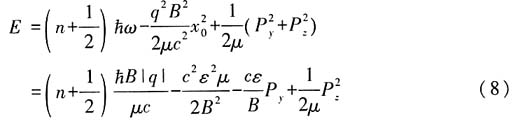
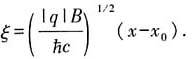
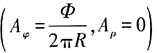 .粒子的哈密顿量可写为
.粒子的哈密顿量可写为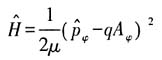
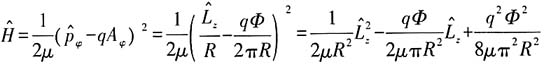
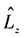 的本征态为系统的本征态,即
的本征态为系统的本征态,即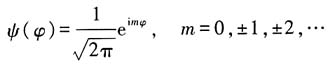
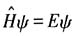 可得
可得