一、单项选择题(在每小题给出的四个备选项中,选出一个正确的答案)5.
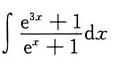
=______
A.e
2x+e
x+x+C
B.
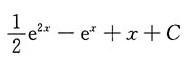
C.
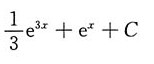
D.
A B C D
B
[解析]
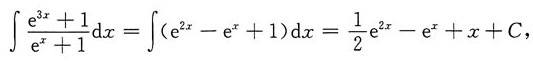
故选B.
6. 曲线y=x
2与直线y=1所围成的图形的面积为______
A.
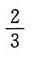
B.
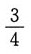
C.
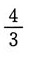
D.1
A B C D
C
[解析] 方法一
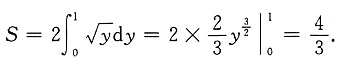
方法二
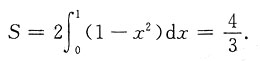
8. 下列方程中为可分离变量方程的是______
- A.y'=exy
- B.xy'+y=ex
- C.(x-xy2)dx+(y+x2y)dy=0
- D.yy'+y+x=0
A B C D
C
[解析] 由(x-xy
2)dx+(y+x
2y)dy=0,得x(1-y
2)dx+y(1+x
2)dy=0,y(1+x
2)dy=x(y
2-1)dx,所以
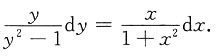
故选C.
9. 已知向量组α
1=(1,0,2,3)
T,α
2=(1,1,3,5)
T,α
3=(1,-1,a+2,1)
T的秩为2,则a=______
A B C D
C
[解析]
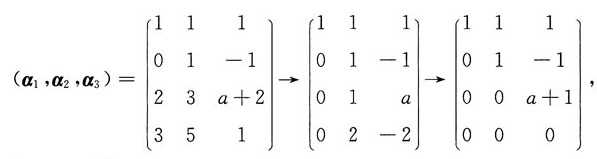
,若r(α
1,α
2,α
3)=2,则a+1=0,即a=-1.
10. 下列级数发散的是______
A.
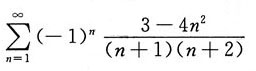
B.
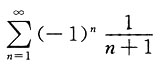
C.
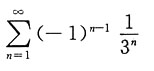
D.
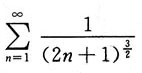
A B C D
A
[解析] 由于
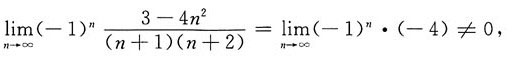
则
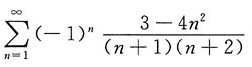
发散,故选A.
二、填空题1. 若函数
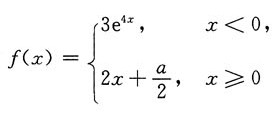
在x=0处连续,则a=______.
6
[解析]
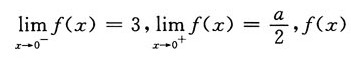
在x=0处连续,所以
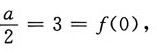
解得a=6.
2.
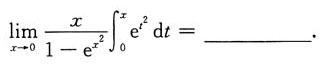
-1
[解析]
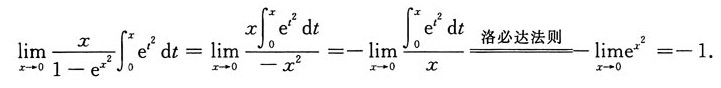
3. 设A为m阶矩阵,若已知|A|=3,则|-mA|=______.
3(-m)m
[解析] |-mA|=(-m)m|A|=3(-m)m.
4. 已知函数f(x)=lnx为可导函数,则f(x)在点x=1.01处的近似值为______.
0.01
[解析] 由f(x
0+Δx)≈f(x
0)+f'(x
0)Δx,故
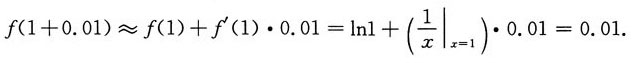
5. 若级数
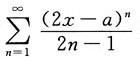
的收敛域为[3,4),则常数a=______.
7
[解析]
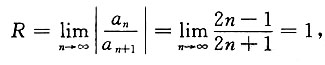
所以-1<2x-a<1.当2x-a=-1时,级数收敛;当2x-a=1时,级数发散,所以其收敛域为-1≤2x-a<1,即
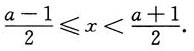
又级数收敛域为[3,4),所以
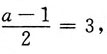
则a=7.
三、计算题1. 计算不定积分
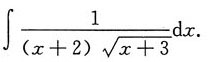
解:令
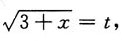
则x=t
2-3,dx=2tdt,
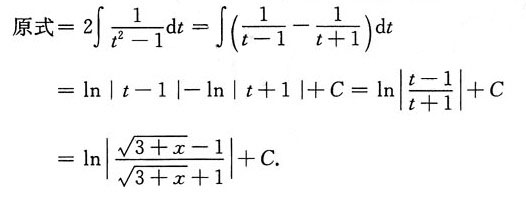
2. 设z是由方程x-mz=φ(y-nz)所确定的关于x,y的函数,证明:z满足方程
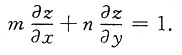
证明:先求
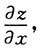
将方程x-mz=φ(y-nz)两边对x求偏导数,并注意到z是关于x,y的函数,得
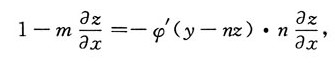
解得
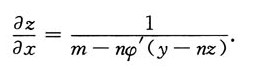
再将方程x-mz=φ(y-nz)两边对y求偏导数,得
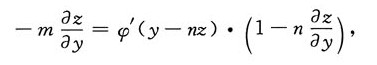
解得
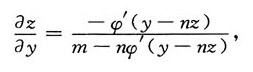
所以
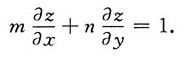
3. 求微分方程xy'-y=xlnx满足初始条件y|
x=e=e的特解.
解:将原方程改写成
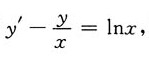
则
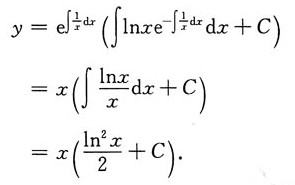
将初始条件y|
x=c=e代入得
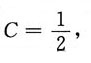
故原方程的特解为
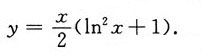
4. k取何值时,线性方程组
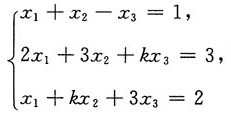
无解,有唯一解,有无穷解,当有解时,求出其全部解.
解:对方程组的增广矩阵施行初等行变换
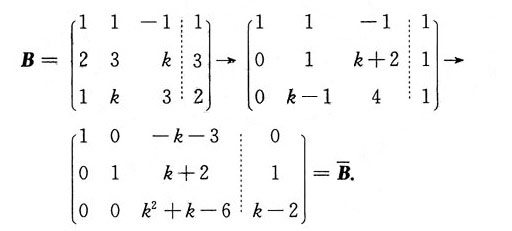
由
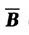
可知①当k=-3时,由于r(A)=2,r(B)=3故此方程组无解;
②当k=2时,r(A)=r(B)=2<3,此时原方程组有无穷多解,且由
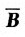
可知此时原方程组的同解方程组为
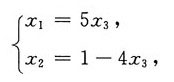
x
3为自由未知量,则原方程组通解为
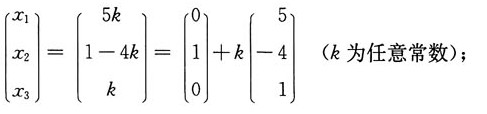
③当k≠-3且k≠2时,r(A)=r(B)=3,原方程组有唯一解,而且由
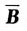
可知其唯一解为
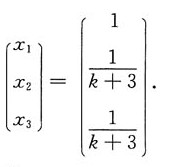
四、应用题(本题10分.将解答的主要过程、步骤和答案填写在相应位置上)1. 设需求函数为P+0.1Q=80,成本函数为C(Q)=5000+20Q,计算边际利润函数,并分别求Q=150,400时的边际利润.
解:利润=收益-成本.即
L(Q)=PQ-C(Q)=(80-0.1Q)Q-5000-20Q=60Q-0.1Q2-5000,
则边际利润函数为L'(Q)=-0.2Q+60.
当Q=150时,边际利润为30;
当Q=400时,边际利润为-20.