银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
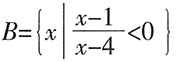 ,则A∩B=______。
,则A∩B=______。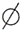
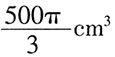
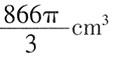
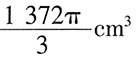
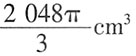
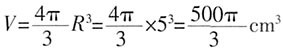 ,故选A。
,故选A。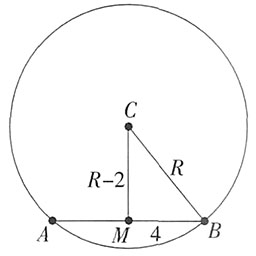
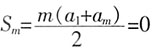 得a1=-2,所以am=-2+(m-1)×1=2,解得m=5,故选C。
得a1=-2,所以am=-2+(m-1)×1=2,解得m=5,故选C。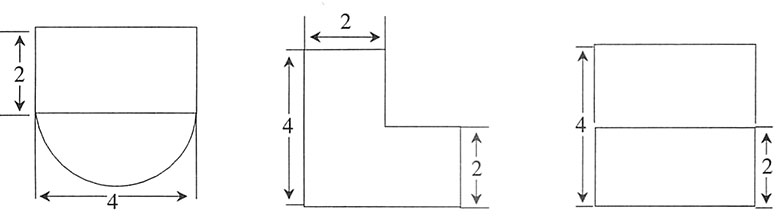
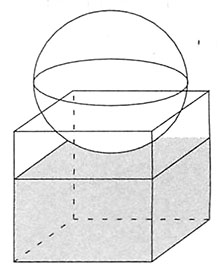
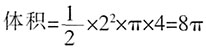 ,所以这个几何体的体积是16+8π;故选A。
,所以这个几何体的体积是16+8π;故选A。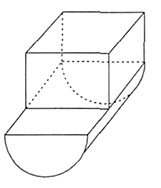
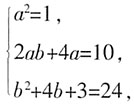 解得:a=-1,b=-7,或a=1,b=3,则5a-b=2。
解得:a=-1,b=-7,或a=1,b=3,则5a-b=2。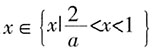 ;当0<a<2时,
;当0<a<2时,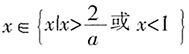 ,当a>2,
,当a>2,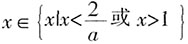 。
。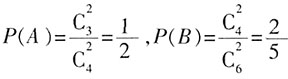 。故取出的4个球均为黑球的概率为
。故取出的4个球均为黑球的概率为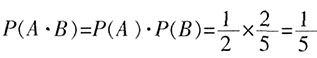 。
。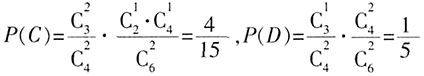 。故取出的4个球中恰有1个红球的概率为
。故取出的4个球中恰有1个红球的概率为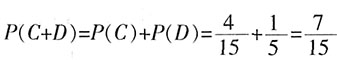 。
。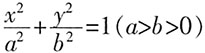 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60。
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60。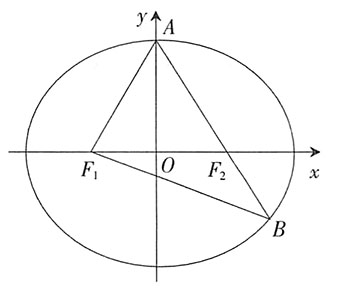
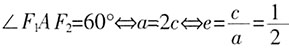
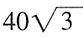 ,求a,b的值。
,求a,b的值。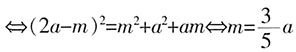
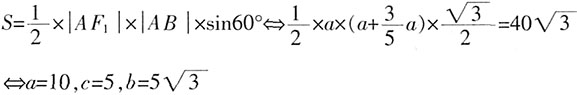
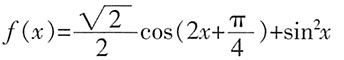
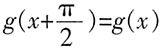 ,且当
,且当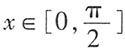 时,
时,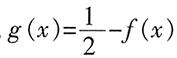 ;求函数g(x)在[-π,0]上的解析式。
;求函数g(x)在[-π,0]上的解析式。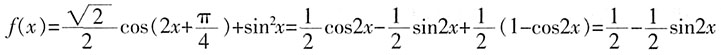
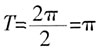
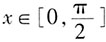 时,
时,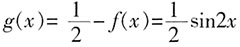
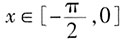 时,
时,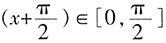
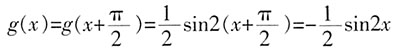
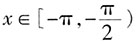 时,
时,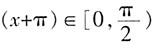 得:
得: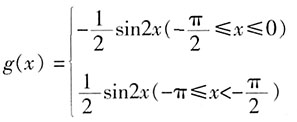
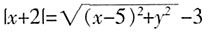 ,易知圆C2上的点位于直线x=-2的右侧,∴x+2>0,∴
,易知圆C2上的点位于直线x=-2的右侧,∴x+2>0,∴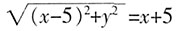 ,化简得曲线C1的方程为y2=20x。
,化简得曲线C1的方程为y2=20x。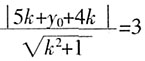 ,
,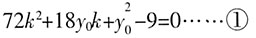
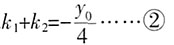
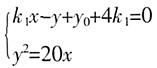 ,得k1y2-20y+20(y0+4k1)=0……③
,得k1y2-20y+20(y0+4k1)=0……③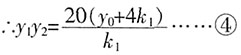 ,同理可得
,同理可得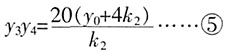
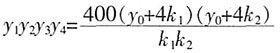
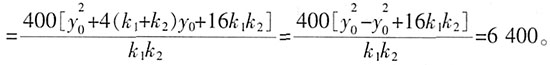
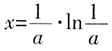 。
。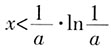 时,f'(x)<0,f(x)单调递减;
时,f'(x)<0,f(x)单调递减;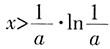 时,f'(x)>0,f(x)单调递增。
时,f'(x)>0,f(x)单调递增。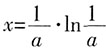 时,f(x)取最小值
时,f(x)取最小值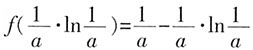 。
。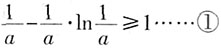
 ,即a=1时,①式成立。
,即a=1时,①式成立。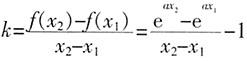 ,
,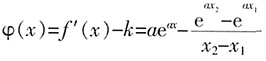 ,则
,则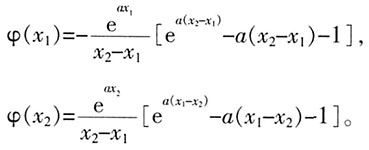
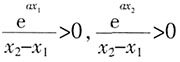 ,∴φ(x1)<0,φ(x2)>0,
,∴φ(x1)<0,φ(x2)>0,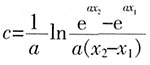 ,∴当且仅当
,∴当且仅当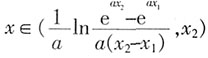 时,f'(x)>k。
时,f'(x)>k。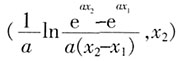 。
。