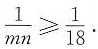问题求解1. a,b,c是非零实数,则代数式

的所有值的集合是______.
- A.{-4,-2,2,4}
- B.{-4,0,4}
- C.{-4,-2,0,4}
- D.{-3,0,2}
- E.以上答案均不正确
A B C D E
B
[解析] 利用
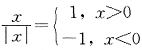
,分以下几种情况讨论:
(1)a,b,c三个数全为正数,
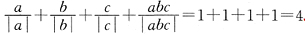
.
(2)a,b,c三个数两个正数一个负数,不妨设a>0,b>0,c<0,
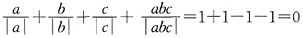
.
(3)a,b,c三个数两个负数一个正数,不妨设a<0,b<0,c>0,
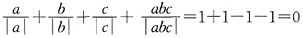
(4)a,b,c三个数全为负数,
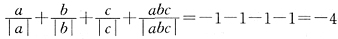
.
所以代数式
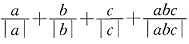
的所有值的集合是{-4,0,4}.故选B.
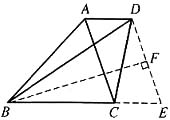
6. 如下图所示,在梯形ABCD中,AD//BC,AD=2,AC=4,BC=6,BD=8,则梯形ABCD的面积为______.
A.

B.
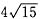
C.16
D.32
E.12
A B C D E
B
[解析] 如图所示,过D作DE//AC交BC的延长线于E点,如下图所示,S
△ABD=S
△DCE,所以S
梯形ABCD=S
△BDE,作BF⊥DE相交于F点,在等腰△BED中,
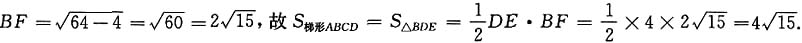
15. {a
n}是等差数列,S
10>0,S
11<0,则使a
n<0的最小的n=______.
A B C D E
B
[解析]


则a
5>0,a
6<0,则使a
n<0最小的n=6.
综上所述,答案选择B.
16. 如下图所示,在直角三角形ABC中,AC=4,BC=3,DE∥BC,已知梯形BCED的面积为3,则DE的长为______。
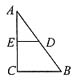
A.
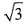
B.
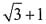
C.
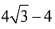
D.
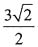
E.

A B C D E
D
S
△ABC=
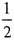
BC·AC=
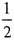
×3×4=6,且S
梯BCED=3,即S
△ABC=3,又∵△ABC相似于△AED,

。
(1)知识点:平面几何问题。
(2)注意事项:相似三角形面积比等于相似比的平方。
22. 方程
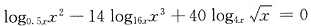
的解为______.
A.1
B.4
C.0或
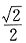
D.1或4
E.1或4或
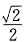
A B C D E
E
[解析] 由换底公式
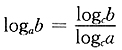
,原方程可变为:
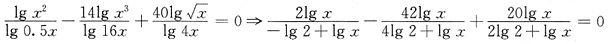
令y=lgx,则上式变为
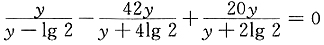
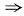
-10y[2y
2-(31g2)y-2(1g2)
2]=0
解得y=0或y=2lg2或
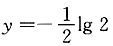
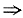
lgx=0或lgx=2lg2或
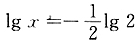
,所以x=1或4或

.
故选E.
23. 若x
3+x
2+ax+b能被x
2-3x+2整除,则______.
- A.a=4,b=4
- B.a=-4,b=-4
- C.a=10,b=-8
- D.a=-10,b=8
- E.a=-2,b=0
A B C D E
D
[解析] 令f(x)=x
3+x
2+ax+b,当x
2-3x+2=0时,x=1或2.由整除的性质知1和2是x
3+x
2+ax+b=0的两个根.即
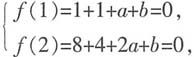
解得a=-10,b=8.
25. 当m为何值时,(m+2)x+3my+1=0与(m-2)x+(m+2)y-3=0相互垂直______.
A.

B.m=-2
C.m=2
D.

E.

A B C D E
D
[解析] 直线ax+by+c=0与bx-ay+c=0互相垂直.
则(m+2)(m-2)+3m(m+2)=0,即2m
2+3m-2=0,解得

或-2.
综上所述,答案选择D.
26. 已知x
2+(2k+1)x+k
2-2=0的两个实数根的平方和等于11,则k=______.
- A.k=-3或1
- B.k=-3
- C.k=1
- D.k=3
- E.k=2
A B C D E
C
[解析] 因为x
1+x
2=-(2k+1),

所以(2k+1)
2-2(k
2-2)=11,即k
2+2k-3=0,(k+3)(k-1)=0,所以k
1=1,k
2=-3,但Δ≥0,(2k+1)
2-4(k
2-2)≥0
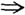
4k≥-9,所以
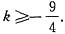
取k=1.
27. 如果a、b是质数,且a
2-13a+m=0,b
2-13b+m=0,则

的值为______.
A.

B.

C.

D.

E.

A B C D E
C
[解析] 方法:利用根与系数关系.
a
3-13a+m=0,b
2-13b+m=0,a,b为质数,分情况讨论,
(1)a=b时,a,b为方程x
2-13x+m=0的一个根,a=b=2或a=b=11,所以

(2)a≠b时,a,b为方程x
2-13x+m=0的两个不等质数根,a+b=13=2+11,ab=2×11=22,或a=2,b=11;a=11,b=2,代入

29. 已知正项等比数列{a
n}满足:a
7=a
6+2a
5,若存在两项a
m,a
n使得
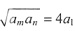
,则
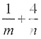
的最小值为______
A.
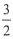
B.
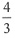
C.
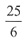
D.
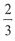
E.以上答案均不正确
A B C D E
A
[解析] 由a
7=a
6+2a
5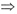
a
5q
2=a
5q+2a
5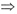
q
2-q-2=0
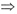
q=2,
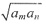
=4a
1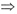
a
ma
n=16a
12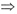
a
1q
m-1a
1q
n-1=16(a
1)
2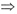
m+n=6
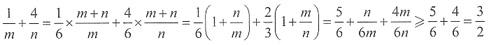
[考点] 等比数列和平均值定理。
32. 已知等式

成立,则
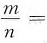
______.
A.1
B.

C.
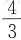
D.2
E.
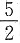
A B C D E
B
[解析] 有理数与无理数的运算
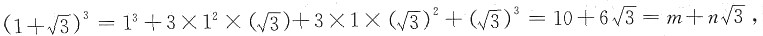
故
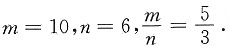
33. 已知直线ax-by+3=0(a>0,b>0)过圆x
2+4x+y
2-2y+1=0的圆心,则ab的最大值为______.
A.
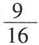
B.
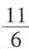
C.
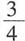
D.
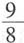
E.
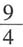
A B C D E
D
[解析] 由圆的方程可知,圆心为(-2,1),因为直线经过圆心,因此将圆心坐标代入直线方程,则-2a-b+3=0,即2a+b=3,由均值不等式可知,(2a+b)
2≥4·2a·b=8ab,即
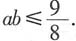
 的所有值的集合是______.
的所有值的集合是______.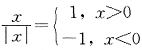 ,分以下几种情况讨论:
,分以下几种情况讨论: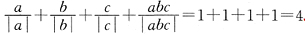 .
.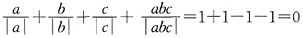 .
.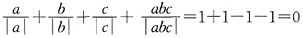
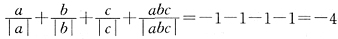 .
.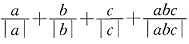 的所有值的集合是{-4,0,4}.故选B.
的所有值的集合是{-4,0,4}.故选B.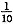 ,乙的工作效率为
,乙的工作效率为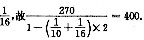
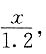 若记女生人数为a,则男生人数为1.8a,则全班测验的总分为2.8a×75,得
若记女生人数为a,则男生人数为1.8a,则全班测验的总分为2.8a×75,得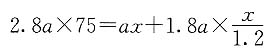
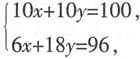 解得
解得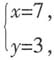 即甲公司每周工时费为7万元,故答案为B.
即甲公司每周工时费为7万元,故答案为B.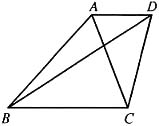

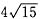
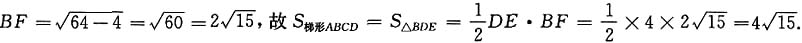
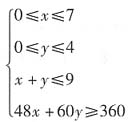 公司总成本为Z=160x+252y满足约束条件的可行域如图所示:
公司总成本为Z=160x+252y满足约束条件的可行域如图所示: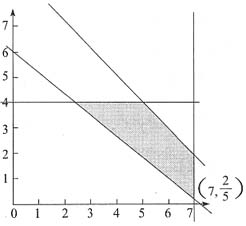
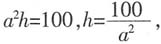 总的造价为
总的造价为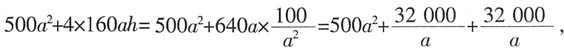 根据均值不等式,当
根据均值不等式,当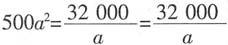 时,上式取得最小值,此时a=4.
时,上式取得最小值,此时a=4.
 设甲、乙两地相距S公里,两车第一次相遇于距甲地20公里处,第二次相遇于距乙地10公里处,则
设甲、乙两地相距S公里,两车第一次相遇于距甲地20公里处,第二次相遇于距乙地10公里处,则 S(S-50)=0,所以S=50.
S(S-50)=0,所以S=50.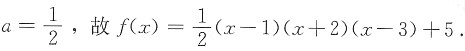
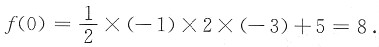
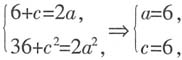 因此选E.
因此选E.


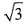
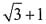
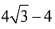
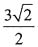

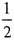 BC·AC=
BC·AC=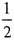 ×3×4=6,且S梯BCED=3,即S△ABC=3,又∵△ABC相似于△AED,
×3×4=6,且S梯BCED=3,即S△ABC=3,又∵△ABC相似于△AED, 。
。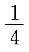



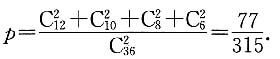

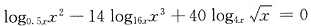 的解为______.
的解为______.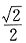
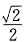
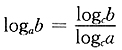 ,原方程可变为:
,原方程可变为: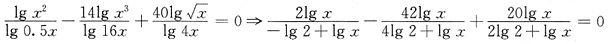
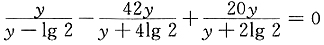
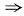 -10y[2y2-(31g2)y-2(1g2)2]=0
-10y[2y2-(31g2)y-2(1g2)2]=0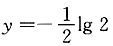
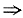 lgx=0或lgx=2lg2或
lgx=0或lgx=2lg2或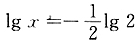 ,所以x=1或4或
,所以x=1或4或 .
.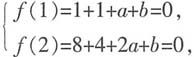 解得a=-10,b=8.
解得a=-10,b=8.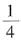

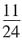
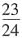
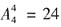 种,不对应取法有9种,所以不对应取球的概率
种,不对应取法有9种,所以不对应取球的概率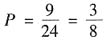 ,应选B。
,应选B。


 或-2.
或-2. 所以(2k+1)2-2(k2-2)=11,即k2+2k-3=0,(k+3)(k-1)=0,所以k1=1,k2=-3,但Δ≥0,(2k+1)2-4(k2-2)≥0
所以(2k+1)2-2(k2-2)=11,即k2+2k-3=0,(k+3)(k-1)=0,所以k1=1,k2=-3,但Δ≥0,(2k+1)2-4(k2-2)≥0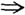 4k≥-9,所以
4k≥-9,所以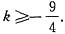 取k=1.
取k=1. 的值为______.
的值为______.






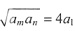 ,则
,则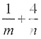 的最小值为______
的最小值为______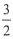
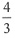
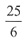
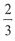
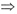 a5q2=a5q+2a5
a5q2=a5q+2a5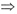 q2-q-2=0
q2-q-2=0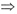 q=2,
q=2,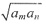 =4a1
=4a1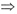
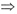 a1qm-1a1qn-1=16(a1)2
a1qm-1a1qn-1=16(a1)2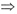 m+n=6
m+n=6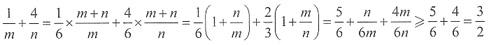
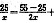 1,解得x=10.
1,解得x=10. 成立,则
成立,则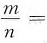 ______.
______.
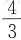
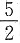
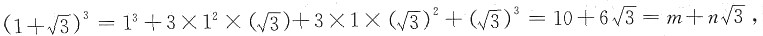
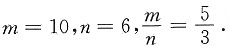
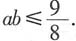
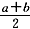 元的价格出售.在这次买卖中,张师傅是______.
元的价格出售.在这次买卖中,张师傅是______.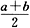 -20a+30×
-20a+30×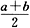 -30b=5a-5b.
-30b=5a-5b.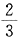 去挖树坑,余下人数的
去挖树坑,余下人数的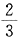 运树苗,最后余下的4名同学负责供应开水,则这个班共有学生 人.
运树苗,最后余下的4名同学负责供应开水,则这个班共有学生 人.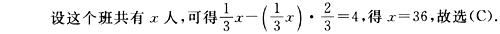
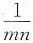 的最小值为______.
的最小值为______.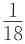
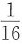
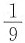
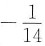
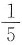
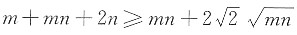 ,则有
,则有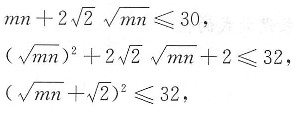
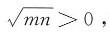 解得
解得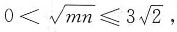 故
故