问题求解3. 4个不同的小球放入甲、乙、丙、丁4个盒中,恰有一个空盒的方法有______种。
A.
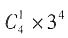
B.

C.
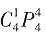
D.
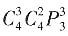
E.以上结论均不正确
A B C D E
D
[解析] 捆绑法。先从4个不同的小球中任意拿出2个,即
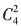
,将其捆绑看成一个整体,再与剩下的2个球放入甲、乙、丙、丁4个盒中的任意3个,即
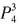
,共有方法
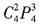
,应选D。
12. 已知数列{a
n}的前n项的和S
n=1-m
2a
n,则此数列是______.
A.以
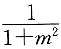
为首项,公差为
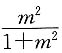
的等差数列
B.以
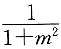
为首项,公比为
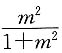
的等比数列
C.以
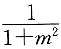
为首项,公差为
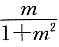
的等差数列
D.以
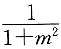
为首项,公比为
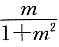
的等比数列
E.既非等差数列,亦非等比数列
A B C D E
B
[解析] 由题意,有S
1=a
1=1-m
2a
1,由此可得数列的首项
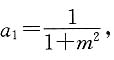
又S
n=a
n+S
n-1=a
n+(1-m
2a
n-1).所以
a
n+(1-m
2a
n-1)=1-m
2a
n 化简得a
n:a
n-1=m
2:(1+m
2).
故本题应选B.
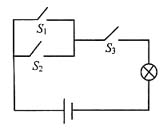
16. 下图是一个简单的电路,S
1、S
2、S
3表示开关,则闭合S
1、S
2、S
3中的两个,灯泡发光的概率是______。
A.
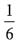
B.
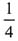
C.
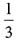
D.
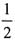
E.
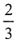
A B C D E
E
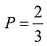
。
(1)知识点:古典概型问题。
(2)注意事项:要看清题说的是闭合三个开关中的两个,所以总数是三种情况。
17. 已知关于x的一元二次方程x
2+2(m+1)x+(3m
2+4mn+4n
2+2)=0有实根,则m,n的值为______.
A.m=-1,
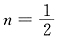
B.
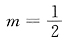
,n=-1
C.
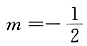
,n=1
D.m=1,
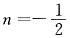
E.以上答案均不正确
A B C D E
D
[解析] 因为方程有实根,
所以Δ=b
2-4ac=[2(m+1)]
2-4×(3m
2+4mn+4n
2+2)≥0.
化简,得:-4(2m
2-2m+4mn+4n
2+1)≥0,即2m
2-2m+4mn+4n
2+1≤0.
分解因式,得(m+2n)
2+(m-1)
2≤0
因为(m+2n)
2≥0,(m-1)
2≥0,所以有
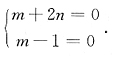
所以m=1,
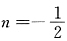
.故选D.
18. 四边形A
1B
1C
1D
1是平行四边形,A
2,B
2,C
2,D
2分别是A
1B
1C
1D
1四边的中点,A
3,B
3,C
3,D
3分别是A
2B
2C
2D
2四边的中点,以此类推,得到四边形序列A
nB
nC
nD
n(n=1,2,3,…)。设A
nB
nC
nD
n面积为S
n,且S
1=12,则S
1+S
2+S
3+…=______
A B C D E
C
[解析] 通过分析可知后一个四边形的面积是前一个四边形面积的
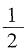
,故
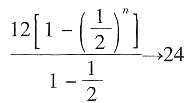
。
[考点] 等比数列和平面几何问题。
20. 在伯努利试验中,事件A出现的概率是

,则在此3重伯努利试验中,事件A出现奇数次的概率是______.
A.

B.

C.

D.

E.

A B C D E
C
[解析]

.
综上所述,答案选择C.
22. 如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可选择,则不同的着色方法共有______种.
A B C D E
B
[解析] 解法一:按区域分
(1)2、4同色,(2)2、4异色,
所以N=4×3×2(1×2+1×1)=24×3=72.
解法二:按颜色分
(1)4种颜色:2、4同色或3、5同色,

;
(2)3种颜色:2、4同色且3、5同色,

.
所以N=48+24=72.
23. 设{a
n}是公差不为0的等差数列,a
1=2且a
1,a
3,a
6成等比数列,则{a
n}的前n项和S
n=______。
A.
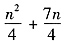
B.
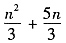
C.
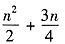
D.n
2+n
E.以上答案均不正确
A B C D E
A
[解析] a
1,a
3,a
6成等比数列,则a
32=a
1a
6即(a
1+2d)
2=a
1(a
1+5d),解得
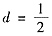
或d=0(舍去),所以{a
n}的前n项和
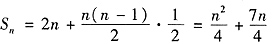
,应选A。
30. 已知a
2+4a+1=0且
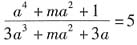
,则m=______。
A.

B.
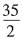
C.
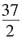
D.
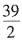
E.
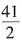
A B C D E
C
[解析] a
4+ma
2+1=15a
3+5ma
2+15a,整理得a
4-4ma
2-15(a
2+1)+1=0,因为a
2+4a+1=0,所以a
4-4ma
2+60a
2+1=0,又(a
2+1)
2=16a
2,即a
4-14a
2+1=0,所以60-4m=-14,
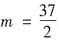
,应选C。
32. 某公司投资一个项目,已知上半年完成了预算的
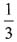
,下半年完成了剩余部分的
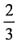
,此时还有8000万元投资未完成,则该项目的预算为______。
- A.3亿元
- B.3.6亿元
- C.3.9亿元
- D.4.5亿元
- E.5.1亿元
A B C D E
B
[解析] 设该项目的预算为x元,则剩余部分的
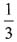
即为8000万元
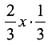
=8×10
7 解出:x=3.6×10
8=3.6亿元
(1)知识点:本题考查了比例应用问题。
(2)注意事项:应用题中常用的技巧,把文字语言转化为数学符号语言,剩余的8000万元投资即为下半年未完成的部分。
35. 已知a
1,a
2,a
3,…是各项为正数的等比数列,a
6=a
4=24,a
1a
7=64,则其前8项的和等于______.
A B C D E
B
[解析]
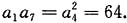
因为a
n>0,所以a
4=8,a
6=a
4+24=32,又a
6=a
4q
2,所以
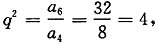
所以q=2.a
1a
7=64,即a
1·a
1q
6=64,所以

所以a
1=1.即a
n=2
n-1(n∈N*),
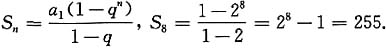
 综上所述,答案选择A.
综上所述,答案选择A.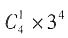

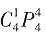
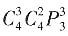
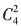 ,将其捆绑看成一个整体,再与剩下的2个球放入甲、乙、丙、丁4个盒中的任意3个,即
,将其捆绑看成一个整体,再与剩下的2个球放入甲、乙、丙、丁4个盒中的任意3个,即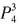 ,共有方法
,共有方法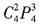 ,应选D。
,应选D。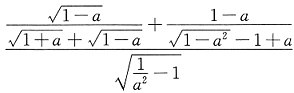 (0<n<1)得______.
(0<n<1)得______.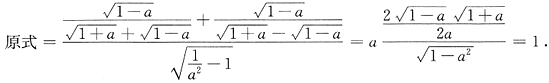
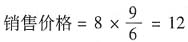 ,又从进货量的百分比与销售价格成反比例可得:
,又从进货量的百分比与销售价格成反比例可得: ,应选C。
,应选C。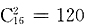 种分配方案.故选B.
种分配方案.故选B.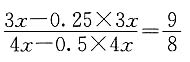

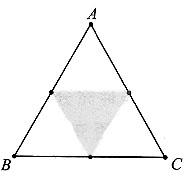
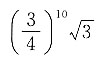
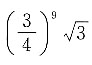
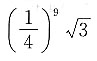
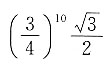
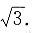 每次按题目中的方式操作后,正三角形的面积会剩余原来的
每次按题目中的方式操作后,正三角形的面积会剩余原来的 ,那么10次过后,其面积为
,那么10次过后,其面积为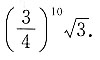
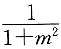 为首项,公差为
为首项,公差为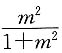 的等差数列
的等差数列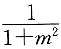 为首项,公比为
为首项,公比为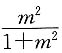 的等比数列
的等比数列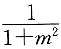 为首项,公差为
为首项,公差为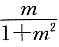 的等差数列
的等差数列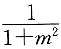 为首项,公比为
为首项,公比为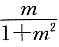 的等比数列
的等比数列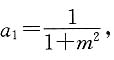 又Sn=an+Sn-1=an+(1-m2an-1).所以
又Sn=an+Sn-1=an+(1-m2an-1).所以 ,其中x为整数,且|x|≤3,则a=______.
,其中x为整数,且|x|≤3,则a=______. ,故x>1或x<-7,又x为整数且|x|≤3,
,故x>1或x<-7,又x为整数且|x|≤3, 分别为______
分别为______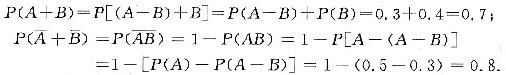

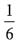
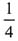
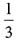
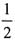
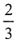
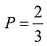 。
。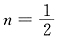
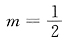 ,n=-1
,n=-1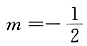 ,n=1
,n=1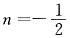
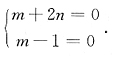
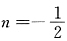 .故选D.
.故选D.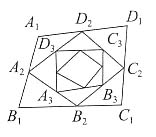
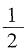 ,故
,故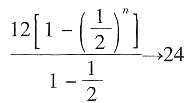 。
。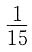
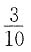
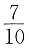
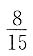
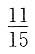
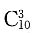 .而3个空车位恰好是连接在一起的情形,只有(1 2 3),(2 3 4),(3 4 5),…,(8 9 10)共8个.所以,所求概率为
.而3个空车位恰好是连接在一起的情形,只有(1 2 3),(2 3 4),(3 4 5),…,(8 9 10)共8个.所以,所求概率为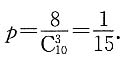
 ,则在此3重伯努利试验中,事件A出现奇数次的概率是______.
,则在此3重伯努利试验中,事件A出现奇数次的概率是______.




 .
.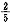 ,那么甲、乙、丙共有的存款数额是 元.
,那么甲、乙、丙共有的存款数额是 元.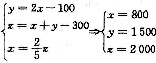 .
.
 ;
; .
.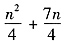
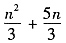
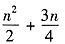
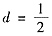 或d=0(舍去),所以{an}的前n项和
或d=0(舍去),所以{an}的前n项和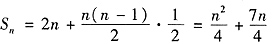 ,应选A。
,应选A。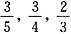 来装配若干台机器,那么原来存有丙种部件______件.
来装配若干台机器,那么原来存有丙种部件______件.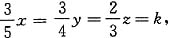 所以
所以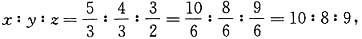 所以有丙种部件:
所以有丙种部件: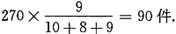
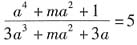 ,则m=______。
,则m=______。
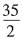
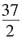
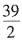
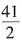
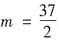 ,应选C。
,应选C。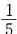 调到甲部门,那么两个部门的人数相等.该公司的总人数为______.
调到甲部门,那么两个部门的人数相等.该公司的总人数为______.
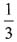 ,下半年完成了剩余部分的
,下半年完成了剩余部分的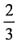 ,此时还有8000万元投资未完成,则该项目的预算为______。
,此时还有8000万元投资未完成,则该项目的预算为______。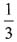 即为8000万元
即为8000万元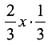 =8×107 解出:x=3.6×108=3.6亿元
=8×107 解出:x=3.6×108=3.6亿元
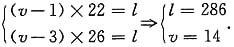
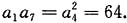 因为an>0,所以a4=8,a6=a4+24=32,又a6=a4q2,所以
因为an>0,所以a4=8,a6=a4+24=32,又a6=a4q2,所以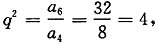 所以q=2.a1a7=64,即a1·a1q6=64,所以
所以q=2.a1a7=64,即a1·a1q6=64,所以 所以a1=1.即an=2n-1(n∈N*),
所以a1=1.即an=2n-1(n∈N*),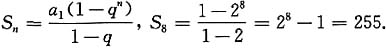

 ,OD=16,设AO=x,则
,OD=16,设AO=x,则

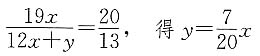
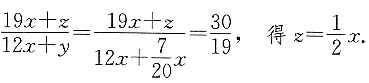
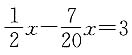

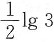
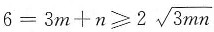 ,解得mn≤3,故lgm+lgn=lgmn≤lg3.
,解得mn≤3,故lgm+lgn=lgmn≤lg3.