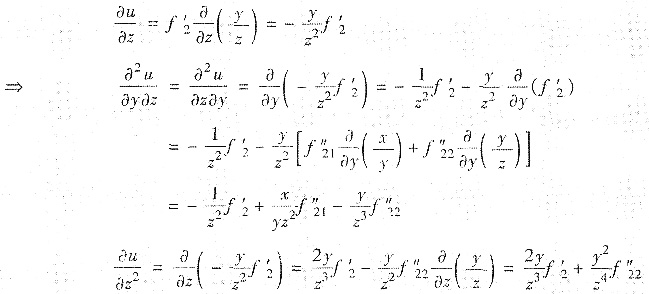一、选择题3. 设
______
A．
B．
C．
D．
A B C D
C
[解析] 由
选C．
4.
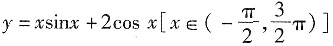
的拐点坐标是______
A．
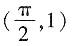
B．(0，2)
C．(π，-2)
D．
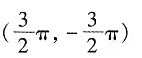
A B C D
B
[解析] y'=sinx+xcosx-2sinx，y"=-xsinx，令y"=0得x=0，x=π，又因为y'''=-sinx-xcosx，将上述两点代入y"(π)≠0，所以(π，-2)是拐点．
5. 曲线
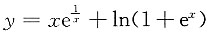
的渐近线有______
- A.1条水平的，1条斜的，1条铅直的．
- B.2条水平的，没有斜的，1条铅直的．
- C.没有水平的，2条斜的，1条铅直的．
- D.1条水平的，1条斜的，没有铅直的．
A B C D
C
[解析] 因
，
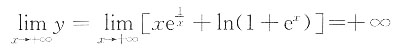
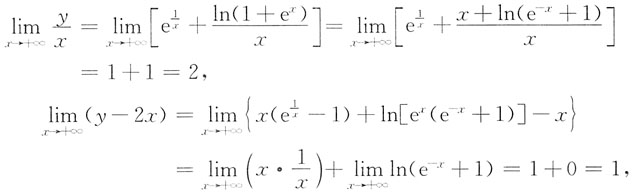
所以有1条斜渐近线y=2x+1(沿x→+∞方向)．
又
所以又有1条斜渐近线y=x+1(沿x→-∞方向)．
综上，曲线左右各有一条斜渐近线，所以就没有水平渐近线．
又
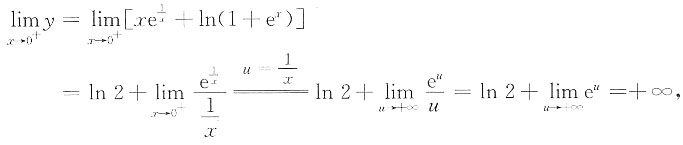
所以有1条铅直渐近线．选C．
6. 设函数f(x)连续，则在下列变上限积分定义的函数中，必为偶函数的是______
A．
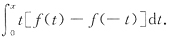
B．
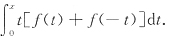
C．
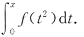
D．
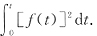
A B C D
B
[解析] 已知若g(x)在[-a，a]连续为奇函数，则|g(t)dt一定是偶函数．在这四个选项中，函数g(x)=x[f(x)+f(-x)]满足
g(-x)=-x[f(-x)+f(x)]=-g(x)
为奇函数．因此选B．
取f(x)=x，则相应的
A项
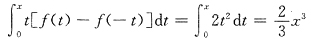
C项
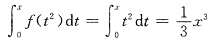
D项
均为奇函数，故不能选A，C，D．因此，应选B．
7. 设A是m×n阶矩阵，下列命题正确的是______．
- A.若方程组AX=0只有零解，则方程组AX=b有唯一解
- B.若方程组AX=0有非零解，则方程组AX=b有无穷多个解
- C.若方程组AX=b无解，则方程组AX=0一定有非零解
- D.若方程组AX=b有无穷多个解，则方程组AX=0一定有非零解
A B C D
D
[解析] 方程组
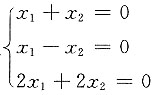
只有零解，而
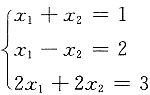
无解，故A不对；
方程组
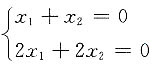
有非零解，而
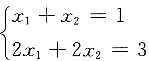
无解，故B不对；
方程组
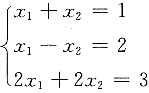
无解，但
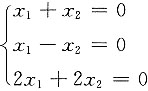
只有零解，故C不对；
若AX=b有无穷多个解，则
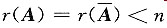
，从而r(A)＜n，故方程组AX=0一定有非零解，选D．
8. 设
则f'(1)=______
A．
B．
C．
D．
A B C D
B
[解析]
选B．
二、填空题1. 曲线
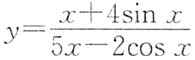
的水平渐近线方程为______．
2. 设
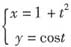
，则
=______．
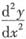
[考点] 含有参数的复合函数求导数
[解析] 由参数式求导公式得
，
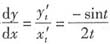
再对x求导，由复合函数求导法得
3. 设函数
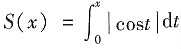
。则
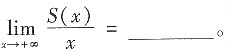
[考点] 本题考查的是极限的夹逼准则。先求出S(x)的范围，然后利用极限的夹逼准则即可得到结果。
[解析] 对于任意的x∈(nπ，(n+1)π)，有
而
所以
当n→∞时，x→+∞，所以由极限的夹逼准则有
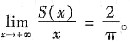
4. 设
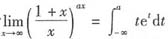
，则a=______．
2
[考点] 函数的极限、广义积分
[解析] 可得
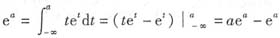
，所以a=2．
5. f(sinx)=cos2x+3x+2，则f'(x)=______．
[解析] 由f(sinx)=cos2x+3x+2，得f(sinx)=1-2sin
2x+3x+2，
f(x)=1-2x
2+3arcsinx+2，
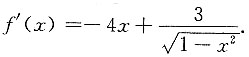
6. 设
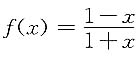
，则f
(n)(x)=______．
三、解答题1. 设f(x)在[a，b]上连续，在(a，b)内可导(a＞0)，证明：存在ξ∈(a，b)，使得
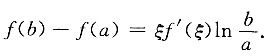
证明：令F(x)=lnx，
，
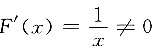
由柯西中值定理，存在ξ∈(a，b)，使得
，
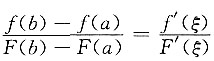
即
，整理得
．
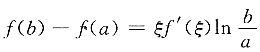
2. 计算二重积分
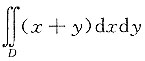
，其中D：x
2+y
2≤x+y+1．
解：令
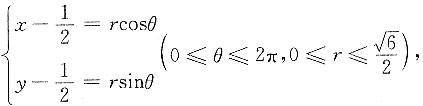
则
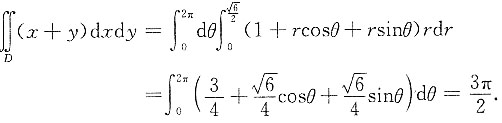
3. 求f(x)的表达式；
解法1 联立
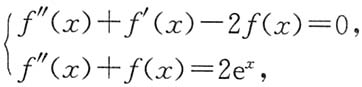
解得f'(x)-3f(x)=-2e
x，因此
f(x)=e
3∫dx[∫(-2e
x)e
-3∫dxdx+C]
=e
3x(-2∫e
xe
-3xdx+C)=e
x+Ce
3x，
将其代入f"(x)+f(x)=2e
x，有
(e
x+9Ce
3x)+e
x+Ce
3x=2e
x，
可得C=0，于是f(x)=e
x．
解法2 f"(x)+f'(x)-2f(x)=0对应的特征方程是λ
2+λ-2=0，其根为λ
1=1，λ
2=-2，故f"(x)+f'(x)-2f(x)=0的通解为f(x)=C
1e
x+C
2e
-2x，且
f'(x)=C
1e
x-2C
2e
-2x，f"(x)=C
1e
x+4C
2e
-2x，
代入f"(x)+f(x)=2e
x，有
(C
1e
x+4C
2e
-2x)+C
1e
x+C
2e
-2x=2e
x，
从而知C
1=1，C
2=0，即有f(x)=e
x．
4. 求曲线
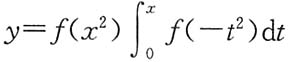
的拐点．
解：
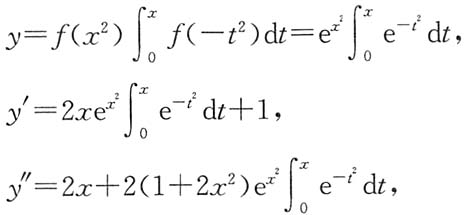
因为当x＜0时，y"＜0；当x＞0时，y"＞0，又y(0)=0，所以曲线的拐点为(0，y(0))，即点(0，0)．
5. 计算二重积分
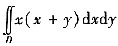
，其中D={(x，y)|x
2+y
2≤2，y≥x
2}。
解：根据对称性可知
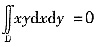
，所以有
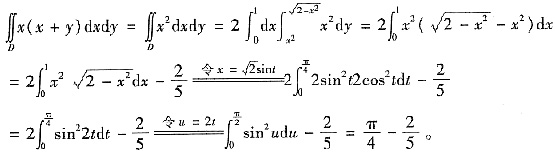
[考点] 二重积分的计算。
6. 求初值问题
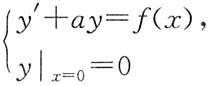
的解y(x)，其中a是正常数；
证明：原方程的通解为
y(x)=e
-∫adx[∫f(x)e
∫adxdx+C]=e
-ax[∫f(x)e
axdx+C]=e
-ax[F(x)+C]，
其中F(x)是f(x)e
ax的任一原函数．由y(0)=0，得C=-F(0)，故
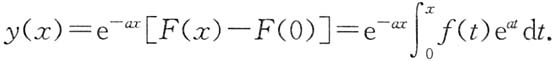
7. 若|f(x)|≤k(k为常数)，证明当x≥0时，有
．
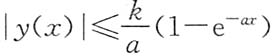
证明：
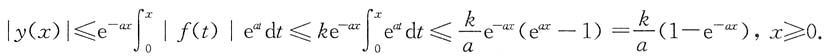
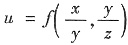，其中f(s，t)有连续的二阶偏导数．8. 求du．
解：由一阶全微分形式不变性及全微分四则运算法则，得
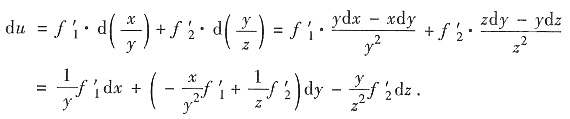
9. 求
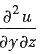
解：由du中dy，dz的系数分别得
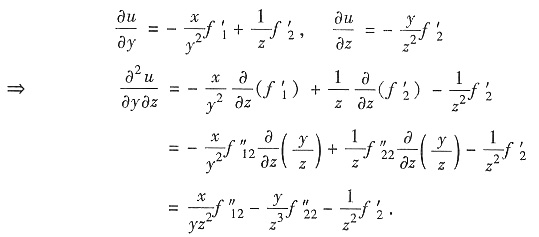
该题有如下式:设
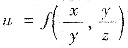
，其中f(s,t)有连续的二阶偏导数，求
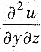
与
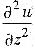
为了求
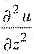
，必须先求
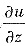
.为了求
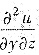
必须先求
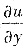
或
(混合偏导数连续时与求导次序无关).因此我们先求
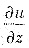
由复合函数求导法得
由于B2-AC＞0，函数u(x，y)不存在无条件极值，所以D的内部没有极值，故最大值与最小值都不会在D的内部出现．但是u(x，y)连续，所以，在平面有界闭区域D上必有最大值与最小值，故最大值点和最小值点必定都在D的边界上．
．
．
深色：已答题 浅色：未答题